InterviewSolution
Saved Bookmarks
| 1. |
Derivesigma=("ne"^2 tau)/m, where the symbols have their usual meaning. |
|
Answer» Solution :Let .n. be the numberdensityof electrons , .L. be the lengthof the CONDUCTORA and .A.be the areaof cross -sectionof the conductor . Let `v_d` be the drift VELOCITYOF the electrons and Dx be a small length . Electrons drift in a directionoppositeto the electric field. Number ofelectronsin .Dx.and area of cross -section .A.is equal to (ADx) n. Charge on the theseelectrons =(nADx)e. If Dt is the time taken for effectivedisplacementof electronsthen rate of flow charge = `nAe ((Deltax)/(Deltat))` . By DEFINITION,electric current I=rate of flowof charge i.e.,`I=nAev_d`...(1) where , average velocityof electrons with whichit drifts againstthe directionof electric field is known as drift velocity`(v_d)`. Let .a. be the accelerationof electrons. Let .E.be the electricfieldintensity . Force on electrons, F=ma i.e., eE=ma But = `a=v_dt` where .t.is the relaxationtime . Relaxationtime representsthe average timetaken for two successivecollisionsof electronsand ionsin the lattice. 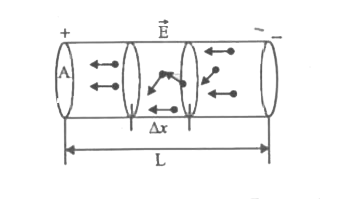 Hence ,`eE=mv_dt` or `v_d=(eE)/(mtau)` ...(2) We alsoknow that electricpotentialdifferencebetween the ends of the conductorV=EL `v_d =(eV)/(mtauL)` substitutingthis is the expression (1) We write, `I=nAe ((eV)/(mtauL))` i.e., `I=((nAe^2)/(mtauL))V` `R=(mtau L)/(nAe^2)`is called the electricalresistanceof a conductor . and `K=((nAe^2)/(mtauL))` is called the electric conductance of a conductor . the expression `sigma =("NE"^2)/(mtau)` is called the electricalconductivityand `1/sigma=(mtau)/("ne"^2)` is called electricalresistivity . |
|