Saved Bookmarks
| 1. |
Explain about the geometrical isomerism of octahedral complexes with suitable example. |
Answer» Solution :`(i)` Octahedral COMPLEXES of the type `[MA_(2)B_(4)]^(n+-)`, `[M(x x)_(2)B_(2)]^(n+-)` SHOWS cis-trans isomerism. Hence A and B are monodentate ligands and `x x` is bidentate ligand with two same kindof donor atoms. In the octahedral complex, the position of ligands is indicated by the following numbering scheme. 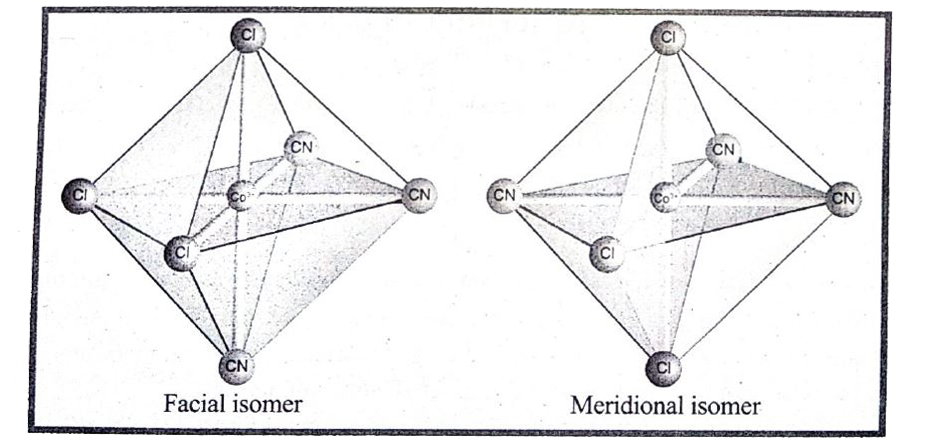 `(ii)` The POSITIONS `(1,2)(1,3)(1,4)(1,5),(2,3)(2,5)(2,6),(3,4)(3,6),(4,5)(4,6)` and `(5,6)` are identical and if two similar groups are present in any one of these positions, the isomer is referred as a cis-isomer. `(III)` Similarly positions `(1,6),(2,4)` and `(3,5)` are identical and if similar groups (or) ligands are present in these positions it is referred as a trans-isomer. `(iv)` Octahedral complex of the type `[MA_(3)B_(3)]^(n+-)` also shows geometrical isomerism. If thethree similar ligands (A) are present in the cornersof one TRIANGULAR face of the octahedronand the other `3` ligands (B) are present in the opposite triangular face, then the isomer is referred as a facial isomer (fac isomer). `(v)` If the three similar ligands are present around the meridian which is an imaginary semicircle from one apex of the octahedral to the opposite apex, the isomer is called a meridional isomer (mer is omer). This is called a meridional because each set of ligands can be regarded as lying on a meridian of an octahedran. |
|