Saved Bookmarks
| 1. |
Explain the dual behaviour of matter. Discuss its significance to microscopic particles like electrons. |
|
Answer» Solution :de - Broglie's hypothesis :The light is found to exhibit wave nature as well as particle nature (dual nature ) . Based on this idea of ' duel nature of light '. De Broglie in 1924 proposed that " all micro -particles including the electron moving with high velcoity are as sociated with dual nature (i.e., ) both particle wave nature . De- broglie an expression for the wavelength of the moving electron . Expression for de-Broglie wavelengths : According to 'Planck's quantum theory' , ENERGY of a photon , `E=hupsilon, " But " upsilon=(c)/(lamda)` `thereforeE=h.(c)/(lamda)......(1)` Einstein's mass - energy equivalence equation is `E=mc^(2)"".......(2)` combining eqns. (1) and (2) , `(h.c)/(lamda)=mc^(2)" or " lamda=(h)/(mc)=(h)/(p)` (p=mc=momentum) This equations is applicable to photons as well as to all microparticles , moving with high speed . `therefore` We can write in general, `lamda=(h)/(p)=(h)/(mv)` where m = mass of the microparticle and v = its velocity `lamda` , is called , de-Broglie wavelength or material wavelength . Significance of de - Broglie's CONCEPT: According to Bohr's theory , electron revolves in an ORBIT in which its angular momentum (mvr) is an integral multiple of`(h)/(2pi) ` . Bohr assumed electron as a particle . Hence his equation can be taken as `"mvr"=n((h)/(2pi))` where n = a whole number . According de Broglie , electron behaves as a standing (or stationary ) wave which extends round the nucleus in a circular orbit . If the ends of the electron wave meet to give a regular series of crests and troughs , the electron - wave is said to be 'in phase' . It means , there is constructive INTERFERNCE of electron waves and the electron motion has a character of standing wave or non-energy radiating motion . Always it is a necessary condition motion . Always it is a necessary condition to get an electron-wave in phase'such that the circumference fo the Bohr's orbit `(=2pir)` is equal to the whole number of multiple of the wavelength`(lamda)` of the electron -wave . `nlamda=2pir` `lamda=(2pir)/(n)` But`lamda=(h)/("mv")` (de-Broglie) `therefore(2pir)/(n) = (h)/("mv") "ormvr"=(nh)/(2pi)` 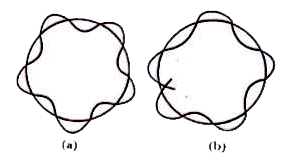 (a) Wave in - phase(b) Wave out -of phase This is Bohr's equation which stipulates that "the angular momentum of an electron moving round the nuclecus is an integral multiple of`(h)/(2pi)`" . This shows that, de-Broglie's theory and Bohr's theory are in agreement with each other . |
|