Saved Bookmarks
| 1. |
Find the equivalent capacitance between A and B (a) (b) . |
Answer» Solution :(a) By Kirchoff's rules (same procedure as in FINDING equivalent resistance) 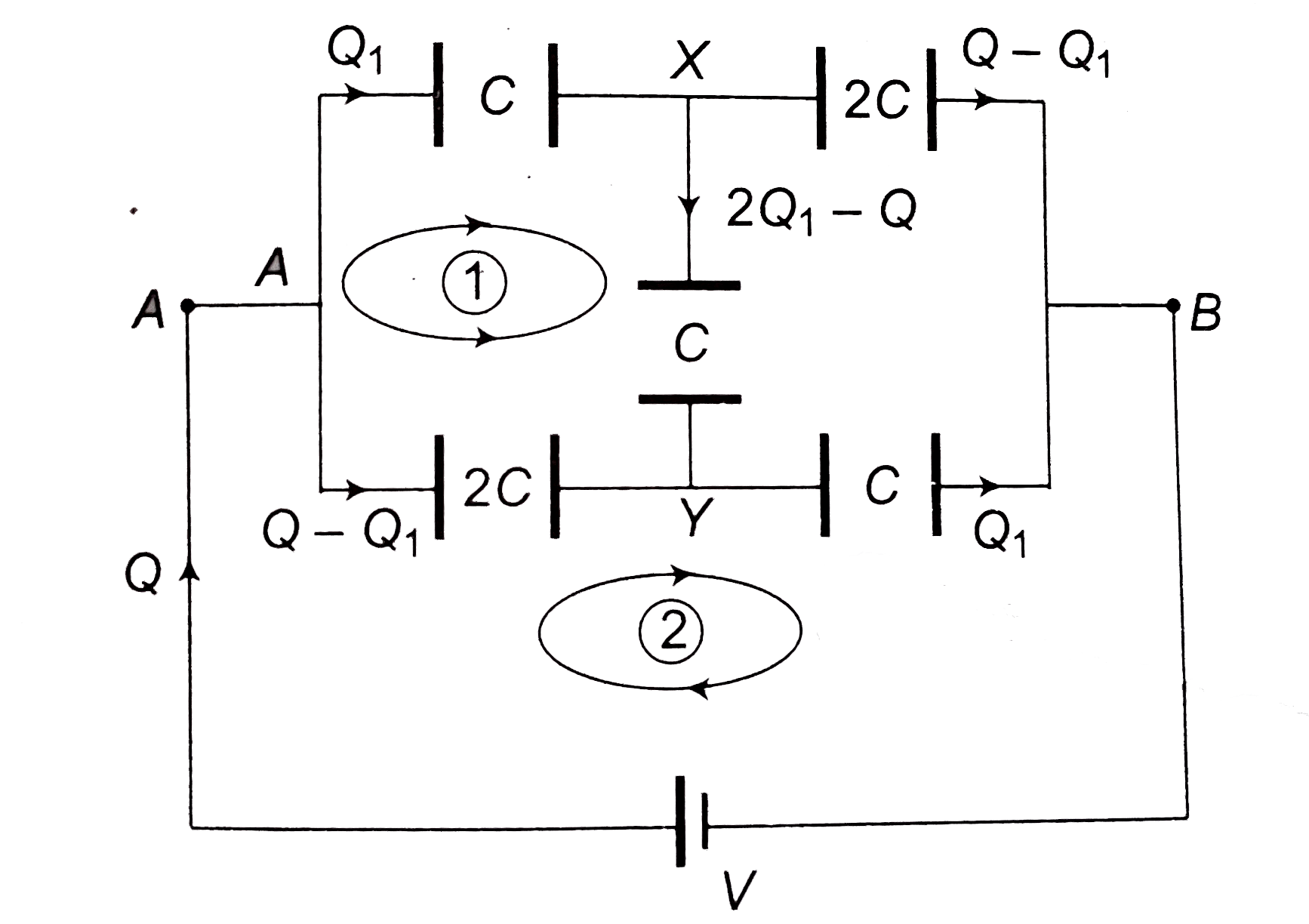 `Lo op ①, A to A , path AXYA` `V_A -(Q_1)/(C) -(2 Q_1 -Q)/(C) +(Q -Q_1)/(2C) = V_A` `-2 Q_1 - 4 Q_1 + 2Q + Q - Q_1 = 0` `7 Q_1 = 3 Q rArr Q_1 = 3 Q//7` `Lo op ②, A to A, path AYBA` `V_A -(Q -Q_1)/(2C) -(Q_1)/(C)+ V = V_A` `(Q -Q_1)/(2 C) + (Q_1)/(C) = V` `(Q_ + Q_1)/(2 C) = (Q + 3 Q//7)/(2 C) = V` `(10 Q)/(14 C) = V rArr (Q)/(V) = (14 C)/(10) = (7C)/(5)` `C_(eq) = (7 C)/(5)` Alternately by Delta-start method :  Replace Delta `APQ` by a star `X = C + 2C + (C . 2C)/(C) = 5 C` `y = C + C + (C.C)/(2 C) = (5 C)/(2)` `z = C + 2C + (C.2C)/(C) = 5 C` 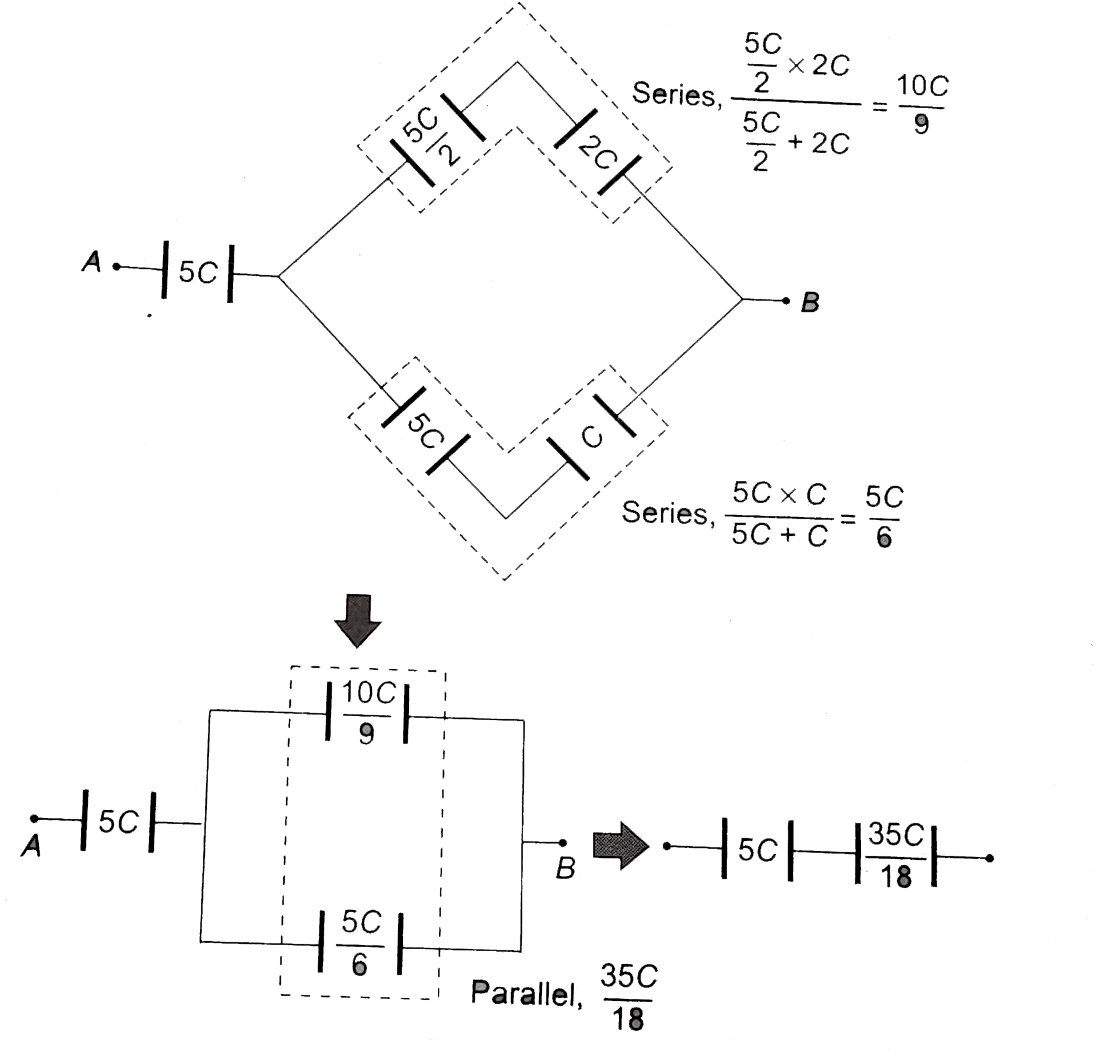 `C_(eq) = (5 C xx (35 C)/(18) )/(5C + (35)/(18)) = (7 C)/(5)` (b)  By symmetry, branches `AXB` and `PXQ` are not CONNECTED. MAKE branch `AXB` as shown. 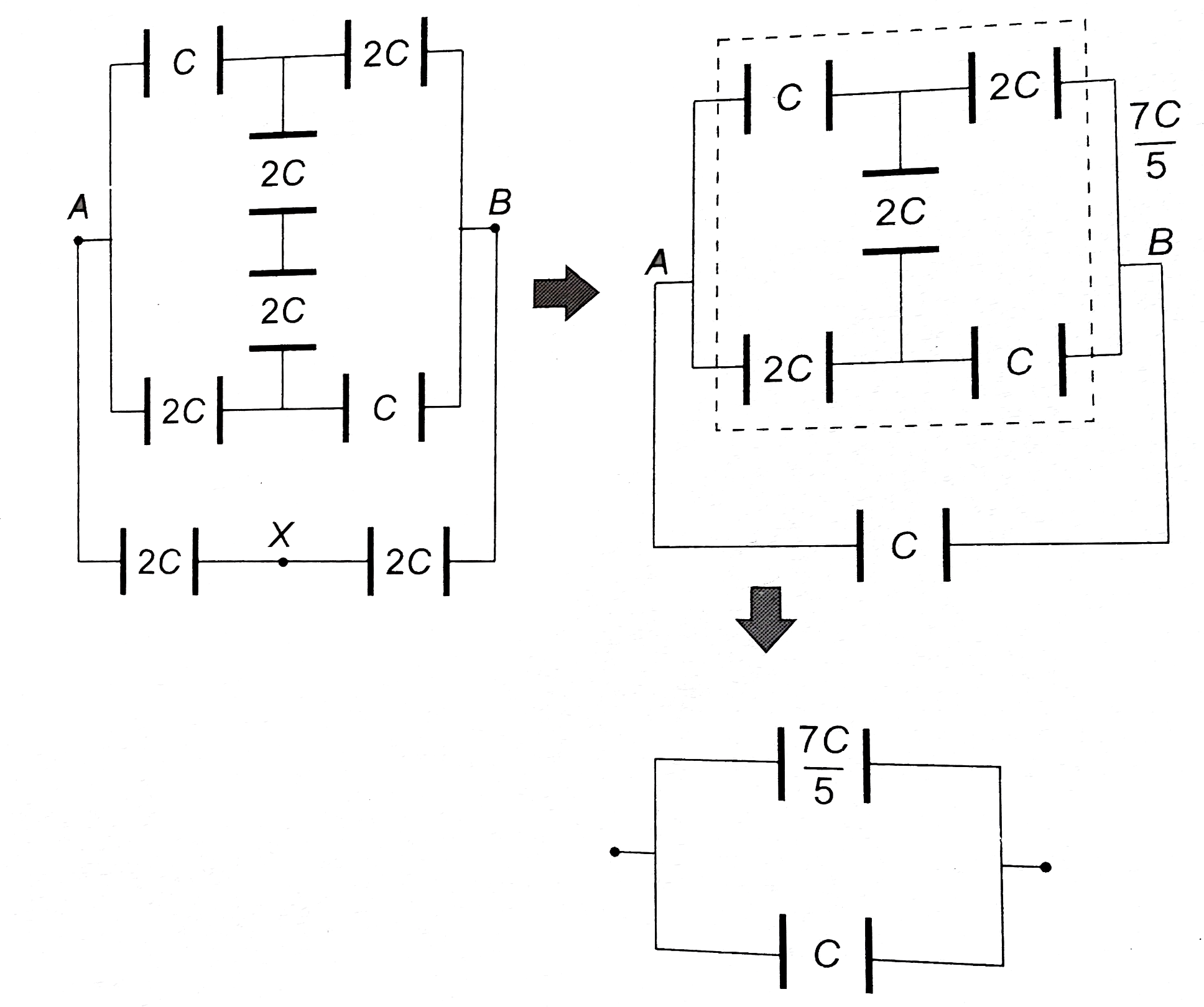 `C_(eq) = (7 C)/(5) + C = (12 C)/(5)`. |
|