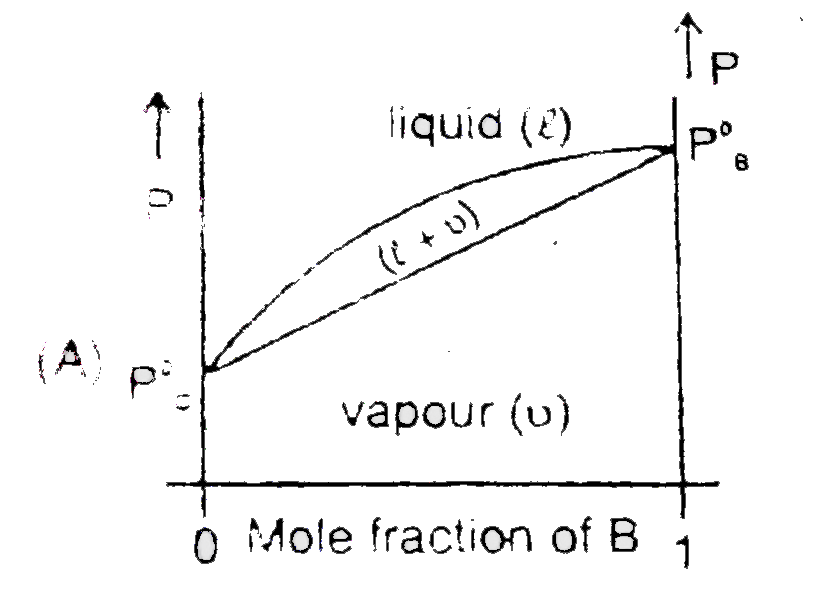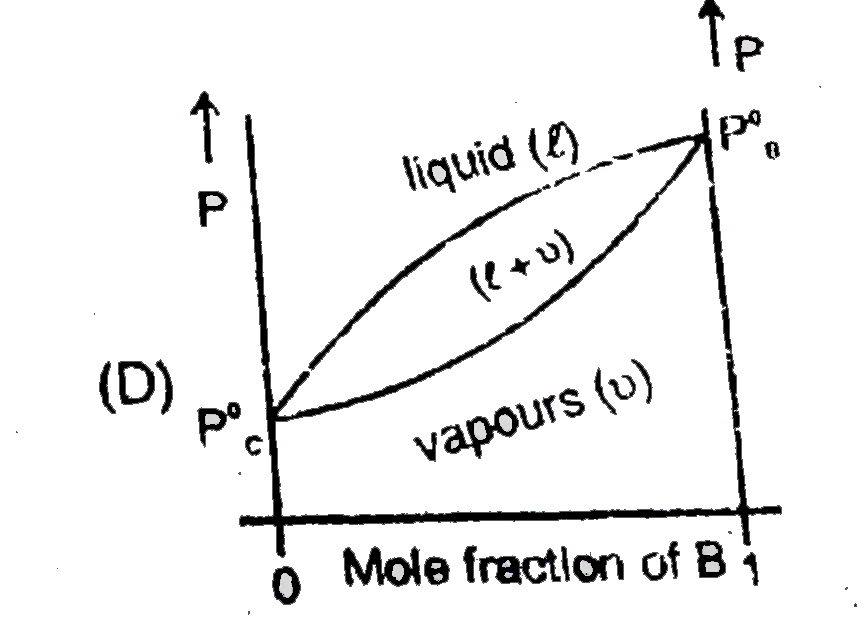Ideal Solution at Fixed Temperature Consider two liquids 'B' and 'C' that form an ideal solution We hold the temperature fixed at some value T that is above the freezing point of 'B' and 'C' We shall plo the system's pressure P against x_B,The overall mole fraction of B in the system : x_B=(n_(B_"total"))/(n_"total")=(n_B^l+n_B^v)/(n_B^v+n_C^l+n_C^v+n_B^l) Where n_B^l and n_B^v are the number of moles of B in the liquid and vapor phases, respectively, For a closed system x_B is fixed, although n_B^l and n_B^v may very. Let the system be enclosed in a cylinder fitted with a piston and immersed in a constant temperature bath To see what the P-versus - x_B phase diagram looks like let us initially set the external pressure on the piston high enough for the system to be entirely liquid (point A in figure ) As the pressure is lowered below that at A.the system eventually reaches a pressure where the liquid just begins to vaporizes (point D).At point D, the liquid has composition x_B^l where x_B^l at D is equal to the overall mole fraction x_B since only an infinitesimal amount of liquid has vapourized.What is the composition of the first vapour that comes off ? Raoult's law, P_B=x_B^vP_B^0 relates the vapour-phase mole fractions to the liquid composition as follows : x_B^v=(x_B^lP_B^0)/P and x_C^v=(x_C^lP_C^0)/P...(1) Where P_B^0 and P_C^0 are the vapour pressure of pure 'B' and pure 'C' at T where the system's pressure P equals the sum P_B+P_C of the parial pressures, where x_B^l=(n_B^l)/((n_B^l+n_C^l)) , and the vapour is assumed ideal. x_B^v/x_C^v=(x_B^lP_B^.)/(x_C^lP_C^.) ideal solution ...(2) Let B be the more volatile component meaning that P_B^0 gtP_C^0 Above equaion then show that x_B^v//x_C^v gt x_B^l//x_C^l .The vapour above an ideal solution is richer than the liquid in the more volatile component.Equations (1) and (2) apply at any pressure where liquid vapour equilibrium exists, not just at point D. Now let us isothermally lower the pressure below pointD,causing more liquid to vaporize . Eventually , we reach point F in figure. where the last drop of liquid vaporizes.Below F, we have only vapour . For any point on the line between D and F liquid and vapour phases coexist in equilibrium . If the above process is repeated for all other composition of mixture of C and B If all the points where vapours start converting into liquid are connectted and all the points where vapours get completely converted into liquid are connected then obtained graph will look like :