Saved Bookmarks
| 1. |
If the radius of an octahedral void is r and the radius of atom is close packing is R, derive the relationship between r and R. |
|
Answer» Solution :The RADIUS of the sphere representing an octahedral void can be CALCULATED by considering the cross-section through void. The cross-section of the octahedron is a square and it is shown in FIG. Let the radius of octahedral void is r and the radius of sphere is R. In the isosceles TRIANGLE ABC, `(AC)/(AB)= (sqrt(2))/(1)` 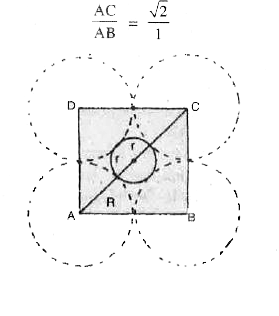 Now, AB = 2R AC = R + 2r +R `:.(2R+ 2r)/(2R)= (sqrt(2))/(1)` or `1+ (r)/(R)= (sqrt(2))/(1)` or ` (r)/(R)= sqrt(2)-1= 0.414` orr= 0.414 R Thus, for an atom to occupy an octahedral void, its radius must be 0.414 TIMES the radius of the sphere. |
|