Saved Bookmarks
| 1. |
Is an octahedral crystal field, draw the figure to show splitting of d orbitals . |
|
Answer» Solution :Step 1 : In an isolated gaseous state, all the five d orbitals of the central metal ion are degenerate. Initially, the ligands form a spherical field ofnegative charge around the metal . In this filed, the energies of all the five d orbitals will increase due to the repulsion between the electrons of the metal and the ligand. Step 2 : The ligands are approaching the metal atom in actual bond directions. To illustrate this let us CONSIDER an octahedral field, in which the central metal ion is located at the origin and the six ligands are coming from the `+x`, `-x`, `+y`, `-y`, `+z` and `-z` directions as shown below. As shown in the figure, the orbitals lying ALONG the axes `dx^(2)-y^(2)` and `dz^(2)` orbitals will experience strong repulsion and raise in energy to a GREATER extent than the orbitals with lobes directed between the axes (`d_(xy)`, `d_(yz)` and `d_(zx)`). Thus the degenerate d orbitals now split into two sets and the process is called crystal field splitting.  Step 3 : Up to this point the complex formation would not be favoured. However,when the ligands approach further, there will be an attraction between the negatively charged electron and the positively charfed metal ion, that results in a net decrease in energy. This decrease in energy in the driving FORCE for the complex formation. During crystal field splitting in octahedral field, in order to maintain the average energy of the orbitals (barycentre) constant, the energy of the orbitals `d_(x^(2)-y^(2))` and `d_(z^(2))` (represented as `e_(g)` orbitals) will increase by `3//5Delta_(0)` while that of the other three orbitals `d_(xy)`, `d_(yz)` and `d_(zx)` (represented as `t_(2g)` orbitals) decrease by `2//5Delta_(0)`. Here , `Delta_(0)` represents the crystal field splitting energy in the octahedral field. 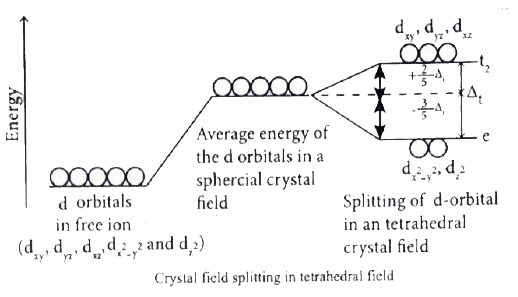
|
|
Discussion
No Comment Found
Related InterviewSolutions
- Which of the following compounds is not cleaved by HI even at 525 K ?
- To a 25 mL H_(2)O_(2) solution excess of an acidified solution of potassium iodide was added. The iodine liberated required 20 " mL of " 0.3 N sodium thiosulphate solution Calculate the volume strength of H_(2)O_(2) solution.
- The suggested mechanism of a reaction is : (a) A+BhArrD("fast) "(b)A+Drarr2C("slow")Write the balanced equation of the reaction if its experimentally deduced rate equation is , rate k=[A]^(2)[B] Find the intermediate formed during the course of the reaction . Does the predicted rate law from the mechanism match the experimental rate law ?
- Which of these changes with time for a first-order reaction A Rate of reaction B . Rate constant C . Half-life
- What is the hybridisation of central atom in the product obtained along with hydrofluoric acid when complete hydrolysis of Xenon Hexa Fluoride takes place ?
- Which of the following amino acid forms sulphide bond in polypeptide
- Which of following pair is Diastereomers:
- What is the major product of the following reaction CH_3C-=C-CH_2-CH_3overset("1 mole of " Cl_2)to
- Which polymer is used in petrol tank linings ?
- Which of the following carbohydrates are branched polymer of glucose ?