Saved Bookmarks
| 1. |
Match column-I to column-II standard entropy in KJ/k-molar at 25^(@)C {:("Column-I","Column-II"),(1.DeltaH_(C-C),(p)733.48),(2.DeltaH_(C-H),(q)97.81),(3.DeltaH_(C=C),(r)434.3),(4.DeltaH_(C-=C),(s)454.64),(5.DeltaH_(C=O),(f)804.22):} Using the dat (all values are in KJ/mol at 25^(@)C) given below: {:(DeltaH_("combustion")^(@)("ethane")=-1559.8 "",""DeltaH_("combustion")("ethane")=-1410.9),(DeltaH_("combustion")^(@)("acetylene")=-1299.7 "",""DeltaH_("combustion")("acetaldehyde")=-1192.3),(DeltaH_(f)^(@)CO_(2)(g)=-393.5 "",""DeltaH_(f)^(@) "of" H_(2)O(l)=-285.8),(DeltaH^(@) "for" C_(s) ("graphite") rarr C_(g)=716.68 "","""Bond energy of H-H =435.94"),("Bond energy of O=O=498.94 "","" ):} |
|
Answer» `{:(,1,2,3,4,5),((A),q,s,r,p,t):}` `15559.8 = 2 xx (-285.8)+ 3 xx (-285.8)-DeltaH_(f(C_(2)H_(6))` `implies "" DeltaH_(f(C_(2)H_(6)) =- 84.6.`  `DeltaH' =0-6 xx BE_(C-H)-BE_(C-C)` `2XX 716.68 + 3 xx 435.94 - 6BE_(C-H) - BE_(C-C) =- 84.6.` `6BE_(C-H)+BE_(C-C) = 2741.18 KJ. ""......(i)` `Ch_(2)CHO + (5)/(2)O_(2) rarr 2CO_(2) + 2H_(2)O, 1192.3.` `-1192.3 = 2xx (-393.5)+ 2 xx (-285.8)-1192.3` 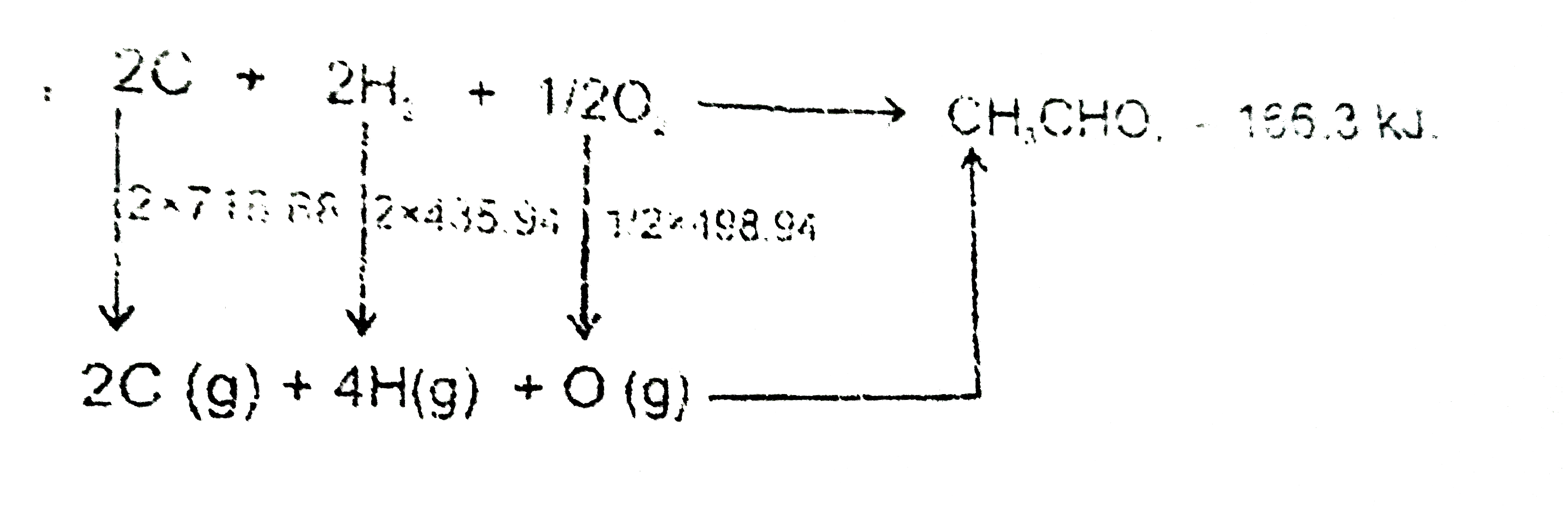 `DeltaH_(f(CH_(3)CHO)) =- 116.3 KJ.` `DeltaH'=0-4 xx BE_(C-H)-BE_(C=0)` `-166.3 =2xx 716.68 + 2 xx 435.94 +(1)/(2) xx 498.94 - 4BE_(C-H) - BE_(C=0) "".....(ii)`  `DeltaH' = 0-2 xx BE_(C=0)` `716.68 + 498.94 -2 xx BE_(C=0)=- 393.5` `BE_(C=0)=804.56 KJ. "".....(iii) ` Now we can find all bond energies. |
|