3694 + Interview Questions in Maths in Class 10 Page 13 InterviewSolution

601.	(i) Two circles with different radii are similar. (ii) Any two rectangels are similar. (iii) If two triangles are similar then their coresponding angles are equaland their corresponding sides are equal. (iv) The lenghts of the line segment joining the midpoints of any two sides of a triangle is equal to half lenge of the third side. (v) In a Delta ABC, AB=6 cm, angle A= 45^(@) and AC=8 cmand "in" a Delta DEF, DF=9 cm , angle D=45^(@) and DE=12 cm "then" Delta ABC~ Delta DEF. (vi) The polygon formed by joining the midpointsof the sies of a quadrilaterla is a rhombus. (vii) The ratio of the areas of two similar triangls is equal to the ratio of thier corresponding angle-bisector segments. (viii) The ratio of the perimeeters of twosimilar triangles is the same as the ratio of their corresponding medians. (ix) If O is any point inside a rectangle ABCDthen OA^(2)+OC^(2)=OB^(2)+OD^(2) (x)The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals.
Answer» Solution :(ii) Two rectanglesare similar only if their corresponding sides ar proportiona. (ii) if two TRIANGLES are similar, then (a) their corresponding angels are equal (B) their corresponding sides are proportional (but not necessarily equal) (iv)Let D and E be the midpoints of sides AB and AC respectively of a `Delta ABC`. Then, by the midpoint theorem, `DE\|\|BC rArr Delta ADE~Delta ABC`. `:. (AD)/(AB)=(DE)/(BC) rArr (1)/(2) (DE)/(BC)rArr DE=(1)/(2) BC`. (v) We have `(AB)/(DE)=(6)/(12)=(1)/(2), (AC)/(DE)=(8)/(9)` ltbrClearly, `(AB)/(DE)ne (AC)/(DF) and so Delta ABC` is no similar to `Delta DEF`. Note Here `Delta ABC~Delta DEF`. (vi) The polygon formed by joining the midpoints of th sides of a quadrilaterla is a parallelogram (not necessarily a rhombus) (vii) The ratio of the perimeters of two similar triangles is the same of the ratio of their corresponding sides which is the same as the ratio of the corresponding medians.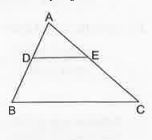

Discussion

602.	If the point (x,y) is equidistant from (7,1) and (3,5) , then
Answer» x+y=2 x-y=2 y=x+2 x+y=-2 Answer :B

Discussion

603.	A rational number lying between sqrt(2) and sqrt(3) is
Answer» `((sqrt(2) + sqrt(3))/(2))` `sqrt(6)` `1.6` `1.9` ANSWER :C

Discussion

604.	If 5 tan theta -4 = 0, then the value of (5 sin theta - 4 cos theta )/( 5 sin theta + 4 cos theta ) is
Answer» `(5)/(3)` `( 5)/(6)` 0 `(1)/(6)` ANSWER :C

Discussion

605.	In trianglePQR, angleP=72^(@), M is the mid point of side QR, and L and N are the feet of perpendicular drawn from M to PQ and PR respectively . If LM=MN, then what is the measure of angleNMR ?
Answer» ANSWER :`36^(@)`

Discussion

606.	How much should a man invest in 12%, Rs. 150 shares of a company available at a premium of Rs. 30, if the annual income earned is to be Rs. 3,600 ?
Answer» ANSWER :RS. 36,000

Discussion

607.	A chemist has two solutions of hydrochloric acid in stock. One is 50% solution and the other is 80% solution. How much of each should be used to obtain 100 ml of a 68% solution?
Answer» ANSWER :40 ML and 60 ml

Discussion

608.	For the following A.P.s, write the first term and the common difference. i] 3, 1, -1, -3, … ii] -5, -1, 3, 7, … iii] (1)/(3) , (5)/(3), (9)/(3) , (13)/(3) , …. iv] 0.6, 1.7, 2.8, 3.9, ..
Answer» ANSWER :(i)=3 (II)=4 (III)0-6

Discussion

609.	Harpreet tosses two different coins simultaneously (say one is of Rs 1 and the other of Rs 2). What is the probability that she gets atleast one head ?
Answer» ANSWER :`3/4`

Discussion

610.	State which of the following sets are empty and which are not? The set of lines passing through a given point.
Answer» ANSWER :(i) Not emtpy (II) Empty (III)Empty (IV)Empty (v) Not emtpy

Discussion

611.	find equation of circle concentric with circle 4x^2+4y^2-12x-16y-21=0and of half its area.
Answer» ANSWER :`2X^(2)+2Y^(2)-6x+8y+1+0`

Discussion

612.	Prove that : sqrt((1+cosA)/(1-cosA))+sqrt((1-cosA)/(1+cosA))=2" cosec"A
Answer» ANSWER :`

Discussion

613.	Write the following sets in roster-form. A={x:x is a natural number greater than 50 but smaller than 100}
Answer» ANSWER :(i) A={51,52,53.....,98,99} (ii) B={+2,-2} (III) D={L,O,Y,A}

Discussion

614.	In the following question, arrange the given words in meaningful sequence and then choose the most appropriate sequence from amongst the alternatives provided below :(a)Protect (b)Pressure (c )Relied (d)Rain (e )Flood
Answer» (B),(d),(C ),(a),(E ) (b),(d),(e ),(a),(c ) (b),(e ),(d),(a),(c ) (c ),(b),(d),(e ),(a)

Discussion

615.	Use the Remainder Theorem to find which of the following is a factor of 2x^3 + 3x^2- 5x - 6. (i) x+1 (ii) 2x-1 (iii) x+2
Answer» ANSWER :(i) x+1 and (III) x+2

Discussion

616.	Write the formula to find the length of DCT.
Answer» ANSWER :`SQRT(d^(2)-(R-r)^(2))`

Discussion

617.	A manufacturer makes two models A and B of a product. Each model is processed by two machines. To complete one unit of model. A, machines I and II must work1 hours and 3 hours respectively. To complete one unit of model B, machine I and II must work 2 hours and 1 hour respectively. Machine I may not operate for more than 8 hours per day, and machine II for not more than 9 hours per day. If profits on model A and B per unit are Rs. 300 and Rs. 350, then how many units of each model should be produced , per day, to maximize the profits ?
Answer» Solution :Let the MANUFACTURER produce x unit of model A and y of model B `implies x ge 0,y ge 0`. ltbr/gt `:.` Profit FUNCTION `d=300x+350 y`. To make x and y UNITS of model A and B, machine I should be used only 8 hours per day. `:. X+ 2y le 8` and machine II should be used for at the most 9 hours per day . `3x +y le 9 and x ge 0, y ge 0` Hence, we maximize f=300x+350y, subject to the constraints. `x+ 2y le 8` `3x+y le 9` `x ge 0, y ge 0` As `x ge 0 and y gt 0`, the FEASIBLE region lies in the first quadrant. The graph of `x+2y le 8` is shown with horizontal lines and the graph of `3x +y le 9` is shown with vertical lines. `:.` The feasible region is the part of the first quadrant in which there are both horizontal and verical line. The shaded region is the closed polygon having vertices O90,0) ,A (3,0), B(2,3) and C(0,4). Profit function f=300x+350 y At vertex O(0,0),f=300(0)+350(0)=0 At vertex A(3,0), f=300(3)+350(0)=900 At vertex B(2,3),f=300(2)+350(3)=600+1050=1650 At vertex C(0,4) , f=300(0)+350(4)=1400 `:.` f is maximum at the vertex B(2,3). Hence, in order to get the maximum profit, the manufacturer has to produce 2 units of model A and 3 units of model B per day .

Discussion

618.	Write some more mathematical models which you have learnt in previous classes.
Answer» <P> ANSWER :`= 4 xx "side" (or) P = 4s`

Discussion

619.	Prove that the point (x, sqrt(1-x^(2))) is at a distance of 1 unit from the origin .
Answer» Answer :PROVE by using AREA of triangle=0 if points are COLLINEAR.

Discussion

620.	A passenger, while boarding the plane, slipped from the stairsand gothurt. The pilot took the passenger in the emergencyclinic at the airport for treatment. Due to this, the plane got delayed by half an hour. To reach the destination 1500 km away in time , so that the passengers could catch the connectingflight , the speedof the plane was increased by 250 km/h thanthe usualspeed. Find the usualspeed of the plane.Whatvalue is depicted in thisquestion ?
Answer» ANSWER :750 km/h

Discussion

621.	Half the perimeter of a rectanguler garden id 36m. If the length is 4m more than its width. Find the dimensions of the garden.
Answer» ANSWER :LENGTH = 20 m; eidth = 16 m

Discussion

622.	Find the discriminant of the quadratic equation 2x^(2)-4x+3=0, and hence find the nature of its roots.
Answer» ANSWER :no REAL ROOTS

Discussion

623.	Solve for x and y, px + qy = 1 andqx + py = ((p - q)^(2))/(p^(2) + q^(2))-1.
Answer» <P> ANSWER :`X = (p)/(p^(2) + Q^(2)), y = (q)/(p^(2) + q^(2))`

Discussion

624.	When divided by x- 3 the polynomials x^3-px^2+x+6 and 2x^3-x^2-(p+3)x-6 leave the same remainder. Find the value of 'p'.
Answer» ANSWER :p=1

Discussion

625.	Find the 20th and nth term of the GP. 5/2, 5/4, 5/8………
Answer» ANSWER :`a_(20) = 5/2^(20)` (II) `a_(n) = 5/(2^(n))`

Discussion

626.	Two water taps together can fill a tank is 9 3/8 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.
Answer» ANSWER :15 HRS

Discussion

627.	Check whether the following equations are consistent or inconsistent. Solve them graphically. (b) 2x - 3y = 8 4x - 6y = 9
Answer» ANSWER :INCONSISTENT

Discussion

628.	If A=[{:(,1,3),(,2,4):}], B=[{:(,1,2),(,4,3):}] and C=[{:(,4,3),(,1,2):}]. Find (i) (AB) C (ii) A (BC) Is A(BC)=(AB) C?
Answer» ANSWER :(i) `[{:(,63,61),(,88,86):}]` (II) `[{:(,63,61),(,88,86):}]` YES

Discussion

629.	If \|A\| = 5, \|B_(1)\| = 5 " and " \|B_(2)\| = 25, then find the values of x and y in Cramer's method.
Answer» ANSWER :X, y = 3, 5 RESPECTIVELY

Discussion

630.	Factorise the expression f(x)=2x^(3)-7x^(2)-3x+18, Hence, find all possible values of x for which f(x)=0.
Answer» ANSWER :`(x-2) (x-3) (2x+3); 2,3,-3/2`

Discussion

631.	King: Crown :: ?
Answer» SCULPTOR : Chisel Teacher : Chalk Soldier : Gun Priest : Mitre Solution :FIRST is DIGNIFIED by the SECOND

Discussion

632.	Ashok invested 26400rs in 12% , 25rs shares of a company. If he receives a dividend of 2475rs find the (i) number of shares he bought (ii) market value of each share.
Answer» ANSWER :`(i)825` `(II) 32rs`

Discussion

633.	Find the 10th term from the end of the A.P. 4, 9, 14,…………. 254.
Answer» ANSWER :209

Discussion

634.	In the figure ,XP,XQ and XR are tangents to the circles.If the length of XQ =9 cm ,then the length of tangent XR is :
Answer» 18 cm 10 cm 9 cm 12 cm Answer :C

Discussion

635.	Find the remainder when 3^(215) is divided by 43.
Answer» 35 28 33 30 Answer :B

Discussion

636.	Find the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.
Answer» ANSWER :42 `CM^(2)`

Discussion

637.	Solve the following equation : 2((2x-1)/(x+3))-3((x+3)/(2x-1))=5,(xne-3,1)
Answer» SOLUTION :Given equation is `2((2x-1)/(x+3))-3((x+3)/(2x-1))=5"".....(i)` LET `(2x-1)/(x+3)=y.....(II)` HENCE, `(x+3)/(2x-1)=(1)/(y)` Now from equation (1) `2y-(3)/(y)=5` `implies2y^(2)-3=5y` `implies2y^(2)-5y-3=0` `implies2y^(2)-(6-1)y-3=0` `implies2y^(2)-6y+1y-3=0` `implies2y(y-3)+1(y-3)=0` `implies(2y+1)(y-3)=0` `implies2y+1=0ory-3=0` when `implies2y+1=0impliesy=-(1)/(2)` and `y-3=0impliesy=3` SUBSTITUTING values of y in equation (2) when `y=-(1)/(2)` `(2x-1)/(x+3)=-(1)/(2)` `implies2(2x-1)=-1(x+3)implies4x-2=-x-3` `implies5x=-1impliesx=-(1)/(5)` when y=3 `(2x-1)/(x+3)=3` `implies2x-1=3(x+3)implies2x-1=3x+9` `implies-x=10impliesx=-10` Hence, `x=-10orx=-(1)/(5)` are roots of the equation.

Discussion

638.	Determine whether the following points are collinear L(2, 5), M(3, 3), N(5, 1)
Answer» ANSWER :No

Discussion

639.	Find the median for the following data :
Answer» ANSWER :35

Discussion

640.	Show that the line segment S joining the points (-6, 8) (-2, 4) and (-4, 13), (-4,-1) bisects each other
Answer» ANSWER :line segment JOINING the points `(-6, 8) (-2, 4) and (-4, 13), (-4, -1)` bisects each other

Discussion

641.	In the following A.P.'s, find the missing terms in the boxes.
Answer» <P> Solution :(i) `2, square , 26` `RARR 2,x,26` are in A.P. (say) `rArr x=(2+26)/(2)=14` (ii)`square, 13,square,3` `rArr x,13,y,3` are in A.P. (say) `:. Y=(13+3)/(2)=8` and `(x+y)/(2)=13` `rArrx+y=26` `rArr x+8=26` `rArr x=18` `rArr x=18,y=8` (ii) `5,square,square,9(1)/(2)` `rArr 5,x,y,(19)/(2)` are in A.P.. (say) Here, a=5 and `a_(4)=(19)/(2)` `rArr 5+3D=(19)/(2)` `rArr 3d=(19)/(2)-5=(9)/(2) rArr d=(3)/(2)` `:. x=5+d=5+(3)/(2)=(13)/(2)` and `y=5+2d=5+2xx(3)/(2)=8` `:. x=(13)/(2),y=8` (iv) `-4square,square,square,square,6` `rArr -4,p,q,r,s,6` are in A.P. (say) Here, `a=-4` and `a_(6)=6` `rArr -4+5d=6` `rArr 5d=10 rArrd=2` `:. p=-4+d=-4+2=-2` `q=-4+2d=-4+2xx2=0` `r=-4+3d=-4+3xx2=2` `s=-4+4d=-4+4xx2=4` `p=-2,q=0,r=2,s=4` (v)`square,38,square,square,square,-22` `rArr p, 38,q,r,s,-22 ` are in A.P. (say) Here, `a_(2)=38` `rArr p+d=38 "" ...(1)` and `a_(6)=-22` `rArr p+5d=-22 "" ...(2) ` Subtract equation (1) from (2), we get `{:(p+5d=""-22),(underset(-)" "punderset(-)+d=""underset(-)38),(bar(""4d=-60" ")):}` `rArr"" d=-15` put d=-15 in equation (1), we get p+(-15)=38 `rArr p=53` `:. q=38+d=38+(-15)=23` `r=q+d=23+(-15)=8` `s=r+d=8+(-15)=-7` `:. p=53, q=23, r=8, s=-7`

Discussion

642.	If B=2, H=8 and CAB=6, then what is the number value of RACE?
Answer» 31 30 28 27 Solution :CLEARLY in a given CODE: A= 1, B=2, C=3 etc. Now C A B `=3 + 1 + 2=6` `:.` RACE `=18 + 1 + 3 +5`= 27

Discussion

643.	For what values of ‘k’, k - 3, 26 + 1 and 4k + 3 are in AP?
Answer» ANSWER :k=2

Discussion

644.	Collect the details and find the probabilites of selecting a girl from tenth standard in your school.
Answer»

Discussion

645.	If A and B are any two 2 xx 2 matrices such that AB=BA=B and B is not a zero matrix, what can you say about the matrix A ?
Answer» ANSWER :A is the IDENTITY MATRIX

Discussion

646.	If A=[{:(,2),(,5):}], B=[{:(,1),(,4):}] and C=[{:(,6),(,-2):}], find (i) B+C (ii) A-C (iii) A+B-C (iv) A-B+C
Answer» ANSWER :(i) `[{:(,7),(,2):}]` (ii) `[{:(,-4),(,7):}]` (iii) `[{:(,-3),(,11):}]` (IV) `[{:(,7),(,-1):}]`

Discussion

647.	10th term of the A.P. 2,7,12,…….is
Answer» `-47` `47` `57` NONE of these ANSWER :D

Discussion

648.	Prove that the tangents drawn at the ends of a diameter of a circle are parallel.
Answer»

Discussion

649.	The point P(5,1) and Q(-2,-2) are reflected in line x = 2 . Use graph paper to find the images P' and Q' of points P and Q respectively in line x = 2 . Take 2 cm equal to 2 units.
Answer» <P> ANSWER :P' = (-1,1) , Q' (6,-2)

Discussion

650.	A vessel, in the form of an inverted cone, is filled with water to the brim. Its height is 20 cm and diameter is 16.8 cm. Two equal solid cones are dropped in it so that they are fully submerged. As a result, one-third of the water in the original cone overflows. What is the volume of each of the solid cones submerged ?
Answer» ANSWER :`246.4 CM ^(2)`

Discussion

Explore topic-wise InterviewSolutions in .

If the point (x,y) is equidistant from (7,1) and (3,5) , then

A rational number lying between sqrt(2) and sqrt(3) is

If 5 tan theta -4 = 0, then the value of (5 sin theta - 4 cos theta )/( 5 sin theta + 4 cos theta ) is

In trianglePQR, angleP=72^(@), M is the mid point of side QR, and L and N are the feet of perpendicular drawn from M to PQ and PR respectively . If LM=MN, then what is the measure of angleNMR ?

How much should a man invest in 12%, Rs. 150 shares of a company available at a premium of Rs. 30, if the annual income earned is to be Rs. 3,600 ?

A chemist has two solutions of hydrochloric acid in stock. One is 50% solution and the other is 80% solution. How much of each should be used to obtain 100 ml of a 68% solution?

For the following A.P.s, write the first term and the common difference. i] 3, 1, -1, -3, … ii] -5, -1, 3, 7, … iii] (1)/(3) , (5)/(3), (9)/(3) , (13)/(3) , …. iv] 0.6, 1.7, 2.8, 3.9, ..

Harpreet tosses two different coins simultaneously (say one is of Rs 1 and the other of Rs 2). What is the probability that she gets atleast one head ?

State which of the following sets are empty and which are not? The set of lines passing through a given point.

find equation of circle concentric with circle 4x^2+4y^2-12x-16y-21=0and of half its area.

Prove that : sqrt((1+cosA)/(1-cosA))+sqrt((1-cosA)/(1+cosA))=2" cosec"A

Write the following sets in roster-form. A={x:x is a natural number greater than 50 but smaller than 100}

In the following question, arrange the given words in meaningful sequence and then choose the most appropriate sequence from amongst the alternatives provided below :(a)Protect (b)Pressure (c )Relied (d)Rain (e )Flood

Use the Remainder Theorem to find which of the following is a factor of 2x^3 + 3x^2- 5x - 6. (i) x+1 (ii) 2x-1 (iii) x+2

Write the formula to find the length of DCT.

Write some more mathematical models which you have learnt in previous classes.

Prove that the point (x, sqrt(1-x^(2))) is at a distance of 1 unit from the origin .

Half the perimeter of a rectanguler garden id 36m. If the length is 4m more than its width. Find the dimensions of the garden.

Find the discriminant of the quadratic equation 2x^(2)-4x+3=0, and hence find the nature of its roots.

Solve for x and y, px + qy = 1 andqx + py = ((p - q)^(2))/(p^(2) + q^(2))-1.

When divided by x- 3 the polynomials x^3-px^2+x+6 and 2x^3-x^2-(p+3)x-6 leave the same remainder. Find the value of 'p'.

Find the 20th and nth term of the GP. 5/2, 5/4, 5/8………

Two water taps together can fill a tank is 9 3/8 hours. The tap of larger diameter takes 10 hours less than the smaller one to fill the tank separately. Find the time in which each tap can separately fill the tank.

Check whether the following equations are consistent or inconsistent. Solve them graphically. (b) 2x - 3y = 8 4x - 6y = 9

If A=[{:(,1,3),(,2,4):}], B=[{:(,1,2),(,4,3):}] and C=[{:(,4,3),(,1,2):}]. Find (i) (AB) C (ii) A (BC) Is A(BC)=(AB) C?

If |A| = 5, |B_(1)| = 5 " and " |B_(2)| = 25, then find the values of x and y in Cramer's method.

Factorise the expression f(x)=2x^(3)-7x^(2)-3x+18, Hence, find all possible values of x for which f(x)=0.

King: Crown :: ?

Ashok invested 26400rs in 12% , 25rs shares of a company. If he receives a dividend of 2475rs find the (i) number of shares he bought (ii) market value of each share.

Find the 10th term from the end of the A.P. 4, 9, 14,…………. 254.

In the figure ,XP,XQ and XR are tangents to the circles.If the length of XQ =9 cm ,then the length of tangent XR is :

Find the remainder when 3^(215) is divided by 43.

Find the area of the shaded region as shown in figure, where ABCD is square of side 14 cm.

Solve the following equation : 2((2x-1)/(x+3))-3((x+3)/(2x-1))=5,(xne-3,1)

Determine whether the following points are collinear L(2, 5), M(3, 3), N(5, 1)

Find the median for the following data :

Show that the line segment S joining the points (-6, 8) (-2, 4) and (-4, 13), (-4,-1) bisects each other

In the following A.P.'s, find the missing terms in the boxes.

If B=2, H=8 and CAB=6, then what is the number value of RACE?

For what values of ‘k’, k - 3, 26 + 1 and 4k + 3 are in AP?

Collect the details and find the probabilites of selecting a girl from tenth standard in your school.

If A and B are any two 2 xx 2 matrices such that AB=BA=B and B is not a zero matrix, what can you say about the matrix A ?

If A=[{:(,2),(,5):}], B=[{:(,1),(,4):}] and C=[{:(,6),(,-2):}], find (i) B+C (ii) A-C (iii) A+B-C (iv) A-B+C

10th term of the A.P. 2,7,12,…….is

Prove that the tangents drawn at the ends of a diameter of a circle are parallel.

The point P(5,1) and Q(-2,-2) are reflected in line x = 2 . Use graph paper to find the images P' and Q' of points P and Q respectively in line x = 2 . Take 2 cm equal to 2 units.