InterviewSolution
Saved Bookmarks
| 1. |
(i) Two circles with different radii are similar. (ii) Any two rectangels are similar. (iii) If two triangles are similar then their coresponding angles are equaland their corresponding sides are equal. (iv) The lenghts of the line segment joining the midpoints of any two sides of a triangle is equal to half lenge of the third side. (v) In a Delta ABC, AB=6 cm, angle A= 45^(@) and AC=8 cmand "in" a Delta DEF, DF=9 cm , angle D=45^(@) and DE=12 cm "then" Delta ABC~ Delta DEF. (vi) The polygon formed by joining the midpointsof the sies of a quadrilaterla is a rhombus. (vii) The ratio of the areas of two similar triangls is equal to the ratio of thier corresponding angle-bisector segments. (viii) The ratio of the perimeeters of twosimilar triangles is the same as the ratio of their corresponding medians. (ix) If O is any point inside a rectangle ABCDthen OA^(2)+OC^(2)=OB^(2)+OD^(2) (x)The sum of the squares on the sides of a rhombus is equal to the sum of the squares on its diagonals. |
|
Answer» (ii) if two TRIANGLES are similar, then (a) their corresponding angels are equal (B) their corresponding sides are proportional (but not necessarily equal) (iv)Let D and E be the midpoints of sides AB and AC respectively of a `Delta ABC`. Then, by the midpoint theorem, `DE||BC rArr Delta ADE~Delta ABC`. `:. (AD)/(AB)=(DE)/(BC) rArr (1)/(2) (DE)/(BC)rArr DE=(1)/(2) BC`. (v) We have `(AB)/(DE)=(6)/(12)=(1)/(2), (AC)/(DE)=(8)/(9)` ltbrClearly, `(AB)/(DE)ne (AC)/(DF) and so Delta ABC` is no similar to `Delta DEF`. Note Here `Delta ABC~Delta DEF`. (vi) The polygon formed by joining the midpoints of th sides of a quadrilaterla is a parallelogram (not necessarily a rhombus) (vii) The ratio of the perimeters of two similar triangles is the same of the ratio of their corresponding sides which is the same as the ratio of the corresponding medians. 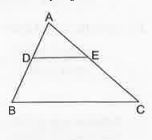
|
|