InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1251. |
A trader in order to code the prices of articles in his store, used the letters of PSICHOLAZY in the form of 0 to 9, respectively. Which of the following stands for ₹ 875.50? |
|
Answer» ZCA.OP |
|
| 1252. |
The radius of the base ofaright circular cone is 'x'. It is cut by a plane parallel to the base at a height y from the base. The distance boundary of upper surface from the base of frustum is sqrt(y^(2)+(x^(2))/(9)). Show that the volume of frustum is (13)/(27)pix^(2)ycu. units. |
|
Answer» |
|
| 1253. |
Without using trigonometric tables, prove that :(i) cos -81^@-sin 9^@=0(ii)tan 71^@-cot 19^@=0(iii) cosec 80^@-sec 10^@=0(iv) cosec ^2 72^@-tan^2 18^@=1(v)cos^2 75^@ +cos ^2 15^@=0(vi) tan^2 66^@-cot^2 24^@=0(vii) sin^2 48^@+sin^2 42^@=1(viii)cos^2 57^@-sin^2 33^@=0(ix)(sin 65^@+cos 25^@)(sin 65^@-cos25^@)=0 |
|
Answer» Solution :`(IV) LHS =cosec^2 72^@-TAN ^2(90^@-72^@)=cosec^2 72^@-cot ^272=1`. J `(viii) LHS-cos^2 57^@-sin^2 (90^@-57^@)=cos^2 57^@-cos^2 57^@=0`. `(ix) LHS=sin^2 65^@-cos^2 25^@=sin ^2 65^@-cos^2(90-65^@)=sin^2 65^@-sin^2 65^@=0`. |
|
| 1254. |
Solve for x and y (i) [{:(,2,5),(,5,2):}] [{:(,x),(,y):}]=[{:(,-7),(,14):}] (ii) [x+y, x-4] [{:(,-1,-2),(,2,2):}]=[-7, -11] (iii) [{:(,-2,0),(,3,1):}] [{:(,-1),(,2x):}] +3[{:(,-2),(,1):}]=2 [{:(,y),(,3):}]. |
|
Answer» |
|
| 1255. |
The vertices of a triangle are (2, 1), (5, 2) and (3, 4). Then the co-ordinates of the centroid are |
|
Answer» `10, 3` |
|
| 1256. |
State whether the given statements are true or false : (i) The sum of two rationals is always rational. (ii) The sum of two irrationals is always irrational. (iii) The product of two rationals is always rational. (iv) The product of two irrationals is always irrational. (v) The sum of a rational and an irrational is always rational. (vi) The product of a rational and an irrational is always irrational. |
|
Answer» |
|
| 1257. |
Five friends P, Q, R, S and T are standing in a row facing East. Who is standing at the extreme right end? I. Only P is between S and T. R is to immediate right of T. II. R is between T and Q. |
|
Answer» the data in statement I ALONE are SUFFICIENT to answer the question, while the data in statement II alone are not sufficient to answer the question,  Thus, Q is at the extreme right end. |
|
| 1258. |
If A={3,6,9,12,15,18,21}, B={4,8,12,16,20} C={2,4,6,8,12,14,16} and D={5,10,15,20}, find (i) A-B (ii) A-C (iii) A-D (iv) B-A (v) C-A (vi) D-A (vii) B-C (viii) B-D (ix) C-B (x) D-B |
|
Answer» (ii) A-C={3,9,15,18,12} (III) A-D={3,6,9,12,18,21} (iv) B-A={4,8,16,20} (V) C-A={2,4,8,10,16} (vi) D-A={5,10,20} B-C={20} (viii) B-D={4,8,12,16} (ix) C-B={2,6,10,14} (x) D-B={5,10,15} |
|
| 1259. |
The vertices of a Delta ABC are A (4,6), B (1, 5) and C (7,2). A line is drawn to intersect sides AB and AC at D and Erespectively, such that (AD)/(AB) = (AE)/(AC) = (1)/(4).Calculate the area of DeltaADE and compare it with area of Delta ABC |
|
Answer» |
|
| 1260. |
Two ships are sailing in the sea on either side of the lighthouse. The anglesof depression of two ships as observed from the top of the lighthouse are 60^(@) and 45^(@) respectively. If the distance between the ship is 200((sqrt(3)+1))/(sqrt(3)) metres, find the height of the lighthouse. |
|
Answer» |
|
| 1261. |
If x=2 and x=3 are roots of the equation 3x^(2)-2mx+2n=0, find the values of m and n. |
|
Answer» |
|
| 1263. |
Is it possible to construct a pair of tangents from point A lying on the circle of radius 4 cm and centre O. |
|
Answer» |
|
| 1264. |
Divide c into two parts such that a times the larger part shall be equal to b times the smaller part. |
|
Answer» |
|
| 1265. |
A ready-made garment shopkeeper gives 5% discount on the dress of 1000 and charges 5% GST on the remaining amount, then what is the purchase prices of the dress for the customers? |
|
Answer» |
|
| 1266. |
Find a G.P. for which the sum of first two terms is -4 and the fifth is 4 times the third term. |
|
Answer» |
|
| 1267. |
Find the value of ‘K’ for which the points are collinear (K, K) (2, 3) and (4, -1). |
|
Answer» |
|
| 1268. |
A man bought 500 shares, each of face value 10rs of a certain business concern and during the first year after purchase, receives 400rs as dividend on his shares. Find the rate of dividend on the shares. |
|
Answer» |
|
| 1269. |
The mean of the cubes of the first n natural numbers is |
|
Answer» `(N(n + 1)^2)/2` |
|
| 1270. |
Find the seventh term of the G.P. : sqrt(3)+1,1,(sqrt(3)-1)/(2), . . . . .. . . . . |
|
Answer» |
|
| 1271. |
Construct two circles of radii 2.5 cm each, the distance of whose centres is 8 cm. Then construct a transverse common tangent to these two circles. |
Answer» Solution : Here CD is the REQUIRED tansverse common TANGENT to the circles with centres O and O'. |
|
| 1272. |
A cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter the hemisphere can have? Find the surface area of the solid. |
|
Answer» |
|
| 1273. |
If alpha and beta are zeroes of a quadratic polynomial ax^(2)+bx+c. Find the value of: (i) alpha^(2)-beta^(2) (ii) alpha^(3)+beta^(3) (iii) alpha^(4)beta+beta^(4)alpha (iv) sqrt((alpha)/(beta))+sqrt((beta)/(alpha)) (v) (alpha^(2))/(beta)+(beta^(2))/(alpha) (alpha^(-1)+(1)/(alpha^(-1)))(beta^(-1)+(1)/(beta^(-1))) |
|
Answer» (vi) `(a^(2)+b^(2)+c^(2)-2ac)/(ac)` |
|
| 1274. |
Find the number of triangles in the following figure. |
|
Answer» 9 |
|
| 1275. |
Find the mode of the given data4,5,5,4,7,2,3,4,2,4,5 |
| Answer» | |
| 1276. |
If the distances of p (x, y) from A (-1, 5) and B (5, 1) are equal, then |
|
Answer» `2x=y` |
|
| 1277. |
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2:3. Find the ratio between their curved surface areas. |
|
Answer» |
|
| 1278. |
Two right circular solid cylinders have radii in the ratio 3 : 5 and heights in the ratio 2:3. Find the ratio between their volumes. |
|
Answer» |
|
| 1279. |
Two spheres of same metal weight 1 kg and 7 kg .The radius of the smaller sphere is 3cm .The two spheres are melted to form a single big sphere.Find the diameter of the new sphere. |
|
Answer» |
|
| 1280. |
Refer to 0.5 above. Draw the less then type ogive for this data and use it to find the median weight. |
|
Answer» Solution :For less than type table we follow the Q.5 Here, we OBSERVE that, the weight of all 70 packets is more than or EQUAL to 200. Since, 13 packets lie in the interval 200-201. So, the weight of 70-12=57packets is more than or equal to 201. Continuing INT this manner we get remianing more than or equal to 202,203,204,205 and 205  To draw the less than type ogive, we PLOT the points (200,0),(201,13),(202,40),(203,40),(203,58),(204,68),(205,69),(206,70) on the paper and JOIN by free hand. To draw the more than type ogive plot the points (200,70),(201,57),(202,12) 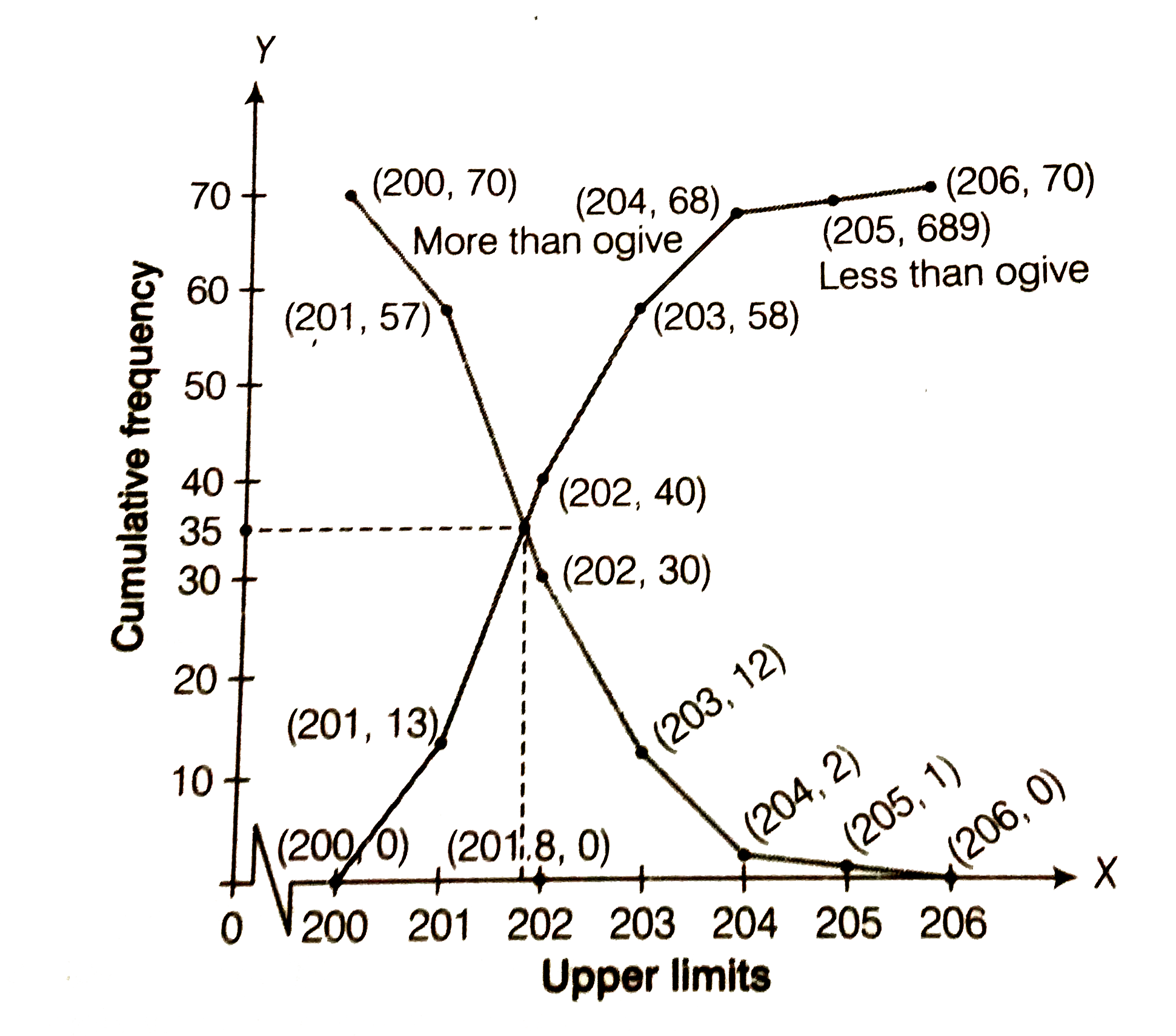 Hence, required median weight=intersection points X-axis=201.8g |
|
| 1281. |
If TP and TQ are the two tangents to a circle with centre O. So that /_PQR = 105^@, then /_PTQ is ………….. . |
|
Answer» |
|
| 1282. |
Show that (2 + sqrt(3)) is an irrational number. |
|
Answer» Solution :Let, if possible `(2 + sqrt(3))` is RATIONAL then, `2 + sqrt(3) = (a)/(b)` (say) where, a and b are integers and `b ne 0`. `rArr` `sqrt(3) = (a)/(b) - (2) ""rArr"" sqrt(3) = (a - 2b)/(b)""`…(1) `because` a and b are integers `therefore` a - 2b is also an integer. `rArr` `(a - 2b)/(b)` is rational. Now, L.H.S. of equation (1) is the square root of a prime number. So, it is irrational and R.H.S. is rational. Which is a contradiction because a rational number and an irrational number can never be equal. So, our supposition i.e., `2 + sqrt(3)` is rational, is WRONG. Hence, `(2 + sqrt(3))` is an irrational number. `""` Hence Proved. |
|
| 1283. |
Calculate the mean by step-deviation method. |
|
Answer» |
|
| 1284. |
Andya and Nitya planted some trees in a square garden as shown in the Fig. 2, both arguing thatthey have planted them in a straight line. Find who is correct ? Justify your decision. (N stands for Nitya and A for Aadya)Are the two girlscontributing anything to the society ? Justify your answer . |
|
Answer» |
|
| 1285. |
Express each of the following numbers as a product of its prime factors. 5005 |
|
Answer» |
|
| 1286. |
Given matrix A=[{:(,5),(,-3):}] and matrix B=[{:(,-1),(,7):}] find matrix X such that : A+2X=B. |
|
Answer» |
|
| 1287. |
When the polynomial x^(3)+2x^(2)-5ax-7 is divided by (x - 1), the remainder is A and when the polynomial. x^3+ax^2-12x+16 is divided by (x + 2), the remainder is B. Find the value of 'a' if 2A + B = 0. |
|
Answer» |
|
| 1288. |
Mr. Pankaj took Health Insurance Policy for his family and paid Rs. 900 as SGST. Find the total annual premium including GST, paid by him for this policy rate of GST being 18% |
|
Answer» |
|
| 1289. |
Find the sum of first 51 terms of an A.P. whose 2nd and 3rd terms are 14 and 18 respectively. |
|
Answer» |
|
| 1290. |
One card is drawn from a well - shuffled deck of 52 cards. Find the probability of getting (i) a king of red colour (ii) a face card (iii) a red face card (iv) the jack of hearts (v) a spade (vi) the queen of diamonds |
|
Answer» (II) `3/13` (III) `3/26` (iv) `1/52` (V) `1/4` (VI) `1/52` |
|
| 1291. |
How many terms are there in the series : 4,7,10,13,……..148? |
|
Answer» |
|
| 1292. |
If the cook is called butler, butler is called manager, manager is called teacher, teacher is called clerk and clerk is called principal, who will teach in the class? |
|
Answer» Cook |
|
| 1293. |
Which term of the G.P. : -10,(5)/(sqrt(3)),-(5)/(6), . . . . . .. . . . " is "-(5)/(72) ? |
|
Answer» |
|
| 1294. |
Mr. Desai sold shares of 27,250 and purchased shares of 72,750 in a day. He paid brokerage at the rate of 0.2% on sale and purchase. 18% GST was charged on brokerage. Find his total expenditure on brokerage and tax. |
|
Answer» |
|
| 1295. |
Shri. Aditya Sanghavi invested 50,118 in shares of FV 100, when the market value is 50. Rate of brokerage is 0.2% and Rate of GST on brokerage is 18%, then How many shares were purchased for 50,118? |
|
Answer» |
|
| 1296. |
(i) Six friends P, Q, R, S, T and U are members of the club and play a different game of Football, Cricket, Tennis, Basket ball, Badminton and Volley ball.(ii) T who is taller than P and S plays Tennis. (iii) The tallest among them plays Basket ball. (iv) The shortest among them plays Volley ball. (v) Q and S neither play Volley ball nor Basket ball. (vi) R plays Volley ball. (vii) T is between Q who plays Foot ball and P in order of height Who among them is taller than R but shorter than P? ( |
|
Answer» <P>Q SINCE R plays Volley BALL, so R is the shortest. Q plays neither Volley ball nor Basket ball, so Q is not the TALLEST. Thus U is the tallest. ` therefore ` the sequence becomes `U gt Q gt T gt Pgt S gt R.` Now T plays Tennis, U, being tallest, plays Basket ball. R plays Volley ball. Q plays Foot ball. Both P and S play either Cricket or Bad minton. S is taller than R but shorter than P. |
|
| 1297. |
(i) Six friends P, Q, R, S, T and U are members of the club and play a different game of Football, Cricket, Tennis, Basket ball, Badminton and Volley ball.(ii) T who is taller than P and S plays Tennis. (iii) The tallest among them plays Basket ball. (iv) The shortest among them plays Volley ball. (v) Q and S neither play Volley ball nor Basket ball. (vi) R plays Volley ball. (vii) T is between Q who plays Foot ball and P in order of height Which of the following statements is not true? |
|
Answer» P is shorter than R Since R plays Volley ball, so R is the SHORTEST. Q plays neither Volley ball nor Basket ball, so Q is not the tallest. Thus U is the tallest. ` therefore ` the sequence becomes `U gt Q gt T gt Pgt S gt R.` Now T plays Tennis, U, being tallest, plays Basket ball. R plays Volley ball. Q plays Foot ball. Both P and S play either Cricket or Bad minton. P is taller than R. |
|
| 1298. |
(i) Six friends P, Q, R, S, T and U are members of the club and play a different game of Football, Cricket, Tennis, Basket ball, Badminton and Volley ball.(ii) T who is taller than P and S plays Tennis. (iii) The tallest among them plays Basket ball. (iv) The shortest among them plays Volley ball. (v) Q and S neither play Volley ball nor Basket ball. (vi) R plays Volley ball. (vii) T is between Q who plays Foot ball and P in order of height Who will be at the third place if they are arranged in the descending order of their height? |
|
Answer» Q Since R plays VOLLEY ball, so R is the shortest. Q plays neither Volley ball nor Basket ball, so Q is not the tallest. Thus U is the tallest. ` therefore ` the sequence becomes `U gt Q gt T gt Pgt S gt R.` Now T plays Tennis, U, being tallest, plays Basket ball. R plays Volley ball. Q plays Foot ball. Both P and S play either CRICKET or Bad minton. The DESCENDING ORDER of height is U, Q, T, P, S, R. `therefore `T is at the third place. |
|
| 1299. |
(i) Six friends P, Q, R, S, T and U are members of the club and play a different game of Football, Cricket, Tennis, Basket ball, Badminton and Volley ball.(ii) T who is taller than P and S plays Tennis. (iii) The tallest among them plays Basket ball. (iv) The shortest among them plays Volley ball. (v) Q and S neither play Volley ball nor Basket ball. (vi) R plays Volley ball. (vii) T is between Q who plays Foot ball and P in order of height What does S play? |
|
Answer» Cricket Since R plays Volley ball, so R is the shortest. Q plays neither Volley ball nor Basket ball, so Q is not the tallest. Thus U is the tallest. ` therefore ` the sequence becomes `U gt Q gt T gt PGT S gt R.` Now T plays Tennis, U, being tallest, plays Basket ball. R plays Volley ball. Q plays Foot ball. Both P and S play either Cricket or Bad minton. S plays either Cricket or Badminton. |
|
| 1300. |
(i) Six friends P, Q, R, S, T and U are members of the club and play a different game of Football, Cricket, Tennis, Basket ball, Badminton and Volley ball.(ii) T who is taller than P and S plays Tennis. (iii) The tallest among them plays Basket ball. (iv) The shortest among them plays Volley ball. (v) Q and S neither play Volley ball nor Basket ball. (vi) R plays Volley ball. (vii) T is between Q who plays Foot ball and P in order of height Who among them plays Basket ball? |
|
Answer» Solution :In TERMS of heights, from the data GIVEN, we find that `T gt P, Tgt S, Q gt T gt P ` Since R plays Volley ball, so R is the shortest. Q plays neither Volley ball nor Basket ball, so Q is not the tallest. THUS U is the tallest. ` therefore ` the sequence becomes `U gt Q gt T gt Pgt S gt R.` Now T plays Tennis, U, being tallest, plays Basket ball. R plays Volley ball. Q plays Foot ball. Both P and S play either Cricket or Bad minton. U plays Basket ball. |
|