InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1401. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have no face painted? |
|
Answer» Solution :In this QUESTION X = 10 and x = 2 Such cubes are `(X/x-2)^(3)=3^(3)=27`. |
|
| 1402. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have three faces painted? |
|
Answer» Solution :In this QUESTION X = 10 and x = 2 There are 8 such CUBES. |
|
| 1403. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have only two faces painted? |
|
Answer» 18 Such cubes are `12(10/2-2)=12xx3=36`. |
|
| 1404. |
If 'A' is an event of a random experiment, such that P(A):P(bar(A))=1:2, find the value of P(bar(A)) |
|
Answer» |
|
| 1405. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have two faces painted red and black and all other faces unpainted? |
|
Answer» 36 Such CUBES are `1/3[12(10/2-2)]=1/3xx36=12`. |
|
| 1406. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have three faces painted with different colours? |
|
Answer» 0 |
|
| 1407. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have two faces black? |
|
Answer» 27 There can be no such cube which has two of its FACES both PAINTED with the same colour. |
|
| 1408. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have only one face painted red and all other faces unpainted? |
|
Answer» 18 Such CUBES are `1/3[6(10/2-2)^(2)]=1/3xx54=18` |
|
| 1409. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes are there in all? |
|
Answer» 250 There are `(10/2)^(3)` i.e. 125 CUBES in all. |
|
| 1410. |
A solid cube of each side 10 cm, has been painted red, blue and black on pairs of opposite faces. It is then cut into cubical blocks of each side 2 cm. Answer the following questions. How many cubes have one face painted blue and one face painted red? |
|
Answer» 18 |
|
| 1411. |
Find the sum of the first 22 terms of the A.P. : 8, 3, -2,…………. |
|
Answer» |
|
| 1412. |
If the radii of two concentric circles are 4 cm and 5 cm, then find the length of each chord of one circle which is tangent to the other circle. |
| Answer» Solution :Length of Tangent`= 2 xx sqrt(5^(2) - 4^(2)) = 2xx 3 CM = 6CM` | |
| 1413. |
Out of 400 bulbs in a box, 15 bulbs are defective. One bulb is taken out at random from the box. Find the probability that the drawn bulb is not defective. |
|
Answer» |
|
| 1414. |
You have studied in Class IX, (Chapter 9, Example 3), that a median of a triangle divides it into two triangles of equal areas. Verify thisresult for Delta ABC whose vertices are A(4,-6), B(3,-2) and C(5,2) |
|
Answer» |
|
| 1415. |
If matrix X=[{:(,-3,4),(,2,-3):}] [{:(,2),(,-2):}] and 2X-3Y=[{:(,10),(,-8):}] find the matrix 'X' and matrix Y. |
|
Answer» |
|
| 1416. |
Find the value of 'k' if (x-2) is a factor of x^3+2x^2-kx+10. Hence determine whether (x+5) is also a factor. |
|
Answer» |
|
| 1417. |
Find the area of the quadrilateral whose vertices,taken in order, are (-4, -2), (-3, -5), (3,-2) and (2,3) |
|
Answer» |
|
| 1418. |
How much should a man invest in 80rs shares selling at 75rs to obtain an annual income of 1080rs , if the dividend declared is 15 percent ? |
|
Answer» |
|
| 1421. |
A right circular cone is divided into three parts by trisecting its height by two planes drawn parallel to the base. Show that the volumes of the three portions starting from the top are in the ratio 1 : 2 : 19. |
| Answer» | |
| 1422. |
Name the type of quadrilateral formed, if any, by the points, and give reasons for your answer. (-3, 5), (3, 1), (1, -3), (-5, 1) |
|
Answer» |
|
| 1423. |
Find the ratio in which the point (-3,p) divides the line joiningthe points (-5,-4) and (-2,3) .Hence find the value of p . |
|
Answer» |
|
| 1424. |
In the given figure , DEFG is a square and angleBAC= 90^(@)prove that(i) triangleAGF~ triangleDBG(ii) triangleAGF~triangleEFC |
|
Answer» Solution :(i) Since `squareDEFG` is a SQUARE GF||BC `Rightarrow angle2 = angle4 and angle6 = angle9`( CORRESPONDING ` angles`) Now in ` triangle AGF and triangle DBG` `angle5 = angle1`( each `90^(@)`) ` angle4 =angle2 ` (corrersponding `angles`) 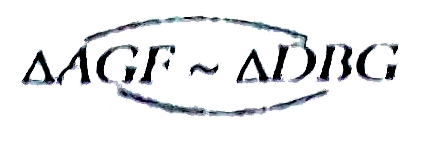 ( AA corollary Hence proved.) ( AA corollary Hence proved.)(ii) In `triangleAGF and triangleDBC,` `angle5 = angle8 ("each" 90^(@))` `angle4 = angle2` ( corresponding `angles`)  ( AA corollary) ( AA corollary)(iii) since `triangleAGF ~ triangleDBG` [proved in (i)] and `triangleAGF~triangleEFC` [ proved in (ii)] `triangleAGF ~ triangleDBG~triangleEFC`Hence proved. Now since  `(DB)/(EF) = (DG)/(EC) ` (corrsponding sides of similar `triangles` are proportional) `Rightarrow DGxx EF= BD xx EC` `Rightarrow DExx DE= BD xx EC` ( DG= FE= DE being the sides of sqaure) `DE^(2)= BD xx EC` BUT If we have to prove only the fourth part i.e. prove that `DE^(2) = BD xx EC` then no need to prove first TWO parts. For `DE^(2)= BD xx EC` , we need to provetwo `triangles` similar which contains DE, BD andEC. Obviously, these are ` triangle GBD and triangleFEC`. `{:(angle1=angle8 ""("each "90^(@)),|,"Searching for second Angles"),(,"As we know that" angle5=90^(@),),(,"Also," angle2+angle9=90^(@)("angle sum property")....(1),),(,:."""Also Since"angle1=90^(@),),(,angle2+ANGLE3=90^(@)"(angle sum property)...(2)",),(,:. "From (1) and (2) , We get " ,),(,rArr "" angle2+angle3=angle2+angle9 ""(each 90^(@)),),(,rArr "" angle3=angle9,):}` Now in `triangleGBD and triangleFEC`. `angle1 = angle8( each 90^(@))` `angle3 = angle9` ( just proved)  ( AA corollary) ( AA corollary) ` DG xxEF= BD xx EC` `DExx DE = BD xx EC ` ( DG = EF = DF , sides of a square) `Rightarrow DE^(2) = BD xx EC`Hence proved. |
|
| 1425. |
A die is thrown once . What is the probability of getting anumber lying between 2 and 6 ? |
|
Answer» `(1)/(2)` |
|
| 1426. |
Construct a rectangle of 2.2 cm and 4.4 cmand then construct a square of area of the drawn rectangle and also find the length of each sides of those squares. |
|
Answer» |
|
| 1427. |
An honest person invested some amount at the rate of 12% simpleinterestand someotheramount at the rate of 105simple interest. He received yearly interestof₹ 130. But if he had interchanged amount invested,he would have received₹ 4 more as interest .Howmuch amountdid he invest at differentrates. ?(ii)Whichmathematicalconceptis used in this problem.?(iii)Whichvalueis beingemphasized here ? |
|
Answer» (ii)Pairof linearequation in two variables. (iii)Honesty isthe BEST policy. |
|
| 1428. |
Find the sum of G.P. : 1-(1)/(2)+(1)/(4)-(1)/(8)+ . . . .. . . .. .to 9 terms . |
|
Answer» |
|
| 1429. |
Find, in each case, the remainder when : (i) x^(4)- 3x^2 + 2x + 1 is divided by x - 1. (ii) x^2 + 3x^2 - 12x + 4 is divided by x - 2. (iii) x^4+ 1 is divided by x + 1. |
|
Answer» |
|
| 1430. |
A statue, 1.6 m stands on the top of a pedestal. From a point on the ground, the angle of elevation of the top of the statue is 60^(@) and from the same point the angle of elevation of the top of the pedestral is 45^(@). Find the height of the pedestral. |
|
Answer» |
|
| 1432. |
Solve the quadratic equation by Completing the Square: 4x^(2)+3x-5=0 |
|
Answer» |
|
| 1433. |
Prove that if x and y are both odd positive intergers thenx^(2) +y^(2)is even but not divisible by 5. |
| Answer» | |
| 1434. |
If in equation a_(1)x+b_(1)y+c_(1)=0 and a_(2)x+b_(2)y+c_(2)=0(a_(1))/(a_(2)) =(b_(1))/(b_(2))ne(c_(1))/(c_(2)) then which of the following is true? |
|
Answer» INTERSECTING LINES |
|
| 1435. |
State with reason, whether the following are true of false. A, B and C are matrices of order 2 xx 2. A^2-B^2=(A+B) (A-B) |
|
Answer» |
|
| 1436. |
Saraswati college purchase a computer for their lab. The discount of 10% was given on the printed price of computer. Rate of GST charged was 18%. Purchase price for computer is 47,790. Find the printed on computer. |
|
Answer» |
|
| 1437. |
Constructa right-angledtriangle ,the hypotenuseof which is 11. 4 cmand thelengthof anothersideis 9 cm . Then byconstructingthe incricleof thistrianglefindthe inradiusof it. |
|
Answer» |
|
| 1438. |
If a=x(y-z), b=y(z-x) and c= z(x-y) What is the value of (xyz)/( abc) ((a^3)/( x^3) + (b^3)/( y^3) + (c^3)/( z^3) )? |
|
Answer» |
|
| 1439. |
Find the annual income derived from an investment of Rs. 18,000 in Rs. 150 shares available at Rs. 180 of a company paying11% dividend. |
|
Answer» |
|
| 1440. |
Neha went to a 'sale' to purchase some pants and skirts. When her friend asked her how many of each she had bought, she answered "The number of skirts are two less than twice the number of pants purchased. Also the number of skirts is four less than four times the number or pants purchased." Help her friends to find how many pants and skirts Neha bought. |
|
Answer» |
|
| 1441. |
Write the median class of the following distribution: |
|
Answer» |
|
| 1442. |
A train covers a distance of 360 km at a uniform speed. Had the speed been 5km/hour more, it would have taken 48 minutes less for the journey. Find the original speed of the train |
|
Answer» SOLUTION :Let the ORIGINAL speed of the train be x km/h `therefore (360)/(x) -(360)/(x+5) = (48)/(60)` `RARR x^(2) + 5 x - 2250 =0` `rArr (x+ 50) 9x-45) =0 therefore x = 45` Hence original speed of the train = 45km/h |
|
| 1443. |
For which of the following values of x is8^(1+sinx + sin^(2)x + sin^(3)x + … + oo) = 64 ? |
|
Answer» `60^(@)` (ii) Equate the powers on either SIDES by MAKING equal bases. |
|
| 1444. |
For Uttarakhand flood victims two sections A and B of class X contributed Rs. 1,500. If the contribution of X - A was Rs. 100 less than that of X - B, find graphically the amounts contributed by both the sections. |
|
Answer» |
|
| 1445. |
If they are in G.P.Write next one terms. x,1,1/x,......... (x ne 0) |
| Answer» | |
| 1447. |
If the point (x, y) is equidistant from the point (a+b,b-a) and (a-b,a+b), then which of the following is correct ? |
|
Answer» `ax=by` |
|
| 1448. |
Choose the best alternative as the answer- A scenery always has |
|
Answer» Paints |
|
| 1449. |
If the sum of the first 14 terms of an AP is 1050 and its first term is 10, find the 20th term. |
|
Answer» |
|
| 1450. |
The mode of the following distributiontable is 15. Find the mean of this data, and then find the median value by using empirical formula relating mean, median and mode. |
|
Answer» |
|