InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
In the given figure , DEFG is a square and angleBAC= 90^(@)prove that(i) triangleAGF~ triangleDBG(ii) triangleAGF~triangleEFC |
|
Answer» Solution :(i) Since `squareDEFG` is a SQUARE GF||BC `Rightarrow angle2 = angle4 and angle6 = angle9`( CORRESPONDING ` angles`) Now in ` triangle AGF and triangle DBG` `angle5 = angle1`( each `90^(@)`) ` angle4 =angle2 ` (corrersponding `angles`) 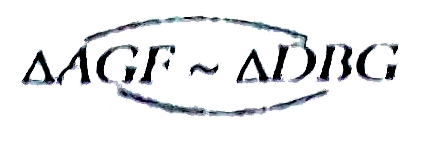 ( AA corollary Hence proved.)(ii) In `triangleAGF and triangleDBC,` `angle5 = angle8 ("each" 90^(@))` `angle4 = angle2` ( corresponding `angles`)  ( AA corollary)(iii) since `triangleAGF ~ triangleDBG` [proved in (i)] and `triangleAGF~triangleEFC` [ proved in (ii)] `triangleAGF ~ triangleDBG~triangleEFC`Hence proved. Now since  `(DB)/(EF) = (DG)/(EC) ` (corrsponding sides of similar `triangles` are proportional) `Rightarrow DGxx EF= BD xx EC` `Rightarrow DExx DE= BD xx EC` ( DG= FE= DE being the sides of sqaure) `DE^(2)= BD xx EC` BUT If we have to prove only the fourth part i.e. prove that `DE^(2) = BD xx EC` then no need to prove first TWO parts. For `DE^(2)= BD xx EC` , we need to provetwo `triangles` similar which contains DE, BD andEC. Obviously, these are ` triangle GBD and triangleFEC`. `{:(angle1=angle8 ""("each "90^(@)),|,"Searching for second Angles"),(,"As we know that" angle5=90^(@),),(,"Also," angle2+angle9=90^(@)("angle sum property")....(1),),(,:."""Also Since"angle1=90^(@),),(,angle2+ANGLE3=90^(@)"(angle sum property)...(2)",),(,:. "From (1) and (2) , We get " ,),(,rArr "" angle2+angle3=angle2+angle9 ""(each 90^(@)),),(,rArr "" angle3=angle9,):}` Now in `triangleGBD and triangleFEC`. `angle1 = angle8( each 90^(@))` `angle3 = angle9` ( just proved)  ( AA corollary) ` DG xxEF= BD xx EC` `DExx DE = BD xx EC ` ( DG = EF = DF , sides of a square) `Rightarrow DE^(2) = BD xx EC`Hence proved. |
|