Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

101.

If the soil obtained by digging holes of breadth 10 metres around the four outside of a cuboidal land of length 240 metres and of breadth 180 metres, be strewed upon the whole land, then the height of the land is increased by 25 cm. Find the height of the hole.

Answer»


ANSWER :350 sq-cm
Discussion
102.

Statements: 1. All men are boys. 2. All boys are students. Conclusions: 1. Some boys are men. 2. Some students are boys.

Answer»

SOLUTION :CLEARLY from the Venn-diagram, both the CONCLUSIONS HOLD.
Discussion
103.

In triangleABC, AD, BE, CF are the medians. Prove that, 4(AD^(2)+BE^(2)+CF^(2))= 3(AB^(2)+BC^(2)+AC^(2)).

Answer»


ANSWER :`4(AD^(2)+BE^(2)+CF^(2))= 3(AB^(2)+BC^(2)+AC^(2))`
Discussion
104.

The upper part of a tree broken over by the wind makes an angle of 30^(@) with the ground and the distance of the root from the point where the top touches the ground is 25 m. What was the total height of the tree?

Answer»


ANSWER :43.3 m
Discussion
105.

Two dice are rolled simultaneously. Find the probability of : obtaining a total of at least 9.

Answer»


ANSWER :`5/18`
Discussion
106.

c - b ba -cab-ac-ab-ac

Answer»

abcbc
acbcb
BABC c
bcacb

Solution :The SERIES is `cab//bac//cab//bac//cab//bac`
THUS the pattern cab bac is REPEATED.
Discussion
107.

Draw the graph of the following equations and answer the following questions : x + y = 5x - y = 5(i) Find the solution of the equation from the graph. (ii) Shade the triangular region formed by the lined and the y-axis.

Answer»


ANSWER :Correct graph and solution is ( 5,0) , SHADE the required REGION.
Discussion
108.

Iftriangle ABC~trianglePQR and (AB)/(PQ)=(7)/(5), then………..

Answer»

`TRIANGLEABC` is BIGGER
`TRIANGLE PQR` is bigger
both TRIANGLES will be equal
can not be decided

Answer :A
Discussion
109.

Find the area of the corresponding major sector of a circle of radius 28 cm and the central angle 45^(@) .

Answer»


ANSWER :2156 `CM^(3)`
Discussion
110.

Prove that if chords of congruent circles subtend equal angles at their centres then chords are equal.

Answer»


ANSWER :DE=AB
Discussion
111.

The midpoints of sides of a triangle are (3, 4), (4, 1) and (2, 0). Which of the following does not devote the co-ordinates of its verities ?

Answer»

1, 3
5, 3
5, 5
3, -3

Answer :B
Discussion
112.

The radii of circular ends of a solid frustum of a cone are 33 cm and 27 cm and its slant height is 10 cm. Find its volume and total surface area.

Answer»


ANSWER :`22,704 CM^(3), (53196)/(7) cm^(2)`
Discussion
113.

The sum of digits of a two digit number is 7. If the digits are reversed and the resulting number is decreased by 2, twice the original number is obtained, find the original no. OR A boat takes 5 hours to go 300 km down stream. It takes the same time to go 150 km upstream. Calculate, (i) the speed of the boat in still water. (ii) the speed of the stream.

Answer»


ANSWER :`:.` The original NUMBER `=yx=25`
OR
`:.` Speed of the BOAT in STILL water is 45km/hr.
Speed of the STREAM is 15km/hr.
Discussion
114.

Find the common difference of the AP in which 18th term is 10 less than the 20th term.

Answer»


ANSWER :`2D = 10 RARR d = (10)/(2) = 5`.
Discussion
115.

Which of the following is false?

Answer»

`{1} in A`
`{1,2} subseteq A`
`{1,2} in A`
None

Answer :D
Discussion
116.

Name the type of quadrilateral formed, if any by the following points, and give reasons for your answer : (4, 5),(7, 6), (4, 3), (1, 2)

Answer»


ANSWER :PARALLELOGRAM
Discussion
117.

is 3x(2x-5)+6=2x(3x+5)-6 a quadratic equation ?

Answer»


ANSWER :GIVEN EQUATION is not a QUADRATIC equation.
Discussion
118.

What kind of a polynomial is l(x) ?

Answer»


ANSWER :Linearpolynomial .
Discussion
119.

Complete the sequence ac - cab - baca - aba - acac

Answer»

aacb
acbc
babb
bcbb

Solution :The SERIES is a C a c / a B a b / a c a c / a b a b / a c a c
Discussion
120.

Draw a less than cumuative frequency curve (ogive) for the following distribution :

Answer»

Solution :The cumulative frequecny table for the given DISTRIBUTION is :
WIDTH="80%"> LTBR Taking upper class limits along X-axis and corresponding cumulative frequencies along Y-axis mark the points (10,7), (15,16), (20,28),(25,36) and (30,42). Join the points marked by a free hand curve (as shown in figure)
`(#NTN_MATH_X_C14_S01_033_S02.png" width="80%">
Discussion
121.

Cards on which numbers 1, 2, 3 .......... 100 are written (one number on one card and no number is repeated), put in a bag and are mixed thoroughly. A card is drawn at random from the bag. Find the probability that card taken out has What is the probability that card taken out has a odd number ?

Answer»

0.25
0.49
`0.50`
0.51

Solution :There are 100 cards in bags. THUS we have 100 possible outcomes for all cases.
`N(S)=100`
Odd NUMBERS 1 to 100 are 50.
NUMBER of favourable outcomes,
`n(E_(1))=50`
P(an odd number),
`P(E_(1))=(n(E_(1)))/(n(S))=(50)/(100)=(1)/(2)`
Thus ( c ) is correct option.
Discussion
122.

Cards on which numbers 1, 2, 3 .......... 100 are written (one number on one card and no number is repeated), put in a bag and are mixed thoroughly. A card is drawn at random from the bag. Find the probability that card taken out has What is the probability that card taken out has a two digit odd number ?

Answer»

0.23
0.45
0.56
0.34

Solution :TOTAL odd number are 50 and 5 numbers are one digit odd number. Hence TWO digit odd number are 45. Thus favourable OUTCOMES,
`n(E_(2))=50-5=45`
P(Two digit odd number),
`P(E_(2))=(n(E_(2)))/(n(S))=(45)/(100)=0.45`
Thus (b) is CORRECT option.
Discussion
123.

Cards on which numbers 1, 2, 3 .......... 100 are written (one number on one card and no number is repeated), put in a bag and are mixed thoroughly. A card is drawn at random from the bag. Find the probability that card taken out has What is the probability that card taken out has a odd number which is multiple of 11?

Answer»

<P>0.05
0.1
0.12
0.06

Solution :Favourable outcomes are {11, 33, 55, 77, 99}. Number of favourable outcomes is 5. Therefore
`n(E_(3))=5`
P(odd number MULTIPLE of 11),
`P(E_(3))=(n(E_(3)))/(n(S))=(5)/(100)=0.05`
Thus (a) is correct option.
Discussion
124.

Cards on which numbers 1, 2, 3 .......... 100 are written (one number on one card and no number is repeated), put in a bag and are mixed thoroughly. A card is drawn at random from the bag. Find the probability that card taken out has What is the probability that card taken out has an odd number which is not less than 70 ?

Answer»

<P>0.13
0.14
0.12
0.15

Solution :Favourable outcomes are 71, 73, 75, …….99.
NUMBER of favourable outcomes, `n(E_(4))=15`
P(odd number not LESS than 70),
`P(E_(4))=(n(E_(4)))/(n(S))=(15)/(100)=0.15`
Thus (d) is correct option.
Discussion
125.

Cards on which numbers 1, 2, 3 .......... 100 are written (one number on one card and no number is repeated), put in a bag and are mixed thoroughly. A card is drawn at random from the bag. Find the probability that card taken out has What is the probability that card taken out has an odd number which is not multiple of 11 ?

Answer»

<P>0.25
`0.50`
`0.40`
`0.45`

Solution :Total odd number are 50 and out of which {11, 33, 55, 77, 99} are multiple of 11. Thus 50 - 5 = 45 NUMBERS are multiple of 11.
Therefore `""n(E_(5))=45`
P(odd number not multiple of 11),
`P(E_(5))=(n(E_(5)))/(n(S))=(45)/(100)=0.45`
Thus (d) is correct option.
Discussion
126.

If numbers n- 2, 4n -1 and 5n + 2 are in A.P. find the value of n and its next two terms.

Answer»


ANSWER :n=1 and A.P.=-1,3,7,11,15,…
Discussion
127.

The radius of the base and the height of a right circular cone are 7 cm and 24 cm respectively. Find the volume and the total surface area of the cone.

Answer»


ANSWER :`704 CM ^(2)`
Discussion
128.

P^^Q means (P+Q)/(Q-P)andPvvQ means (Q-P)/(Q+P) Answer the following questions: 6^^4+4vv6

Answer»

`24/5`
`-24/5`
`26/5`
`-26/5`

ANSWER :A
Discussion
129.

The mean of the following frequency distribution is 50 :

Answer»


ANSWER :10
Discussion
130.

517, 661, 814, 922, 1066, 1256

Answer»

661
814
1256
922

Solution :SUM of the INTEGERS in each NUMBER is 13,
Discussion
131.

Draw a line segment of length 7.2 cm and divide it in the ratio 5:3 .Measure the two parts.

Answer»


ANSWER :2.7 CM
Discussion
132.

Find the sum of G.P. : 1+3+9+27+ . . . . .. .to 12 terms.

Answer»


ANSWER :`(1)/(2)(3^(12)-1)=265720`
Discussion
133.

If the mean of x and 1/x is M, then the mean of x^(2) and 1/x^(2)is

Answer»

` M^2`
` M^(2)//4`
`2M^(2)-1`
` 2M^(2) + 1`

ANSWER :C
Discussion
134.

If alpha=(4)/(5) and alpha=(4)/(5),then which of the following is true?

Answer»

`alphaltbeta`
`alphalgtbeta`
`alpha=beta`
NONE of these

Solution :FIND `sinbetaand COMPARE SINALPHA and sinbeta`.
Discussion
135.

A and B are brother, C and D are sisters. As son is Ds brother. How is B related to C?

Answer»

Father
BROTHER
Uncle
Grand father

Solution :B is A.s brother and A.s son D.s brother, this means D is the DAUGHTER of A SINCE C and D are sister, C is the daughter of A. So B is the uncle of C
Discussion
136.

Find the mean of the following table by step deviation method :

Answer»

SOLUTION :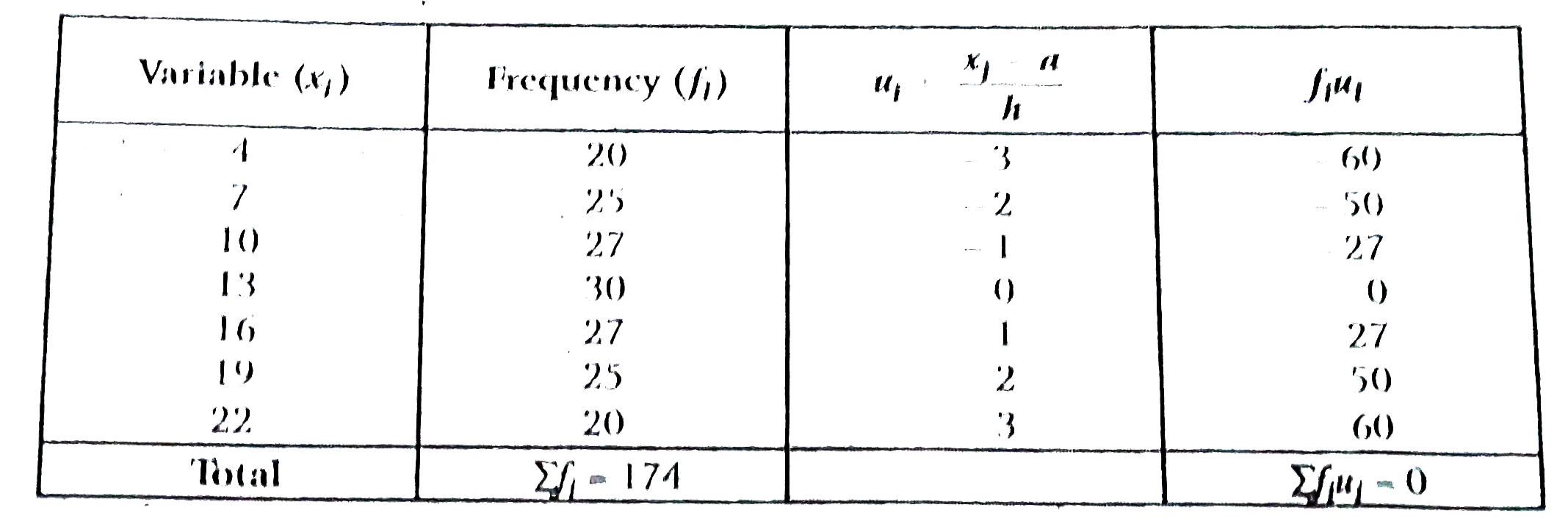
Here, h=3
Let assumed mean a=13
` :."""mean"barx=a+(sumf_(i)*u_(i))/(sumf_(i))xxh=13+(0)/(174)xx3=13`
Discussion
137.

How much should a man invest in 100rs shares selling at 110rs to obtain an annual income of 1680rs, if the dividend declared is 12%

Answer»


ANSWER :`15400rs`
Discussion
138.

If two adjacent vertices of a parallelogramare (3, 2) and (-1, 0) and the diagonals intersect at (2, -5), then find the coordinates of the other two vertices.

Answer»

Solution :Let two ADJACENT vertices of a PARALLELOGRAM are `A-=(3, 2) and B(-1, 0).`
Let coordinates of other two vertices are `C(x_(1), y_(1)) and D(x_(2),y_(2)).`
We KNOW that diagonals of a parallelogram bisect each other.
`therefore` Mid-point of AC and Mid-point of BD are same i.e., point O(2, -5).
`therefore""(3+x_(1))/(2)=2 and (2+y_(1))/(2)=-5`
`rArr""x_(1)=1 and y_(1)=-12 rArrC-=(x_(1), y_(1))-=(1, -12)`
Also, `""(x_(2)-1)/(2)=2 and (y_(2)+0)/(2)=-5`
`rArr""x_(2)=5 and y_(2)=-10rArrD-=(5, -10)`
Hence,remaining vertices are (1, -12) and (5, -10).
Discussion
139.

Can 2n^2+ 7 be the nth term of an A.P. ? Explain.

Answer»


ANSWER :No, (the DIFFERENCE between CONSECUTIVE TERMS is not the same)
Discussion
140.

Determine the value of the following. log_(10).0.01

Answer»


ANSWER :`-2`
Discussion
141.

If a lt 0 then the shape of ax^(2) + bx + c = 0 is …………

Answer»




ANSWER :D
Discussion
142.

Divide 50760rs into two parts such that if one part is invested in 8% 100rs shares at 8% discount and the other in 9% 100rs shares at 8% premium the annual incomes from both the investments are equal

Answer»


ANSWER :`24840rs` and `25920rs`
Discussion
143.

The sum of the height and the radius of a solid cylinder is 35 cm and its total surface area is 3080 cm^(2), find the volume of the cylinder.

Answer»


ANSWER :`12,963 CU. CM`
Discussion
144.

Find the slope of the lines passing through the given points C(5, -2) and D(7, 3)

Answer»


ANSWER :SLOPE `CD = (5)/(2)`
Discussion
145.

Find the area of the shaded region in figure, if ABCD is a square of side 7cm . And APD and BPC are semicircles. (usepi=(22)/(7))

Answer»


ANSWER :`10.5cm^(2)`
Discussion
146.

The ratio in which the line 3x+y=9 divides the line sequent joining the points (1, 3) and (2, 7) is given by

Answer»

`4:3`
`3:4`
`2:3`
`3:2`

ANSWER :B
Discussion
147.

If a,b and c are A.P. whereas x,y and z are in G.P. : Prove that : x^(b-c)*y^(c-a)*z^(a-b)=1.

Answer»


ANSWER :1
Discussion
148.

The probability of getting a prime number when a die is thrown once is (2)/(3).

Answer»


ANSWER :FALSE, it is `(1)/(2)`
Discussion
149.

If A=[{:(,2,1,-1),(,0,1,-2):}] find: (i) A^(t).A (ii) A.A^(t) where A^t is the transpose of matrix A.

Answer»


ANSWER :`(i) [{:(,4,2,-2),(,2,2,-3),(,-2,-3,5):}]` (II) `[{:(,6,3),(,3,5):}]`
Discussion
150.

Mr. Ram Gopal invested 8000rs in 7% 100rs shares at 80rs. After a year, he sold these shares at 75rseach and invested the proceeds (including hisdividend ) in 18%, 25rs shares at 41rs .Find (i) his dividend for the first year (ii) his annual income in the second year (iii) the percentage increase in his return on his original investment.

Answer»


ANSWER :`(i) 700rs` (II)900RS` `(III) 2.5%`
Discussion