Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

151.

Find the A.P. whose 6th term =5 and 10th term=9

Answer»


ANSWER :0,1,2,3,4,5
Discussion
152.

In a bucket and ball race, a bucket is placed at the starting point, which is 5 m from the first ball, and the other balls are placed 3 m apart in a straight line. There are ten balls in the line. A competitor starts from the bucket, picks up the nearest ball, runs back with it, drops it in the bucket, runs back to pick up the next ball, runs to the bucket to drop it in, and she continues in the same way until all the balls are in the bucket. What is the total distance the competitor has to run? (Hint: To pick up the first ball and the second ball, the total distance (in metres) run by a competitor is 2 x 5 + 2 x (5+3)]

Answer»


ANSWER :370
Discussion
153.

If B and C are two matrices such that B=[{:(,1,3),(,-2,0):}] and C=[{:(,17,7),(,-4,-8):}], find the matrix M so that BM=C.

Answer»


ANSWER :`[{:(,2,4),(,5,1):}]`
Discussion
154.

Evalutate: [{:(,2cos 60^@, -2sin 30^@),(,-tan 45^@,cos 0^@):}] [{:(,cot 45^@, cosec 30^@),(,sec 60^@, sin 90^@):}]

Answer»


ANSWER :`[{:(,-1,1),(,1,-1):}]`
Discussion
155.

A metallic sphere of radius 10.5 cm is melted and then recast into small cones each of radius 3.5 cm and height 3 cm. Find the number of cones thus formed.

Answer»


ANSWER :`126`
Discussion
156.

Solve the following pairs of equations (i) x + y = 3.3, "" (0.6)/(3x - 2y) = -1, 3x - 2y != 0 (ii)(x)/(3) + (y)/(4) = 4, "" (5x)/(6) - (y)/(8) = 4 (iii) 4x + (6)/(y) = 15, "" 6x - (8)/(y)= 14, y != 0 (iv) (1)/(2x) - (1)/(y) = -1, "" (1)/(x) + (1)/(2y) = 8, x, y != 0 (v) 43x + 67y = -24, "" 67x + 43y = 24 (vi) (x)/(a) + (y)/(b) = a + b , "" (x)/(a^(2)) + (y)/(b^(2)) = 2, a, b != 0 (vii) (2xy)/(x+y) = (3)/(2), "" (xy)/(2x-y) = (-3)/(10), x + y != 0, 2x - y != 0

Answer»

Solution :(i) Given pair of linear equations are is
`" " x+y=3.3 " " ...(i)`
and `{:(ul(" "0.6" ")),(3x-2y):}=-1`
`rArr 0.6=-3x+2y`
`rArr " " 3x-2y=-0.6 "" ...(ii)`
Now, MULTIPLYING Eq. (i) by 2 and then adding with Eq. (ii), we get
`rArr " " 2x+2y=6.6`
`rArr " " 3x-2y=-0.6`
`"" 5x=6 rArr x=(6)/(5)=1.2`
Now, PUT the value of x in Eq. (i) , we get
`" " 1.2+y=3.3`
`rArr " " y=3.3 -1.2`
`rArr " " y=2.1`
Hence, the required values of x and y are 1.2 and 2.1, respectively.
(ii) Given, pair of linear equations is
`" " (x)/(3)+(y)/(4)=4`
On multiplying both sides by LCM (3, 4)=12, we get
4X+3y=48`"" ...(i)`
and `(5x)/(6)-(y)/(8)=4`
On multiplying both sides by LCM (6, 8)=24, we get
`20x-3y=96 " " ...(ii)`
Now, adding Eqs. (i) and (ii), we get
`" " 24x=144`
`rArr " " x=6`
Now, put the value of x in Eq. (i) , we get
`4xx6+3y=48`
`rArr " " 3y=48-24`
`rArr " " 3y=24 rArr y=8`
Hence, the required values of x and y are 6 and 8, respectively.
(iii) Given, pair of linear equations are
` 4x+(6)/(y)=15 " "...(i)`
and `" " 6x-(8)/(y)=14, y != 0 " " ...(ii)`
Let `u=(1)/(y)`, thenabove equation becomes
`4x+6u=15 " " ... (iii)`
and `" " 6x-8u=14 " " ...(iv)`
On multiplying Eq. (iii) by 8 and Eq. (iv) by 6 and then adding both of them, we get
`32x+48u=120`
`36x-48u=84 rArr 68x=204`
`rArr "" x=3`
Now, put the value of x in Eq. (iii), we get
`" " 4xx3+ 6u=15`
`rArr " " 6u=15-12 rArr 6u=3`
`rArr " " u=(1)/(2)rArr(1)/(y)=(1)/(2) " " `[`:'u=(1)/(y)`]
`rArr "" y=2`
Hence, the required values of x and y are 3 and 2, respectively.
(iv) Given pair of linear equations is
`(1)/(2x)-(1)/(y)=-1 "" ...(i)`
and `" " (1)/(x)+(1)/(2y)=8,x,y!=0 " " ...(ii)`
Let ` u=(1)/(x)` and `v=(1)/(y)`, then the above equations becomes
`(u)/(2)-v=-1`
`rArr " " u-2v=-2 "" ...(iii)`
and `" " u+(v)/(2)=8`
`rArr " " 2u+v=16 "" ...(iv)`
On, multiplying Eq. (iv) by 2 and then adding with Eq. (iii), we get
`{:(4u+2v=32),(ul(u-2v=-2)),("" 5u=30):}`
`rArr "" u=6`
Now, put the value of u in Eq. (iv), we get
`2xx6+v=16`
`rArr " " v=16-12=4`
`rArr " " v=4`
`:. " " x=(1)/(u)=(1)/(6)` and `y=(1)/(v)=(1)/(4)`
Hence, the required values of x and y are `(1)/(6)` and `(1)/(4)`, respectively.
(v) Given pair of linear equations is
`43x+67y=-24 " " ...(i)`
and `" " 67x+43y=24 "" ...(ii)`
On multiplying Eq. (i) by 43 and Eq. (ii) by 67 and then subtracting both of them, we get
`{:((67)^(2)x+43xx67y=24xx67),(ul(underset(-)((43))^(2)x+underset(-)43xx67y=-underset(+)24xx43)),({(67)^(2)-(43)^(2)}x=24(67+43)):}`
`rArr " " (67+43)(67-43)x=24xx110 "" `[`:' (a^(2)-b^(2))=(a-b)(a+b)`]

`rArr " " 110xx24x=24xx110`
`rArr "" x=1`
Now, put the value of x in Eq. (i), we get
`43xx1+67y=-24`
`rArr " " 67y=-24-43`
`rArr " " 67y=-67`
`rArr "" y=-1`
Hence, the required values of x and y and 1 and -1, respectively.
(vi) Given pair of linear equations is
`(x)/(a)+(y)/(b)=a+b "" ...(i)`
and `" " (x)/(a^(2))+(y)/(b^(2))=2, a, b!=0 "" ...(ii)`
On multiplying Eq. (i) by `(1)/(2)` and then subtracting from Er. (ii) , we get
`{:((x)/(a^(2))+(y)/(b^(2))=2),(ul((x)/underset(-)(a^(2))+(y)/underset(-)(ab)=underset(-)1+(b)/(a))),(y((1)/(b^(2))-(1)/(ab))=2-1-(b)/(a)):}`
`rArr " " y((a-b)/(ab^(2)))=1-(b)/(a)=((a-b)/(a))`
`rArr " " y=(ab^(2))/(a)rArry=b^(2)`
Now, put the value of y in Eq. (ii), we get
`(x)/(a^(2))+(b^(2))/(b^(2))=2`
`rArr " " (x)/(a^(2))=2-1=1`
`rArr "" x=a^(2)`
Hence, the required values ofx and y are `a^(2) ` and `b^(2)`, respectively.
(vii) Given pair of equations is
`(2xy)/(x+y)=(3)/(2)`, where `x+y !=0`
`rArr " " (x+y)/(2xy)=(2)/(3)`
`rArr " " (x)/(xy)+(y)/(xy)=(4)/(3)`
`rArr " " (1)/(y)+(1)/(x)=(4)/(3) "" ...(i)`
and `" " (xy)/(2x-y)=(-3)/(10)`, where `2x-y!=0`
`rArr " " (2x-y)/(xy)=(-10)/(3)`
`rArr " " (2x)/(xy)-(y)/(xy)=(-10)/(3)`
`rArr " " (2)/(y)-(1)/(x)=(-10)/(3)`
Now, put `(1)/(x)=u` and `(1)/(y)=v`, then the pair of equations becomes
`v+u=(4)/(3) "" ...(iii)`
and `" " 2v-u=(-10)/(3) " " ...(iv)`
On adding both equations, we get
`3v=(4)/(3)-(10)/(3)=(-6)/(3)`
`rArr " " 3v=-2`
`rArr" "v=(-2)/(3)`
Now, put the value of v in Eq. (iii), we get
`(-2)/(3)+u=(4)/(3)`
`rArr " " u=(4)/(3)+(2)/(3)=(6)/(3)=2`
`rArr " " x=(1)/(u)=(1)/(2)`
and `" " y=(1)/(v)=(1)/((-2//3))=(-3)/(2)`
Hence, the required values of x and `(1)/(2)`and `(-3)/(2)`, respectively.
Discussion
157.

If sin (A+B) =1 and cos (A-B) = (sqrt(3))/(2), then find the values of A and B.

Answer»

Solution :Given that , `SIN (A+B)=1`
`sin(A+B)=sin90^(@) rArr A+B =90^(@)`…(1)
and`cos(A-B)=(SQRT(3))/(2)`
`rArrcos(A-B)=COS30^(@)rArrA-B=30^(@)`...(2)
Adding equations (1)and (2)
`A+B=90^(@)A-B=30^(@)`
`2A=120^(@)rArr A=60^(@)`Put A` 60^(@)` in equation (1)
`60^(@)+B=90^(@)rArrB=90^(@)-60^(@)=30^(@)`
`:.A=60^(@)and B=30^()@`
Discussion
158.

P,Q and R are on AB, BC and AC of the equilateral triangle ABC respectively. AP:PB=CQ:QB=1:2. G is the centroid of the triangle PQB and R is the mid-points of AC. Find BG:GR.

Answer»

`1:2`
`2:3`
`3:4`
`4:5`

Solution :
LET `AB=BC=AC=3x`
`therefore BP=BQ=PQ=2x`
`(because AP:BP=CQ:BQ=1:2)`
As `Delta PRQ and Delta BAC` are equilateral triangle, the centroid of `Delta BPQ` LIES on BR (where BR is median drawn on to AC).
We KNOW that centroid divides the median in the ratio `2:1`.
`therefore BC=(2)/(3)([SQRT(3)(2x)])/(2)=(2sqrt(3x))/(3)`
But `BR=(sqrt((3)))/(2)=(3sqrt(3x))/(2)`
Now `GR=BR-BG`
`=(3sqrt(3x))/(2)-(2sqrt(3x))/(3)=(5sqrt(3x))/(6)`
Now `BC :GR =(2sqrt(3x))/(3):(5sqrt(3x))/(6) =4:5`.
Discussion
159.

A man desires to have an annual income of 36,000 from 18% at a premium of 20%. How much should he invest?

Answer»


ANSWER :RUPES 2,40,000
Discussion
160.

Find the common difference of an AP in which a_(16) - a_(12) = 16.

Answer»


ANSWER :`K=10`
Discussion
161.

An oil funnel made of tin sheet consists of a 10 cm long cylindrical portion attachedto a frustum of a cone .If the total height is 22 cm diameter of the cylindrical portion is 8 cm and the diameter of the top of the funnel is 18 cm find the area of he tin sheet required to make the funnel.

Answer»

Solution :Given oil funnel is combination of a cylinder and a FRUSTUM of a cone .
Also given height of cylinder portion h=10cm
and , radius `r_(2)=(8)/(2)=4cm`
DIAMETER of top of the funnel =18 cm
Radius of top of the funnel `r_(1)=(18)/(2)=9 cm `
Now height of the frustum of cone =22-10=12 cm
Slant height of he frustum l=`sqrt((12)^(2)(9-4)(2))`
`=sqrt(144+25)=sqrt(169)`
l=13 cm
Required AREA of the tin sheet =curved surface area of cylinder portion +curved surface area of the frustum
`=2pir_(2)h+pi(r_(1)+r_(2))l=(22)/(7)[2xx4xx10+(9+4)13]`
`=(22)/(7)(80+169)=(22)/(7)xx249=(5478)/(7)=782(4)/(7) cm^(2)`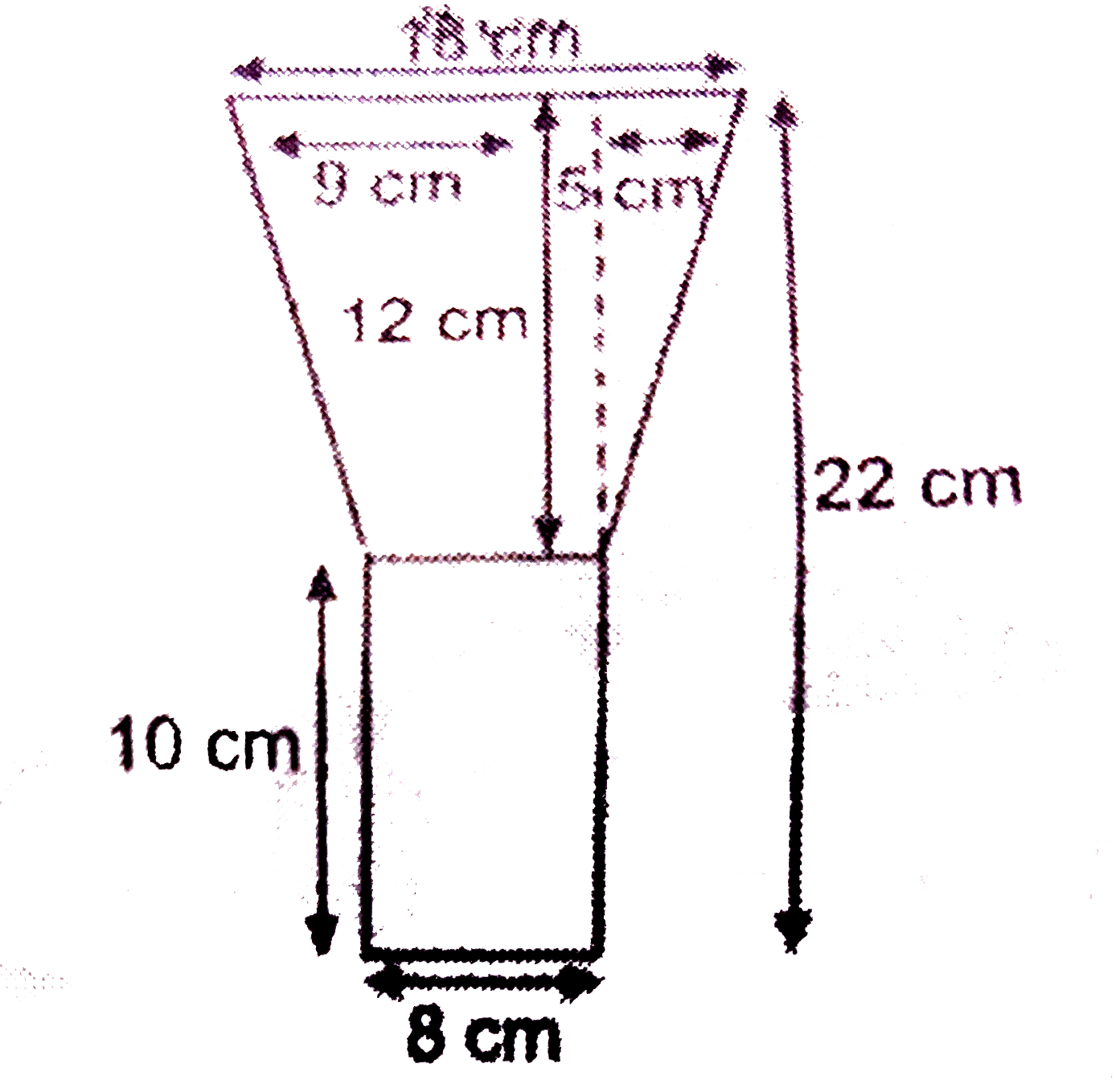
Discussion
162.

How many possibilities are there in each of the following?Vantika Knows the following sites in Maharashtra. She is planning to visit one of them in her summer vacation. Ajintha, Mahabaleshwar, Lonar Sarovar, Tadoba wildlife sanctuary, Amboli, Raigad, Matheran, Anandavan.

Answer»

Solution :Vantika Knows the FOLLOWING SITES in Maharashtra.
She is planning to visit ONE of them in her summer vacation.
Ajintha, Mahabaleshwar, Lonar Sarovar, Tadoba wildlife sanctuary, AMBOLI, Raigad, MATHERAN, Anandavan.
Discussion
163.

Eight metallic spheres, each of radius 2 mm, are melted and cast into a single sphere. Calculate the radius of the new sphere.

Answer»


ANSWER :4 MM
Discussion
164.

Find the values of the sqrt(11) by geometric method .

Answer»


ANSWER :3.3 APPROX.
Discussion
165.

What is the area of the triangle formed by the points (a,c+a),(a,c) and (-a,c-a) ?

Answer»

`a^(2)`
`(1)/(a^(2))`
`a^(2)+a`
zero

Answer :A
Discussion
166.

Two coins are flipped at a gambling stall. A "head" entitles the player to receive Rs 100 while a "tail" imposes a fine of Rs 25. what is the maximum amount that can be won or lost for a single flip of the two coins and what is its probability?

Answer»


ANSWER :`1/4`
Discussion
167.

Construct a Delta ABC such that AB = 5.5 cm, angle C = 25^(@) and the altitude from C to AB s 4 cm.

Answer»


ANSWER :ABC is the REQUIRED TRIANGLE.
Discussion
168.

Prove that : (1+secA)/(secA)=(sin^(2)A)/(1-cosA)

Answer»


ANSWER :`4(3 + SQRT(3))m`
Discussion
169.

If matrix A=[{:(,2,1,3),(,4,-3,2):}] and B=[{:(,3,-2),(,7,4):}], find transpose matrices A^t and B^t. If possible, find (i) A+A^t (ii) B+B^t

Answer»


ANSWER :(i) `A+A^(t)` is not POSSIBLE
(II) `[{:(,6,5),(,5,8):}]`
Discussion
170.

How many squares are there in the figure given below?

Answer»

11
12
13
17

Answer :D
Discussion
171.

Two friends Jack and Jill attend IIT entrance test which has three sections, Mathematics, Physics and Chemistry.Each question in Mathematics, Physics and Chemistry carry 5 marks, 8 marks and 3 marks respectively. Jack attempted 10 questions in Mathematics, 12 in Physics and 6 in Chemistry while Jill attemped 18, 5 and 9 questions in Mathematics, Physics and Chemistry respectively Assuming that all the questions attempted were correct, find the individual marks obtained by the boys by showing the above information asa matrix product.

Answer»


ANSWER :MARKS obtained by Jack = 164
Marks obtained by JILL= 157
Discussion
172.

Two circles with centres O and O' of radii 3 cm and 4 cm, respectively intersect at two points P and Q such that OP and O'P are tangents to the two circles. Find the length of common chord PQ.

Answer»

Solution :PO' is a tangent on circle `C_(1)` at P. OP is tangent on circle `C_(2)` at P. As radius OP and tangent PO' are at a point of contact P.
`:.""angleP=90^(@)`
So, by Pytagoras theorem in right angled `triangleOPO',`
`OO'^(2)=OP^(2)+PQ^(2)=3^(2)+4^(2)=9+16=25 cm`
`implies""OO' = 5 cm`
`triangleOO'P~=triangleOO'Q""`(by SSS criterion of congruence)
`implies""angle1=angle2""`(c.p.c.t.)
`triangleON'P~=triangleON'Q""`(by SAS criterion of congruence)
`implies""angle3=angleO'NQ""`(cpct)
`implies""angle3=angleO'NQ=90^(@)""`(LINEAR pair axiom)
Let `ON=y`, then `NO'=(5-y)`
Let PN = x
By Pythagoras theorem in `trianglePNO` and `trianglePNO', we have
`x^(2)+""y^(2)""=3^(2)""...(1)`{:(,,x^(2),+,y^(2),=3^(2)"........"(i)),(,,x^(2),+,(5-y)^(2),=4^(2)),(x^(2),+,25,+,y^(2)-10y,=16"........"(2)),(,,x^(2),+,y^(2),=9 ["from" (1)]),(,-,,-,,""-):}/`
`25-10y=7""`["SUBTRACT(1) from (2)"]
`implies""-10y=7-25""implies""-10y=-18`
`implies""y=1.8`
But `""x^(2)+y^(2)=3^(2)""`["from (1)"]
`implies""x^(2)+(1.8)^(2)=3^(2)""implies""x^(2)=9-3.24`
`implies""x^(2)=5.76""implies""x=2.4`
`:.` The perpendicular drawn from the centre bisects the chord.
`:.""PQ=2PN=2x=2xx2.4=4.8 cm`
Discussion
173.

If the slant height of a frustum of a conc is 20 cm and the radii of its circular bases are 20 cm and 8 cm respectively, find the volume of the frustum (Use pi=3.14)

Answer»


ANSWER :`10449.92 CM^(3)`
Discussion
174.

A fraction becomes equal to (4)/(5) if 1 is added to both numerator and denominator. If, however, 5 is subtracted from both numerator and denominator, the fraction becomes equal to (1)/(2). What is the fractions?

Answer»


ANSWER :`7/9`
Discussion
175.

Diagonal of a square is 10sqrt2 cm. Find its side.

Answer»


ANSWER :10 CM
Discussion
176.

Check whether the following equations are consistent or inconsistent. Solve them graphically. x+y=5 , 2x+2y=10.

Answer»


ANSWER :INCONSISTENT
Discussion
177.

Points (0,0) ,(3,sqrt(3))and (x,y) from an equilateral triangle , then what is(x,y) ?

Answer»


ANSWER :`(0,2sqrt(3))or (3,-SQRT(3))`
Discussion
178.

If the heightof the cylinder is 9 cm and its radiusof base is 7 cm , then what will be the volume of the cylinder ?

Answer»
Discussion
179.

Find the sum of all natural numbers between 250 and 1000 which are divisible by 9.

Answer»


ANSWER :52542
Discussion
180.

Draw a tangent to a given circle with center O from a point 'R' outside the circle. How many tangents can be drawn to the circle from that point ?

Answer»


ANSWER :TWO
Discussion
181.

Segments AB and CD bisects each other at point M. If A(4,3), B(-2,5), C(-3,5), then find coordinates of D.

Answer»


ANSWER :`(5,3)`
Discussion
182.

A triangleABC is drawnto circumscribe a circleof radius4 cm such thatthe segmentsBD and DC intowhichBC isdivided by thepointof contactD areof lengths8cm and6cm respectivelyas shownin the figure . Findthe sides AB and AC .

Answer»


ANSWER :the side`AC = x+6 = 7 +6 = 13 ` CM
Discussion
183.

Express each of the following numbers as a product of its prime factors. 140

Answer»


ANSWER :`2^(2)xx5xx7`
Discussion
184.

If a+b+ c=0, then is (a^(4) + b^(4) + c^(4) )/( a^(2) b^(2) + b^(2) c^(2) + c^(2) a^(2) ) is equal to

Answer»

4
2
1
16

Answer :B
Discussion
185.

Find the remainder when (26)^(31) is divided by 31.

Answer»


ANSWER :31
Discussion
186.

A cone of height 24 cm and radius of base 6 cm is made of modelling clay. A child reshapes it in the form of a shpere. Find the radius of the sphere.

Answer»


ANSWER :6 CM
Discussion
187.

Ramakanth draws a salary of Rs. 15,000 per month. He contributes Rs. 5000 per month towards PPF. He also donates Rs. 1250 per month towards medical research. Calculate the income tax Ramakanth has to pay.

Answer»


ANSWER :Rs.8400
Discussion
188.

Draw a tangent to the circle from the point P having radius 3.6 cm, and centre at O. Point P is at a distance 7.2 cm from the centre.

Answer»


ANSWER :`=6.2 CM`
Discussion
189.

Eight solid spheres of the same size are made by melting a solid metallic cylinder of diameter 6 cm and height 32 cm. Then, the diameter of each sphere is ......... cm.

Answer»

3
6
12
8
Discussion
190.

Find the next three terms of the sequence : sqrt(5),5,5sqrt(5), . . . . . . . . ..

Answer»


ANSWER :`25,25sqrt(5)" and "125`
Discussion
191.

Find the sum of G.P. : 0*3+0*03+0*003+0*0003+ . . . . . . . to 8 terms.

Answer»


ANSWER :`(1)/(3)(1-(1)/(10^(8)))`
Discussion
192.

How many multiples of 4 lie between 10 and 250?

Answer»


ANSWER :60
Discussion
193.

Let A=[{:(,1,0),(,2,1):}], B=[{:(,2,3),(,-1,0):}]. Find A^2+AB+B^2

Answer»


ANSWER :`[{:(,4,9),(,5,4):}]`
Discussion
194.

Which term of the AP a] 2, 5, 8, ….. is 68? b] -3, -5, -7, ….. is -101? c] 21, 42, 63, …..... is 420? d] 80, 76, 72, …... is 0?

Answer»


Answer :a] `rArr 3n = 69 rArr N = (69)/(3) = 23`.
b] `rArr - 2N = - 100 rArr n = (100)/(2) = 50`.
C] `rArr 21 n = 420 rArr n = (420)/( 21) = 20`.
d] `rArr 4n = 84 rArr n = (84)/(4) = 21.`
Discussion
195.

If A=[{:(,2,-1),(,-1, 3):}]" evaluate "A^2-3A+3I, where I is a unit matrix of order 2.

Answer»


ANSWER :`[{:(,1,-2),(,-2,3):}]`
Discussion
196.

In the given figure find the perimeter of triangleABC.

Answer»


ANSWER :30CM
Discussion
197.

In the given fig AM:DN=4:5 Delta ABC ~ Delta DEF and Area of DeltaDEF=625 cm^(2) The area of Delta ABC is

Answer»

`16 cm^(2)`
`25CM^(2)`
`81 cm^(2)`
`400 cm^(2)`

Answer :B::C::D
Discussion
198.

Solved the following equation by the method of completing the square : 4sqrt3x^(2)+5x-2sqrt3=0

Answer»

Solution :We have, `4sqrt3x^(2)+5x-2SQRT3=0`
Dividing each term by `4sqrt3` we, get
`x^(2)+(5)/(4sqrt3)x=(2sqrt3)/(4sqrt3)=0`
`impliesx^(2)+(5)/(4sqrt3)x=(1)/(2)`
Adding `((1)/(2)"coefficient of x")^(2)i.e.,((5)/(8sqrt3))^(2)` to both SIDES, we get
`x^(2)+(5)/(4sqrt3)x+((5)/(8sqrt(3)))^(2)=((5)/(8sqrt3))^(2)+(1)/(2)`
`implies(x+(5)/(8sqrt3))^(2)=(25)/(192)+(1)/(2)`
`implies(x+(5)/(8sqrt3))^(2)=(25+96)/(192)`
`implies(x+(5)/(8sqrt3))^(2)=(121)/(192)`
Taking square root of both sides, we get
`x+(5)/(8sqrt3)=+-(11)/(8sqrt3)`
`:.x=-(5)/(8sqrt3)+-(11)/(8sqrt3)=(-5+-11)/(8sqrt3)`
`impliesx=(-5+11)/(8sqrt3)orx=(-5-11)/(8sqrt3)`
`impliesx=(3)/(4sqrt3)orx=(-2)/(sqrt3)`
Hence, `x=(3)/(4sqrt3)orx=(-2)/sqrt3)` are the solutions of given equation.
Discussion
199.

Construct a triangle ABC where AB= 6.5 cm , B= 60^(@), and BC = 5.5 cm. Also construct Delta AB'C similar to Delta ABC, whose each side is (3)/(2) times the corresponding side of Delta ABC.

Answer»


ANSWER :`(AB')/(AB ) = (AC ')/( AC ) = (BC ')/( B' C) = (3)/(2)`.
Discussion
200.

The table below the daily expenditure on food of 25 household in a locality. Find the mean dialy expenditure on a food by a suitable method.

Answer»


ANSWER :RS. 211
Discussion