InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2351. |
3080 cm^(3)of water is required to fill a cylindrical vessel completely and 2310 cm ^(3) of water is required to fill it upto 5 cm below the top. Find :wetted surface area of the vessel when it is half-filled with water. |
|
Answer» |
|
| 2352. |
A container , openedfrom the top and made up of a metal sheet, is in the from of a frustum of a cone of height 16 cm with radii of its lower and upper ends as 8 cm and 20 cm respectively . Find the total cost of milk which can completely fill thecontainer at the rate of Rs 20per liter . Also find the cost of metal sheet used to make the conatainer, if it costs Rs 8 per100 cm^(2) |
|
Answer» |
|
| 2353. |
Given cosectheta = (4)/(3), calculate all other trigonometric ratios. |
|
Answer» |
|
| 2354. |
IfA=[(1,-1),(2,-1)],B = [(x,1),(4,-1)] and A^2+B^2=(A+B)^2 find the value of x. State, whether A^2 + B^2 and (A + B)^2are always equal or not. |
|
Answer» |
|
| 2355. |
A triangle ABC is drawn to circumscribe a circle of radius 3cm such that the segments BD and DC into which BC is divided by the point of contact D are of length 9cm. And 3cm. Respectively ( See adjacent figure ). Find the sides AB and AC. |
|
Answer» |
|
| 2356. |
If A=[{:(,3,2),(,0,5):}] and B=[{:(,1,0),(,1,2):}], find : (i) (A+B) (A-B) (ii) A^2-B^2 (iii) Is (A+B) (A-B) =A^2-B^2? |
|
Answer» (II) `[{:(,8,16),(,-3,21):}]` |
|
| 2357. |
Which of the following points are the vertices of an equilateral triangle ? |
|
Answer» `(a,a),(-a,-a),(2a,a)` |
|
| 2358. |
Select the set of numbers in the following, which can form similar triangles. (I) 3, 4, 6 (II) 9, 12, 18 (III) 8, 6, 12 (IV) 3, 4, 9 |
|
Answer» |
|
| 2359. |
If Anil bought a Rs. 150 share at a premium of Rs 20 while Raju brought the same kind of share at a discount of Rs. 20 of the same company, then the dividend erned by Anil is ______ the divident earned by Anis is ______ the dividend earned by Raju. [equal to/less than/more than] |
|
Answer» |
|
| 2360. |
An object is thrown upwards with an initial velocity of 17 m/sec from a building with 12 m height. It is at a height of S = 12 + 17t – 5t^(2) from the ground after a flight of ‘t’ seconds. Find the time taken by the object to touch the ground. |
|
Answer» |
|
| 2361. |
If A(-1,1), B(5, -3), C(3,5) are the vertices of DeltaABC and seg AM is its median find the length of median AM. |
|
Answer» |
|
| 2362. |
Draw a circle of radius 3.5 cm. Mark a point P outside the circle at a distance of 6 cm from the centre. Construct two tangents from P to the given circle. Measure and write down the length of one tangent. |
|
Answer» |
|
| 2363. |
The product of two consecutive natural numbers which are multliples of 3 isequal to 810. Find the two numbers. |
|
Answer» |
|
| 2364. |
If x=a^(2) - bc, y=b^(2) - ca, z=c^(2) - ab then what is the value of (ax+by+ cz)/( (a+b+c) (x+y+z) ) |
|
Answer» |
|
| 2365. |
A cylinderical bucket. 32 cm high with radius of base 18 cm is filled with sand . This bucke tis empited on the ground and a coincal heap of sand is formed. If the heigh of the conical beap is 24 cm. Find the radius and slant height of the heap. |
|
Answer» |
|
| 2366. |
If diamond is called gold, gold is called silver, silver is called ruby and ruby is called emeraid, which is the cheapest jewel? |
|
Answer» Diamond |
|
| 2367. |
ABCD is a cyclic quadrilateral in which AB is parallel to DC and AB is a diameter of the circle. Givenangle BED = 65^(@), Calculate (i)angle DAB (ii)angle BDC |
|
Answer» |
|
| 2368. |
A right triangle, whose base and height are 15 cm and 20 cm. respectively is made to revolve about its hypotenuse. Find the volume and surface area of the doble cone so formed.(use pi = 3.14) |
|
Answer» Surface area of the doubled cone `=1318.8 cm^(2)` |
|
| 2369. |
Which of the following is/are correct ? |
|
Answer» `5 o+_(4) 3 -= 7 ox_(9) 8` (mod 5) (ii) SUBSTITUTE the values in theoptions in the given inequations. (III) The point which satisfies thegiven inequations is the required point. |
|
| 2371. |
Fill in the blanks using the correct word given in bracket : All square are ........... . |
|
Answer» |
|
| 2372. |
Two coins are tossed simultaneously. What is the probability of getting at leastone head? |
|
Answer» |
|
| 2373. |
A point P is reflected in the x - axis . Co - ordinates of its image are (8,-6). Find the co - ordinates of the image of P under reflection in the y - axis. |
|
Answer» |
|
| 2374. |
Find the zeroes of the polynomial x^(2)-3 and verify the relationship between the zeroes and the coefficients. |
|
Answer» |
|
| 2375. |
Mention the degrees of the polynomialsgiven : |
|
Answer» |
|
| 2376. |
Solve the following equations for (x - 3)^(2) and (y + 2)^(2) :2x^(2) + y^(2) - 12x + 4y + 16 = 0 and3x^(2) - 2y^(2) - 18x - 8y + 3 = 0. |
|
Answer» Solution :When it is said that solve for x and y then we have to find such values of x and y which satisfy both the equations. Similarly if we are asked that solve for `(x - 3)^(2)` and`(y - 2)^(2)`, then we have to find the value of `(x - 3)^(2)` and `(y + 2)^(2)` which satisfy the above two equations. First take the first equation as `2(x^(2) - 6x) + (y^(2) + 4y) = - 16` IMPLIES`2(x^(2)-6x+9) + (y^(2) + 4y + 4) = - 16 + 18 + 4` implies`2(x - 3)^(2) + (y + 2)^(2) = 6 ""....(1)` Now, take the second equation as `3(x^(2) - 6x) - 2 (y^(2) + 4y) = - 3` `implies 3(x^(2) - 6x + 9) - 2 (y^(2) + 4y + 4) = - 3 + 27 - 8` `implies 3(x - 3)^(2) - 2 (y-2)^(2) = 16"....(2)"` Let`(x - 3)^(2)` = u and `(y + 2)^(2) = v`. So, equations (1) and (2) become 2u + v = 6....(3) and3u - 2v = 16....(4) Multiplying equation (3) by 2, we get 4u + 2v = 12....(5) ADDING equations (5) and (4), we get 4u + 2v = 12 `(3u - 2v = 16 )/(7u = 28)` `thereforeu = 4 implies (x - 3)^(2) = 4` Putting u = 4 in equation (3), we get 2(4) + v = 6implies v = - 2implies`(y + 2)^(2) = - 2` But square of any real number cannot be negative. So, `(x - 3)^(2) = 4` and `(y + 2)^(2)` does not exist. |
|
| 2377. |
Solve : (a)/(ax-1)+(b)/(bx-1)=a+b, where a+b ne 0, ab ne 0. |
|
Answer» |
|
| 2378. |
A dealer sells goods/services, worth Rs 30,000 to some other dealer in the same town at a discount of 25%. If the rate of GST is 12%, find the amount of bill. |
|
Answer» |
|
| 2379. |
One root of the equation x^2 +ax +3=0 is 1.Find the value of a. |
| Answer» | |
| 2380. |
For which values of a and b are zeroes of q(X)=x^(3)+2x+a also zeroes of the polynomial p(x)=x^(5)-x^(4)-4x^(3)+3x^(2)+3x+b? Which zeroes of p(x) are not zeroes of p(x)? |
|
Answer» <P> `:. ""` q(x) p(x) is a factor of p(x). Now,`""` divide p(x) by q(x).  By factor THEOREM r(x)=0 `implies(-a-1)x^(2)+(3+3a)x+(b-2a)=0` `implies "" -a-1=0 "" and ""3+3a=0 "" and ""b-2a=0` `implies "" a=-1"" and ""a=-1 "" and ""b=2a` `implies "" a=-1 "" and ""b=-2""` Ans. Now,the other zeroes are given by `x^(2)-3x+2=0` `implies "" x^(2)-2x-x+2=0` `implies "" x(x-2)-1(x-2)=0` `implies "" (x-2)(x-1)=0` `implies "" x-2=0 "" or ""x-1=0` `implies "" x=2 "" or ""x=1 ""` Ans. |
|
| 2381. |
Will the median class and modal class of grouped data always by different? Justify your answer. |
| Answer» SOLUTION :Not, ALWAYS, It DEPENDS on the GIVEN DATA. | |
| 2382. |
There is a 7m high statue standing on a cliff. At a point P on the ground, the angle of elevation of the foot of the statue is alpha. After walking 34 metres towords the cliff from that point, the angle of elevation of the top ofthe statue is (90^(@)-alpha), find the height of the cliff if tanalpha=1/2. |
|
Answer» |
|
| 2383. |
The point P (5, 3) was reflected in the origin to get the image P'. Name the figure PMP'N. |
|
Answer» |
|
| 2384. |
Find the sum of first 51 terms of an AP whose second and third terms are 14 and 18 respectively. |
|
Answer» |
|
| 2385. |
Solve 2(y^2-6y)^2-8(y^2-6y+3) - 40 =0 |
|
Answer» |
|
| 2386. |
When the numerator of a fraction is increased by 4, the fraction increases by (2)/(3). What is the denominator of the fraction? |
|
Answer» |
|
| 2387. |
A ladder 10m long reaches a window 8m above the ground. Find the distance of foot of the ladder from base of the wall. |
|
Answer» |
|
| 2388. |
The volume of a solid cylinder is 96228 cm^(3)and the ratio of its radius to its height is 9:14. Find the total surface area of the cylinder. |
|
Answer» |
|
| 2389. |
At a point, the angle of elevation of a tower is such that its tangent is 5/12. On walking 240 m nearer to the tower, the tangent of the angle of elevation becomes 3/4. Find the height of the tower. |
|
Answer» |
|
| 2390. |
Find the distance between the following pairs of points : (-5, 7), (-1, 3) |
|
Answer» |
|
| 2391. |
A man wishes to determine the height of a tall building . In the middle of the horizontal field next to the buliding, there is a sign post whose top measures to be 2.5 m above the ground. The man then backup from the post away from the building until the top of the post just lines up with the top of the building and marks the spot where his feet are. the man then measures the distances shown in the adjoining figure. if the eyes of a man standing on the ground are 1.4 m a bove the ground, find the height of the building. |
|
Answer» |
|
| 2392. |
How many triangles are there in the figure given below ? |
|
Answer» 5 |
|
| 2393. |
A Sumof ₹ 3150is to be used to give six cash prizes to students of a school for overall academicperformance, punctuality, regularity. cleanliness, confidence and creativity. Ifeach prize is ₹ 50 lessthan its precedingprize, find the valueof each of the prizes.(a)Which valueaccording to you shouldbe awardedwiththe maximum amount ? Justifyyour answer.(b)Can you add more values to the above ones whichshould be awarded ? |
|
Answer» (b)Many more can be added like, HONESTY, GOOD habitsfriendship, respecting elders, LOVING youngers, . . . , etc |
|
| 2394. |
Find the seventh term from the end of the series : sqrt(2),2,2sqrt(2), . . . .. . . . ,32. |
|
Answer» |
|
| 2395. |
A container sphaded like a right circular cylinder having radius 6cm and height 15cm is full of ice-cream.The ice-creams is to be filled into cones of height 12 cm and diameter 6cm, having a hemispherical shape on the top. Find the number of such cones which can be filled with ice-cream. |
|
Answer» |
|
| 2396. |
Ineach of the following find the value of 'k', forwhich the points are collinear : (1) (7,-2), (5,1), (3,k) (2) (8,1), (k,-4), (2,-5) |
|
Answer» |
|
| 2398. |
One card is drawn from a well shuffled deck of cards . Calculate the probability that the card will . (i) be an ace (ii) not be an ace . |
|
Answer» |
|
| 2400. |
Draw a line segment of length 7 cm. Find a point P on it which divides it in the ratio 3:5. |
|
Answer» Solution :Steps of Construction : 1. DRAW a line segment AB = 7 cm. 2. Draw `AX"||"BY` such that `angleAand angleB` are acute angles. 3. Divide AX and BY in 3 and 5 parts equally by compass and mark `A_(1),A_(2),A_(3),B_(1),B_(2),B_(3),B_(4)and B_(5)` respectively. 4. Join `A_(3)B_(5)` which intersect AB at P and divides `AP: PB = 3:5.` Hence P is the REQUIRED point on AB which divide it in `3:5.` Verification (Justicicatio) : `In DeltaAA_(3)P and DeltaBB_(5)P` `""AX"||"BY""("by construction")` `""angleA=angleB""("alt.angles")` `""angleA_(3)PA=angleB_(5)PB""("vertically opp. angles")` `therefore""DeltaA A_(3)P~DeltaBB_(5)P""("by AA criterion of SIMILARITY")` `implies""(A A_(3))/(BB_(5))=(AP)/(BP)""("LET ecah equal part = c cm" thereforeA A_(1)=A_(1)A_(2)=B_(1)B_(2)...=x)` `implies""(3x)/(5x)=(AP)/(BP) implies""AP:BP=3:5` 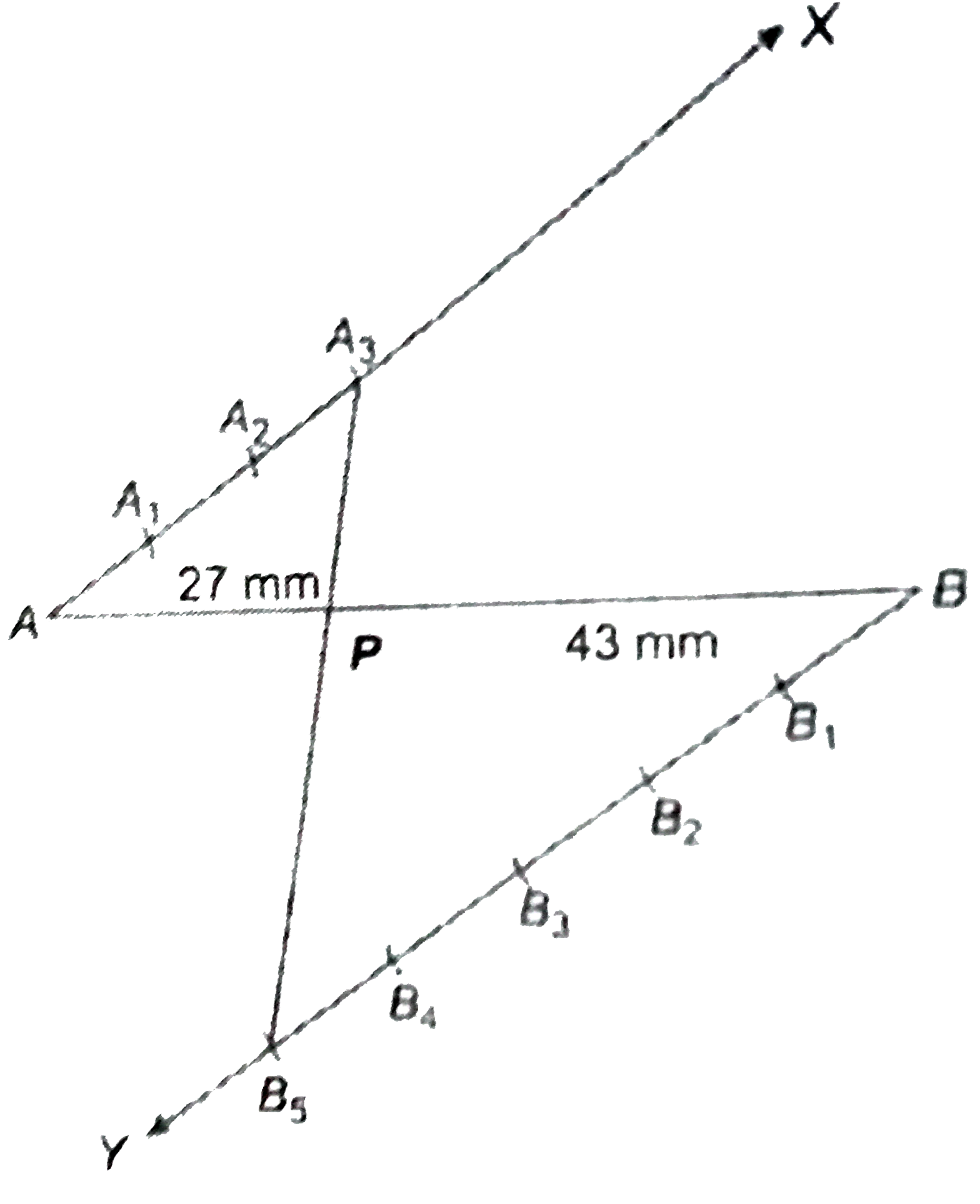
|
|