InterviewSolution
Saved Bookmarks
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2451. |
Use a graph paper for this question . (Take two divisions = 1 unit on both the axes.) Plot the points P (3,2) and Q(-3,-2) . From P and Q , draw perpendiculars PM and QN on the x - axis. Assign the special name to geometrical figure PMQN and find its area. |
|
Answer» |
|
| 2452. |
Given cot theta =(7)/(8) , then evaluate(i)((1+sin theta )( 1-sin theta ))/( (1+cos theta )(1-cos theta )) ""(ii)((1+sin theta ))/( cos theta ) |
|
Answer» (II) ` (8+sqrt (113))/( 7) ` |
|
| 2453. |
If x= 2 is a factor of x^2+ ax + b and a +b =1. find the values of a and b. |
|
Answer» |
|
| 2454. |
Which is the most suitable Venn diagram among the following ,Which represents interrelationship among Antisocial element,Pick pockets and black mailers? |
|
Answer»
|
|
| 2456. |
Find the mean, median and mode of the following data. |
|
Answer» |
|
| 2457. |
Digonals of a trapezium ABCD with AB||DC intersect each other at the point O. If AB= 2 CD, find the ratio of the areas of triangles AOB and COD. |
|
Answer» |
|
| 2458. |
Fill in the blanks,(a) Number of terms in expansion (-2x + 3y)^17is _______. |
|
Answer» |
|
| 2459. |
A dice is rolled two times or two dice are rolled together. Find the probability of getting: an even number on each dice. |
|
Answer» |
|
| 2460. |
Find the values of constants a and b when x- 2 and x + 3 both are the factors of expression x^3+ax^2+bx -12. |
|
Answer» |
|
| 2461. |
5 Pencils and 7 Pens together cost Rs 50, 7 Pencils and 5 Pens togethercost Rs 46. Find the cost of one Pencil and that of one Pen. |
|
Answer» |
|
| 2462. |
On a rainyday , a shopkeeper sells two colours ( black and red ) of umbrellas. He sells not more than 20 umbrellas of each colour. At least twice as many black ones are sold as the red one. If the profit on each of the black umbrellas is Rs. 30 and that of the red ones is Rs. 40 , then how many of each kind must be sold to get a maximum profit ? |
|
Answer» 20,10 `x ge 0 and x le 20` ` y ge 0 and y le 20`. `x ge 2y`. Profit function p=30x+40y The maximum profit attains at C(20,10). The maximum profit =`30xx20+40xx10=600+400=Rs. 1000`. Number of black umbrella =20. Number of red umbrellas =10 
|
|
| 2463. |
There is a circular path around a sports field. Sonia takes 18 minutes to derive one round of the field, while Ravi takes 12 minutes for the same. Suppose they both start at the same point and at the same time, and go in the same direction. After how many minutes will they meet again at the starting point? |
|
Answer» |
|
| 2464. |
If the 3rd and the 9th terms of an AP are 4 and -8 respectively, which term of this AP is zero? |
|
Answer» |
|
| 2465. |
A fruit seller has certain number of oranges. He divides them into two lots A and B. He sells the lot at 3 oranges for Rs. 2 and the lot B at 1 oranges for Rs. 1. Thus he gets Rs. 400, if he had sold the first lot at 1 oranges for Rs. 1 and the second lot B at 5 oranges for Rs. 4, he would have got Rs. 460. Find the total number of oranges. |
Answer» SOLUTION :First of all we make a rough sketch. Let the number of oranges in lot A and B are X and y respectively. 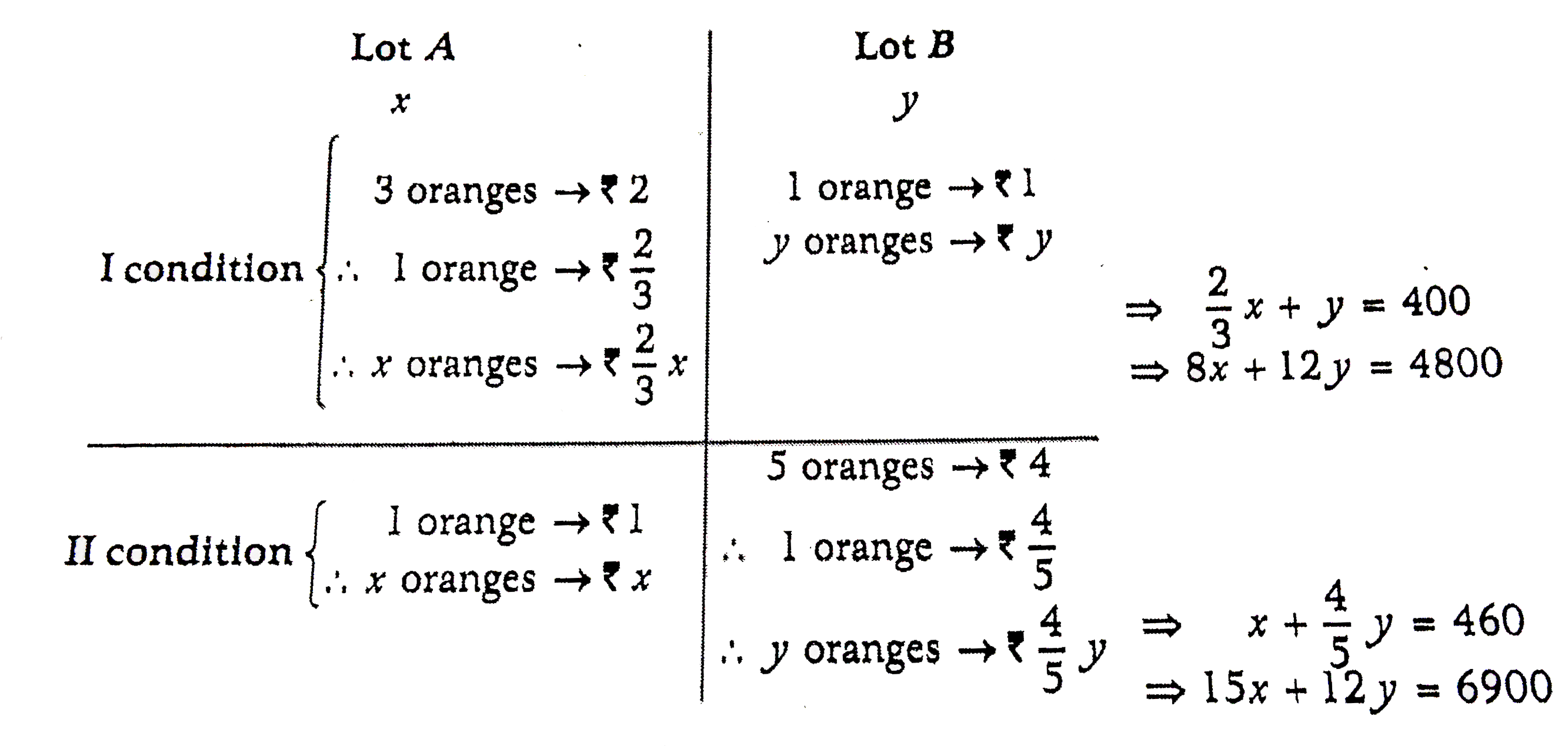 SUBTRACTING equation (1) from (2), we get Subtracting equation (1) from (2), we get 7x = 2100 implies x = 300 Putting x = 300 in equation (1), we get `(2)/(3) (300) + y = 400 impliesy = 200` `therefore`Total number of oranges= x + y = 300 + 200 = 500 |
|
| 2466. |
Which of the following point is equidistant from (3, 2) and (-5,-2) ? |
|
Answer» `(0,2)` |
|
| 2467. |
(2 tan30 ^@) /( 1- tan ^ 230 ^@ ) |
|
Answer» `cos 60^(@) ` |
|
| 2468. |
Find the common difference and 99th term of the arithmetic progression : 7 3/4, 9 1/2, 11 1/4,………. |
|
Answer» |
|
| 2469. |
The point P (5, 3) was reflected in the origin to get the image P'. Find the area of the figure PMP'N. |
|
Answer» |
|
| 2470. |
Construct a triangle similar to a given DeltaABC with its sides 2/5 of the corresponding sides of Delta ABC, firstly a ray BX is drawn such that CBX is an acute angle and X lies on the opposite side of A with respect to BC then points B_1, B_2, B_3. are located on BX at equal distances Which two points will be joined in the next step. |
|
Answer» |
|
| 2471. |
A sum of Rs54,000 is invested partly in shares paying 6% dividend at 40% premium and partly in 5% shares at 25% premium. If the nominal value of one share in each company is Rs100 and the total income of the man is Rs 2,240, find the money invested in the second company. |
|
Answer» |
|
| 2472. |
A circle is touching the side BC of a triangleABC at point P and touching AB and AC produced at Q and R respectively. Prove that AQ=(1)/(2)("perimeter of "triangle ABC). |
Answer» SOLUTION :Given : triangle ABC and a circle which touches BC, AB and AC in P,Q and R respectively. Proof : Since the length of the two tangents DRAWN from an external point to a circle are equal THEREFORE,  `AQ=AR""...(1)` `BQ=BP""...(2)` and `""CP=CR""...(3)` Now, PERIMETER of `triangle`ABC=AB+BC+AC `=AB+BP+PC+AC` `=AB+BQ+CR+AC""`[from (2) and (3)] `=AQ+AR=2AQ""`[from (1)] `:.""`Perimeter of `triangleABC=2AQ` `implies""AQ=(1)/(2)xx`(perimeter of `triangleABC`) HenceProved. |
|
| 2474. |
Two customers shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday) . Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on (i) the same day ? (ii) consecutive day ? (iii) different days ? |
|
Answer» (II) `8/25` (III) `4/5` |
|
| 2475. |
Find the 8^(th) term of the sequence : (3)/(4),1(1)/(2),3,. . . . . . . . . . . |
|
Answer» |
|
| 2476. |
If 2[{:(,3,x),(,0,1):}]+3[{:(,1,3),(,y,2):}]=[{:(,z,-7),(,15,8):}], find the values of x, y and z. |
|
Answer» |
|
| 2478. |
Find the area of the shaded region in the given circle of radius 7 cm and sector angle is 30^(@) as in the figure. |
|
Answer» |
|
| 2479. |
Paula jogged for a total of 30 minutes. Her average speed for the first 10 minutes was 5 miles per hour. During the remainder of her time, she jogged 2.5 miles. What was Paula's average for her entire jog ? |
|
Answer» `6(1)/(2)` mph `(5)/(6)+(5)/(2)=(5)/(6)+(15)/(6)=(20)/(6)` So Paula jogged a total of `(20)/(6)("or " 3(1)/(3))` miles. Now divide this distance by the time. `((20)/(6))/((1)/(2))=(20)/(6)xx2=(40)/(6)` So Paula jogged at an overall average rate of `(40)/(6)`, or `6(2)/(3)`, miles per hour. |
|
| 2480. |
A right triangle, whose base and height are 15 cm and 20 cmrespectively is made to revolve about its hypotenuse. Find the volume and surface area of the double cone so formed. |
|
Answer» |
|
| 2481. |
A die is thrown once. What is the probability of getting an even number? |
|
Answer» |
|
| 2482. |
BL and CM are medians of a triangle ABC right angled at A. Prove that 4(BL^(2)+ CM^(2))=5BC^(2) |
|
Answer» |
|
| 2483. |
If point P(9a-2, b) divides the line segment joining the points A(3a+1, -3) and B(8a, 5) in the ratio 3 : 1, then find the values of a and b. |
Answer» SOLUTION :`therefore""9a-2=(3(8a)+1(3a+1))/(3+1)`  `rArr""36a-8=24a+3a+1` `rArr""9a=9""rArr""a=1` `and""-B=(3(5)+1(-3))/(3+1)=3` `rArr""b=-3` |
|
| 2485. |
What number should be added to 2x^3 - 3x^2 - 8x + 3 so that the resulting polynomial leaves the remainder 10 when divided by 2x + 1 ? |
|
Answer» |
|
| 2486. |
Draw the graphs of the following equations :2x-y=1, x+2y=13Find the solution of the equations from the graph and shade the triangular region formed by the lines and the Y - axis. |
|
Answer» |
|
| 2487. |
O is any point inside a rectangle ABCD (see the given figure). Prove that OB^(2)+OD^(2)= OA^(2)+OC^(2). |
|
Answer» |
|
| 2488. |
The marks scored by 30 students of class X of a certain school in a Mathematics paper consisting of 100 marks are presented in table below. Find the mean of the marks obtained by the students. |
|
Answer» |
|
| 2489. |
Find the zeroes of the quadratic polynomial x^(2)+7x+10, and verify the relationship between the zeroes and the coefficients. |
|
Answer» |
|
| 2490. |
If the roots of a quadratic equation ax^(2) + bx + c = 0 are real and equal then b^(2) =… |
| Answer» ANSWER :B | |
| 2491. |
Three identical coins are tossed together. What is the probability of obtaining : exactly two heads ? |
|
Answer» |
|
| 2492. |
The perimeter of a rectangularplot is 32m.If theincreased by 2 m and thebreadth is decreased by 1 m,the area of the plotremainsthe same.Find the length and breadth fo the plot . |
|
Answer» |
|
| 2493. |
If (a)/( b+c) = x, (b)/ (c+a) = y, (c)/( a+b) = z, whta is the value of (1)/( 1+x) + (2)/( 1+y) + (1)/( 1+z)? |
|
Answer» |
|
| 2495. |
Find the zeroes of the quadratic polynomial x^(2)-3 and verify the relationship between the zeroes and coefficients. |
|
Answer» |
|
| 2496. |
Two dice are thrown simultaneously. Find the probability that : the total (sum) of the numbers on the dice is 9. |
|
Answer» |
|
| 2497. |
Given P = {x: 5 lt 2x - 1 le 11, x in R }and Q = {x : -1 le 3 +4x lt 23, x in I}where R = {real number } and I = { integers}. |
|
Answer» |
|
| 2498. |
What is the area of the triangle formed by the points (a,c+a),(a^(2),c^(2)) and (-a,c-a) ? |
| Answer» ANSWER :D | |
| 2499. |
Solve the following pair of linear equations by the substitution method. (3x)/(2)-(5y)/(3)=-2 (x)/(3)+(y)/(2)=(13)/(6). |
|
Answer» |
|
| 2500. |
Write of the following are Aps? IF they form an AP, find the common difference d and write three more terms. (i)2,4,8,16...... (ii) 2,5/2,3,7/2... (iii) -1.2,-3.2,-5.2,-7.2.... (iv)-10,-6,-2,2.... (v) 3,3+sqrt2,3+2sqrt2,3+3sqrt2.... (vi)0.2,0.22,0.222,0.2222... (vii) 0,-4,-8,-12... (viii) -1/2,-1/2,-1/2,-1/2.... (ix)1,3,9,27... (x) a,2a,3a,4a (x i) a,a^2,a^3,a^4..... (x ii)sqrt2,sqrt8,sqrt18,sqrt32.... (x iii) sqrt3,sqrt6,sqrt9,sqrt12... (x iv) 1^2,3^2,5^2,7^2,... (xv)=1^2,5^2,7^2,73,.... |
|
Answer» |
|