InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3001. |
One card is drawn from a well - shuffled deck of cards . Find the probability of getting a face card . |
|
Answer» |
|
| 3002. |
The simpliest value of (sqrt5 (sqrt(3 - sqrt5)))/(sqrt2 + sqrt(7 - 3 sqrt5)) is |
|
Answer» 1 |
|
| 3003. |
If tan (A + B) = sqrt(3) and tan (A- B) = 1/(sqrt3) , 0^@ < A + B le 90^@, A > B, then find the value of A and B. |
|
Answer» |
|
| 3004. |
A company provided Z-security services for the taxable value of 64,500. Rate of GST is 18%. Company has padi GST of 1550 for laundry services and uniform etc. What is the amount of ITC (input Tax Credit)? Find the amount of CGST and SGST payable by the company. |
|
Answer» |
|
| 3005. |
Find the coordinates of a point A, where AB is the diameter of a circle whose centre is (2, - 3) and B is (1, 4). |
|
Answer» |
|
| 3006. |
If the third and the 9th terms of an A.P. be 4 and -8 respectively, find which term is zero ? |
|
Answer» |
|
| 3007. |
If A(-14,-10) , B (6,-2) is given . Find the coordinates of points which divide segment AB into fourequal points . |
|
Answer» |
|
| 3008. |
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the anglebetween which is 60^(@). Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents. |
|
Answer» Solution :In order to draw the PAIR of TANGENTS, we follow the following steps. Steps of construction 1. Takea POINT O on the plane of the paper and draw a circle of radius OA=4 cm. 2. Produce OA to B such that OA=AB=4 cm. 3. Taking A as the centre draw a circle of radius AO=AB=4 cm. Suppose it CUTS the circle drawn in step 1 at P and Q. 4. Join BP and BQ to get desired tangents. Justification In `DeltaOAP`, we have OA=OP=4cm (`:.` Radius ) ALSO, AP=4cm (`:.` Radius of circle with centre A ) `:. DeltaOAP` is equilateral `implies anglePAO=60^(@)` `implies angleBAP=120^(@)`  In `DeltaBAP`, we have `BA=AP " and " angleBAP=120^(@)` `: angleABP= angleAPB =30^(@)` `implies anglePBQ=60^(@)` Alternate method Steps of construction 1. Take a point O on the plane of the paper and draw a circle with centre O and radius OA=4 cm. 2. At O construct radii OA and OB such that to `angleAOB` equal `120^(@)` i.e., supplement of the angle between the tangents. 3. Draw perpendicular to OA and OB at A and B, respectively. Suppose these perpendicular intersect at P. Then, PA and PB are required tangents. 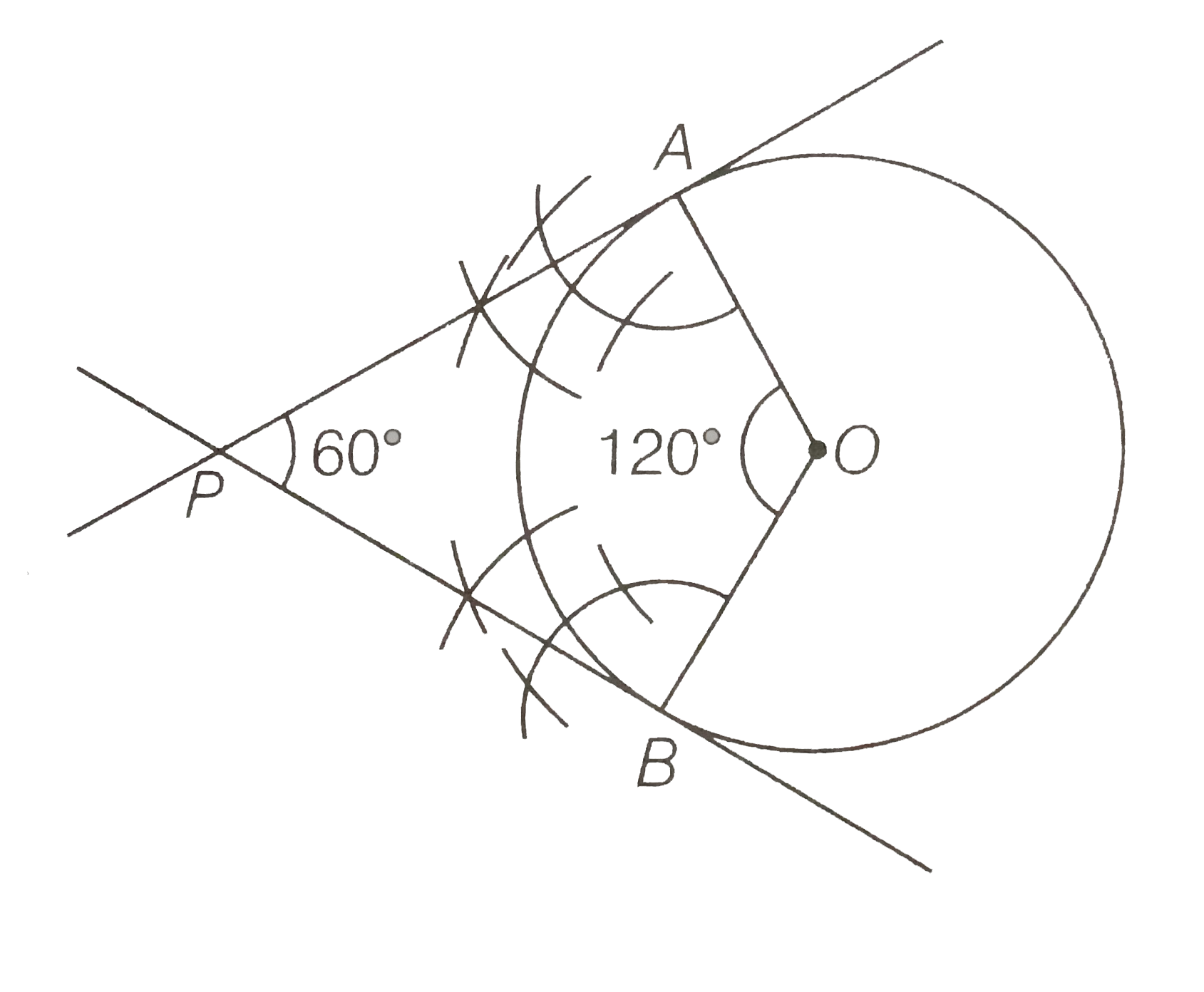 Justification In quadrilateral OAPB, we have `angleOAP=angleOBP=90^(@)` and `angle AOB=120^(@)` `:. angleOAP+angleOBP+angleAOB+angleAPB=360^(@)` `implies 90^(@)+90^(@)+120^(@)+angleAPB=360^(@)` `:. angleAPB=360^(@)-(90^(@)+90^(@)+120^(@))` `=360^(@)-300^(@)=60^(@)` |
|
| 3009. |
Find the next two terms of the series : 2-6+18-54 . . . . . . . . . . . . . |
|
Answer» |
|
| 3010. |
Find the roots of an equation by factorisation(2x-3)=sqrt(2x^(2)-2x+21) |
|
Answer» |
|
| 3011. |
Construct a less than ogive and a more than ogive from the following data : |
Answer» SOLUTION :Cumulative frequency DISTRIBUTION table according to AGES ( in YEARS) less than and more than are : 
|
|
| 3012. |
squareABCD is a rectangle. Triangle EFB has an area of 2 cm ^(2) . triangleBEC has an area of 3cm^(2). Find the area of shaded region. |
|
Answer» |
|
| 3013. |
P and Q have co-ordinates (-2, 3) and (5, 4) respectively. Reflect P in the x-axis to P' and Q in the y-axis to Q'. State the co-ordinates of P' and 'Q . |
|
Answer» <P> |
|
| 3014. |
Which point lies on the perpendicular bisector of the line segment joining the points A (-3, 4) andB (3,-4)? |
|
Answer» |
|
| 3015. |
Find the co-ordinates of the points which divide the line segment joining A (-2, 2) and B(2, 8) into four equal parts. |
|
Answer» Solution :Let P, Q and R be the poins on line segment AB such that `""AP=PQ=QR=RB` Let `""AP=PQ=QR=RB=k`  Now, `(AP)/(PB)=(k)/(3k)=(1)/(3)` Therefore, P divides AB internally in the ration 1 : 3. `because" Internally RATIO"=((m_(1)x_(2)+m_(2)x_(1))/(m_(1)+m_(2)), (m_(1)y_(2)+m_(2)y_(1))/(m_(1)+m_(2)))` `""P=((1xx2+3(-2))/(1+3), (1xx8+3xx2)/(1+3))=((2-6)/(4), (8+6)/(4))=((-4)/(4), (14)/(4))=(-1, (7)/(2))` Again, `""(AR)/(RB)=(3k)/(k)=(3)/(1)` Therefore, R divides AB internally in the ratio 3 : 1. `therefore""R=((3xx2+1xx(-2))/(3+1), (3xx8+1xx2)/(3+1))` `""=((6-2)/(4), (24+2)/(4))=((4)/(4), (26)/(4))=(1, (13)/(2))` Also, `""(AQ)/(QB)=(2k)/(2k)=(1)/(1)` `therefore` Q is the mid-point of AB. `therefore""Q=((-2+2)/(2), (2+8)/(2))[because "mid-point"=((x_(1)+x_(2))/(2), (y_(1)+y_(2))/(2))]` `i.e., ""Q=((0)/(2), (10)/(2))=(0, 5)` So, required POINTS are `(-1, (7)/(2)), (0, 5) and (1, (13)/(2))`. |
|
| 3016. |
A cylindrical container with diameter of base 42 cm contains sufficient water to submerge a rectangular solid of iron with dimensions 22 cm xx 14 cm xx 10.5 cm. Find the rise in level of the water when the solid is submerged. |
|
Answer» |
|
| 3017. |
Find the volume of a cone whose slant height is 17 cm and radius of base is 8 cm. |
|
Answer» |
|
| 3018. |
Solve :x+y+z=5: 2x-y+z=9: x-2y+3z+16. |
|
Answer» |
|
| 3019. |
Using properties of proportion solve for x, given (sqrt(5x)+sqrt(2x-6))/(sqrt(5x)-sqrt(2x-6))=4. |
|
Answer» |
|
| 3020. |
Statements: 1. Most teachers are boys. 2. Some boys are students. Conclusions: 1. Some students are boys. 2. Some teachers are students. |
|
Answer» If only conclusion I follows, `Simplies ` Students ` Timplies ` teachers 
|
|
| 3021. |
In the given figure, their are three semi circular arcs and one circle. The smaller arcs are equal. If AB = 6 cm, AC = 4 cm. Find the complete length of two figure. ltrbgt |
|
Answer» |
|
| 3022. |
Three identical coins are tossed together. What is the probability of obtaining : all tails ? |
|
Answer» |
|
| 3025. |
Find the blankusing the correct word given in bracket : All squares are ................(similar, Congruent) |
|
Answer» |
|
| 3026. |
In the following data, find the values of p and q. Also find the median class and modal class. |
|
Answer» |
|
| 3027. |
What is Sachin's rank from the top in a class of 25 students? I. Sachin ranks three ranks above Amit who ranks 18^(th) from the bottom. II. Sachin's rank from the top is two ranks below Deepti who ranks 23^(rd) from the bottom. |
|
Answer» the data in statement I alone are sufficient to answer the question, while the data in statement II alone are not sufficient to answer the question, From II, Deepti ranks `23^(rd)` from the bottom and hence, `3^(rd)` from the top. Sachin, being 2 ranks below Deepti, is, THUS, `5^(th)` from the top. |
|
| 3029. |
Prove thatsqrt ((1-cos theta )/( 1+cos theta ) ) = cosec theta -cot theta , 0le theta le 90 ^(@) |
|
Answer» |
|
| 3030. |
Find the mean, median and mode of the following data : |
|
Answer» |
|
| 3031. |
The radii of the internal and external surfaces of a metallic spherical shell are 3 cm and 5 cm respectively. It is melted and recast into a solid right circular cone of height 32 cm. Find the diameter of the base of the cone. |
|
Answer» |
|
| 3032. |
Pickthe constantpolynomials. Find the zeros of thispolynomials ? |
|
Answer» No xeros forthis polynomial a(x) |
|
| 3033. |
Find the roots of the quadratic equation 3x^2 - 2sqrt(6)x + 2 = 0. |
|
Answer» |
|
| 3034. |
Write the following expressions as log N and find their values. log_(2)16 - log_(2) 2 |
|
Answer» |
|
| 3035. |
A man travels a distance of 196 km by train and returns in a car which travels at a speed of 21 km/hours more than the train if the total journey takes 11 hour. Find the average speed of the train and the car respectively. |
|
Answer» |
|
| 3036. |
Areas of two similar triangle are in the ratio of 5:3, then the ratio of their corresponding sides is : |
|
Answer» `5:3` |
|
| 3037. |
The upper part of a tree, broken by the wind makes an angle of 60° with the ground and the distance from the roots to the point where the top of the tree meets the ground is 20 m. The length of the broken part of the tree is |
|
Answer» 20 m |
|
| 3039. |
Write value of "^(2n-1)C_(5)+"^(2n-1)C_(6)+"^(2n)C_(7) use ["^(n)c_(r)+^(n)C_(r-1)="^(n+1)C_(r)] |
|
Answer» |
|
| 3040. |
Find which one word cannot be made from the letters of the given word. TEACHERS |
|
Answer» REACH |
|
| 3041. |
Using ruler and compasses only, Inscribe a circle in the A ABC of each side equal to 6cm |
| Answer» | |
| 3042. |
When a metal cube is completely submerged in water contained in a cylindrical vessel with diameter 30 cm, the level of water rises by 1 (41)/(99) cm. Find :(i) the length of edge of the cube. (ii) the total surface area of the cube. |
|
Answer» |
|
| 3043. |
A hollow sphere of internal and external diameters 4 cm and 8 cm respectively is melted into a cone of base diameter 8 cm. Find the height of the cone. |
|
Answer» |
|
| 3044. |
Which is the better investment 16% 100rs shares at 80 or 20% 100rs shares at 120 ? |
|
Answer» |
|
| 3045. |
Check whether the givensequences form a G.P. or not: 8 , 24 , 72 , 216, . . . . . . . . . |
|
Answer» |
|
| 3046. |
Traveller : Jourey :: Sailor : ? |
|
Answer» Water |
|
| 3047. |
If A=[{:(,a,0),(,0,2):}], B=[{:(,0,-b),(,1,0):}], M=[{:(,1,-1),(,1,1):}] and BA=M^2, find the values of a and b. |
|
Answer» |
|
| 3048. |
Six friends went on a vacation to a hill station. They are to be accommodated in a row of nine cottages, each to a cottage. Mohan, Tanya and Roma do not want to live in a cottage at the end of a row. Babu and Mohan must not have anybody adjacent to their cottages. There is only an empty cottage between Mohan and Roma. Chander is adjacent to both Jayanthi and Roma Tanya is next to the cottage at the beginning. What is the maximum number of consecutive cottages that are occupied? |
|
Answer» 2 Six friends have to occupy 6 out of 9 cottages using the conditions (i) MT and R do not want to live in a cottage at the END of the ROW  (ii) B and M must not have anybody adjacent to their cottages. -B-and-M (iii) There is one empty cottage between M and R (if the cottage is empty, then nobody occupies it) M-R or R-M. (iv) C is adjacent to both J and R JCR or RCJ (v) T is NEXT to the cottage at the beginning.  Looking into these information, the final arrangement will be:  Maximum four consecutive cottages are occupied. |
|
| 3049. |
Six friends went on a vacation to a hill station. They are to be accommodated in a row of nine cottages, each to a cottage. Mohan, Tanya and Roma do not want to live in a cottage at the end of a row. Babu and Mohan must not have anybody adjacent to their cottages. There is only an empty cottage between Mohan and Roma. Chander is adjacent to both Jayanthi and Roma Tanya is next to the cottage at the beginning. Who is in the third cottage? |
|
Answer» Jayanthi Six friends have to occupy 6 out of 9 cottages using the conditions (i) MT and R do not want to live in a cottage at the END of the row  (ii) B and M must not have anybody adjacent to their cottages. -B-and-M (iii) There is one empty cottage between M and R (if the cottage is empty, then nobody OCCUPIES it) M-R or R-M. (iv) C is adjacent to both J and R JCR or RCJ (v) T is next to the cottage at the beginning.  Looking into these information, the final arrangement will be:  Jayanthi is in the third cottage. |
|
| 3050. |
Six friends went on a vacation to a hill station. They are to be accommodated in a row of nine cottages, each to a cottage. Mohan, Tanya and Roma do not want to live in a cottage at the end of a row. Babu and Mohan must not have anybody adjacent to their cottages. There is only an empty cottage between Mohan and Roma. Chander is adjacent to both Jayanthi and Roma Tanya is next to the cottage at the beginning. Which cottages are empty? |
|
Answer» 1,6,8 Six friends have to occupy 6 out of 9 cottages using the conditions (i) MT and R do not want to live in a cottage at the end of the row  (II) B and M must not have anybody adjacent to their cottages. -B-and-M (iii) There is one empty cottage between M and R (if the cottage is empty, then NOBODY occupies it) M-R or R-M. (iv) C is adjacent to both J and R JCR or RCJ (v) T is next to the cottage at the beginning.  Looking into these information, the FINAL arrangement will be:  The first, sixth and eighth cottages are empty. |
|