InterviewSolution
Saved Bookmarks
| 1. |
Draw a circle of radius 4 cm. Construct a pair of tangents to it, the anglebetween which is 60^(@). Also justify the construction. Measure the distance between the centre of the circle and the point of intersection of tangents. |
|
Answer» Solution :In order to draw the PAIR of TANGENTS, we follow the following steps. Steps of construction 1. Takea POINT O on the plane of the paper and draw a circle of radius OA=4 cm. 2. Produce OA to B such that OA=AB=4 cm. 3. Taking A as the centre draw a circle of radius AO=AB=4 cm. Suppose it CUTS the circle drawn in step 1 at P and Q. 4. Join BP and BQ to get desired tangents. Justification In `DeltaOAP`, we have OA=OP=4cm (`:.` Radius ) ALSO, AP=4cm (`:.` Radius of circle with centre A ) `:. DeltaOAP` is equilateral `implies anglePAO=60^(@)` `implies angleBAP=120^(@)`  In `DeltaBAP`, we have `BA=AP " and " angleBAP=120^(@)` `: angleABP= angleAPB =30^(@)` `implies anglePBQ=60^(@)` Alternate method Steps of construction 1. Take a point O on the plane of the paper and draw a circle with centre O and radius OA=4 cm. 2. At O construct radii OA and OB such that to `angleAOB` equal `120^(@)` i.e., supplement of the angle between the tangents. 3. Draw perpendicular to OA and OB at A and B, respectively. Suppose these perpendicular intersect at P. Then, PA and PB are required tangents. 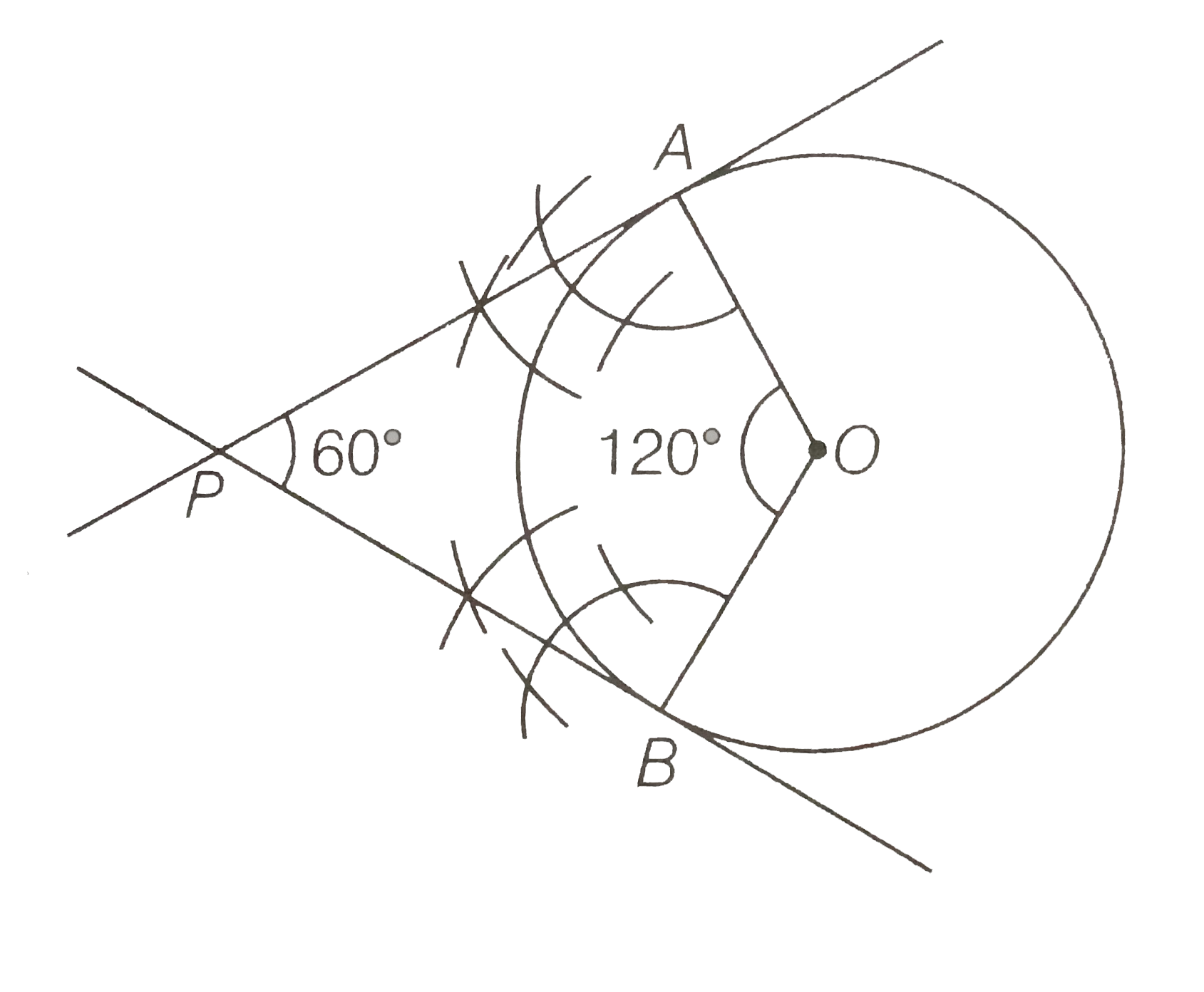 Justification In quadrilateral OAPB, we have `angleOAP=angleOBP=90^(@)` and `angle AOB=120^(@)` `:. angleOAP+angleOBP+angleAOB+angleAPB=360^(@)` `implies 90^(@)+90^(@)+120^(@)+angleAPB=360^(@)` `:. angleAPB=360^(@)-(90^(@)+90^(@)+120^(@))` `=360^(@)-300^(@)=60^(@)` |
|