Explore topic-wise InterviewSolutions in .

This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.

3451.

Mr. Shameem invested 33.(1)/(3)% of his savings in 20% 50rs shares quoted at 60rs and the remainder of the savings in 10% 100rs shares quoted at 110rs. If his total income from these investments is 9200rs find (i) his total savings (ii) the number of 50rsshares the number of 100rs shares

Answer»


ANSWER :`(i) 79200rs` `(II) 440` `(III) 480`
Discussion
3452.

State whether the followmg sets are finite or infinite. (i) The set of months in a year. (ii) {1,2,3, ..., 99, 100) (iii) The set of prior numbers smaller than 99. (iv) The set of letters in the English alphabet. (v) The set of lines that can be drawn are parallel to the X-Axis (vi) The set of numbers which are muitiplies of 5. (vii) The set of circles passing through the origin (0,0).

Answer»


ANSWER :(i) FINITE (II) Finite (III) Finite
Discussion
3453.

How much should a man invest in 50rs shares selling at 60rs to obtain an income of 450rs if the rate of dividend declared is 10%. Also find his yield percent to the nearest whole number.

Answer»


ANSWER :`5400rs and `8%`
Discussion
3454.

The radius of the ends of a bucket of height 24 cm are 15 cm and 5 cm. Find its capacity .Also find the surface area of the buket .

Answer»


ANSWER :8171.43`CM^(3),1712.86 cm^(2)`
Discussion
3455.

Find the area of the quadrilateral whose vertices are A (0, 0), B (6, 0), C (4, 3) and D (0, 3).

Answer»


ANSWER :15 SQ UNITS
Discussion
3456.

In the following data, find thevalues of a and b . Find the median class modal class :

Answer»


ANSWER :a=14,b=43 MEDINA CLASS =150-200, MODAL class =150-200
Discussion
3457.

The marked price of an article is Rs. 6,000. A wholesaler sells it to a dealer at 20% discount. The dealer further sells the article to a customer at a discount of 10% on the marked price. If the rate of GST at each stage is 18%, find the amount of tax (under GST) paid by the dealer to the government.

Answer»


ANSWER :RS. 108
Discussion
3458.

An ink container of cylindrical shape is filled with ink upto 91% Ballpen refills of length 12 cm and inner diameter 2 mm are filled upto 84%. IF the height and radius of the ink container are 14 cm and 6 cm respectively, find the number of refills that can be filled with this ink.

Answer»


ANSWER :4550
Discussion
3459.

Find the volume and surface area of a sphere of radius 2.1 cm (pi = (22)/(7))

Answer»


ANSWER :`38.808 cm^3`
Discussion
3460.

By purchasing 25rs shares for 40rs each, a man gets 4 percent profit on his investments. What are rate percent is the company paying ? What is his dividend if he buys 60 shares ?

Answer»


ANSWER :`6.4% ; 96RS`
Discussion
3461.

(i) Solve 8x - 3y = 5xy and 6x - 5y = - 2xy. How many solutions, this system of equations has?(ii) Solve for x and y, by reducing the following equations in a pair of linear equations : 2x + 3y = 5xyand 3x - 2y = xy.

Answer»

Solution :(i) Given equations are8x - 3y = 5xy
and6x - 5y= -2xy
The given equations are not linear in the variable x and y. These can be REDUCED into linear equations.
If we put x = 0 in either of the equations, we get y = 0. Hence, x = 0 and y = 0 is a solution of these equations.
To find other solution, dividing each of th given equations by xy.
So,`(8)/(y) - (3)/(x) = 5`.... (1)
and`(6)/(y) - (5)/(x) = -2`....(2)
Let `(1)/(y)` = a and `(1)/(x)` = b then from equations (1) and (2), we get
`{:(8a - 3b = 5),(6A - 5b =-2):}}"linear equations"{:(....(3)),(....(4)):}`
Multiplying equation (3) by 5 and (4) by 3, we get
40a - 15b = 25....(5)
18a - 15b = - 6....(6)
Subtracting equation (6) from (5), we get
22a = 31
implies`a = (31)/(22)`
Putting `a = (31)/(22)` in equation (3), we get
`8 xx (31)/(22) - 3b = 5`
`(124)/(11) - 3b = 5implies-3b = 5 - (124)/(11)`
implies`-3b = - (69)/(11) implies b = (23)/(11)`
Now,`(1)/(y) = a implies(1)/(y) = (31)/(22)impliesy = (22)/(31)`
and `(1)/(x) = b implies(1)/(x) = (23)/(11)impliesx = (11)/(23)`
Hence, the solution of the given two equations are `{:(x = 0),(y = 0):}}` and `{:(x = (11)/(23)),(y = (22)/(31)):}}`.
So, the given system of equations has two solutions.
(ii) We have,
2x + 3y = 5xy.... (1)
3x - 2Y = xy.... (2)
Dividing equations (1) and (2) by xy, we get
`(2x)/(xy) + (3y)/(xy) = (5xy)/(xy) implies (2)/(y) + (3)/(x) = 5 ""...(3)`
and`(3x)/(xy) - (2y)/(xy) = (xy)/(xy) implies (3)/(y) - (2)/(x) = 1""....(4)`
Let`(1)/(x) = u` and `(1)/(y) = v`.
`therefore` Equations (3) and (4) become,
2v + 3u = 5....(5)
3v - 2u = 1 ....(6)
Now this is a PAIR of linear equations,multiplying equation (5) by 2 and equation (6) by 3, we get
4v + 6u = 10....(7)
9v - 6u = 3 ....(8)
On adding equations (7) and (8), we get
13v = 13impliesv = 1
Putting v = 1 in equation (5), we get
2(1) + 3u = 5implies3u = 3 implies u = 1
Now, u = 1 implies`(1)/(x) = 1` implies x = 1
and v = 1 implies `(1)/(y) = 1` implies y = 1
Hence, required solution is `{:(x = 1),(y = 1):}}`.
Discussion
3462.

Village K is towards which direction of the village N? I. Village M is to the north of village N and to the east of village K. II. Village D is to the west of village N and to the south of village K.

Answer»

if the data in statement I alone are sufficient to answer the QUESTION, while the data in statement II alone are not sufficient to answer the question,
if the data in statement II alone are sufficient to answer the question, while the data in statement I alone are not sufficient to answer the question,
if the data either in statement I alone or in statement II alone are sufficient to answer the question,
if the data given in both statements I and II together are not sufficient to answer the question,

Solution :Arrangement from I

Arrangement from II

Clearly, in each arrangement, K is to the north-west of N.
Discussion
3463.

The shadow of a tower at a time is three times as long as its shadow when the angle of elevation of the Sun is 60^(@). Find the angle of elevation of the Sum at the time of the longer shadow.

Answer»

`60^0`
`30^0`
`45^0`
`15^0`

Solution :Let AB = h be the height of a tower.
Let at Sun's elevation of `60^(@)`, its shadow be x.
some Applications of Trigonometry
Let `theta` be the ANGLE of elevation when its shadow is 3 times the FORMER i.e.,3x.
``In right `DeltaABC`,
`tan60^(@)=h/xrArrsqrt3=h/xrArrh=xsqrt3...(1)`
In right `DeltaABD`,
`tantheta=h/(3x)`
`=(xsqrt3)/(3x)"[from (1)]"`
`=1/sqrt3=tan 30^(@)`
`theta30^(@)`
Discussion
3464.

Draw a circle of radius 3cm. Draw a tangent to the circle making an angle of 30^(@) with a line passing through the centre.

Answer»

Solution :Draw a circle with centre `O` and radius `3cm` . Draw a radius `OA` and PRODUCE it to `B`. Make `/_AOP=60^(@)`. Draw `PQbotOP`, meeting `OB` at `Q`.
Then, `PQ` is the DESIRED TANGENT such that `/_OQP=30^(@)`.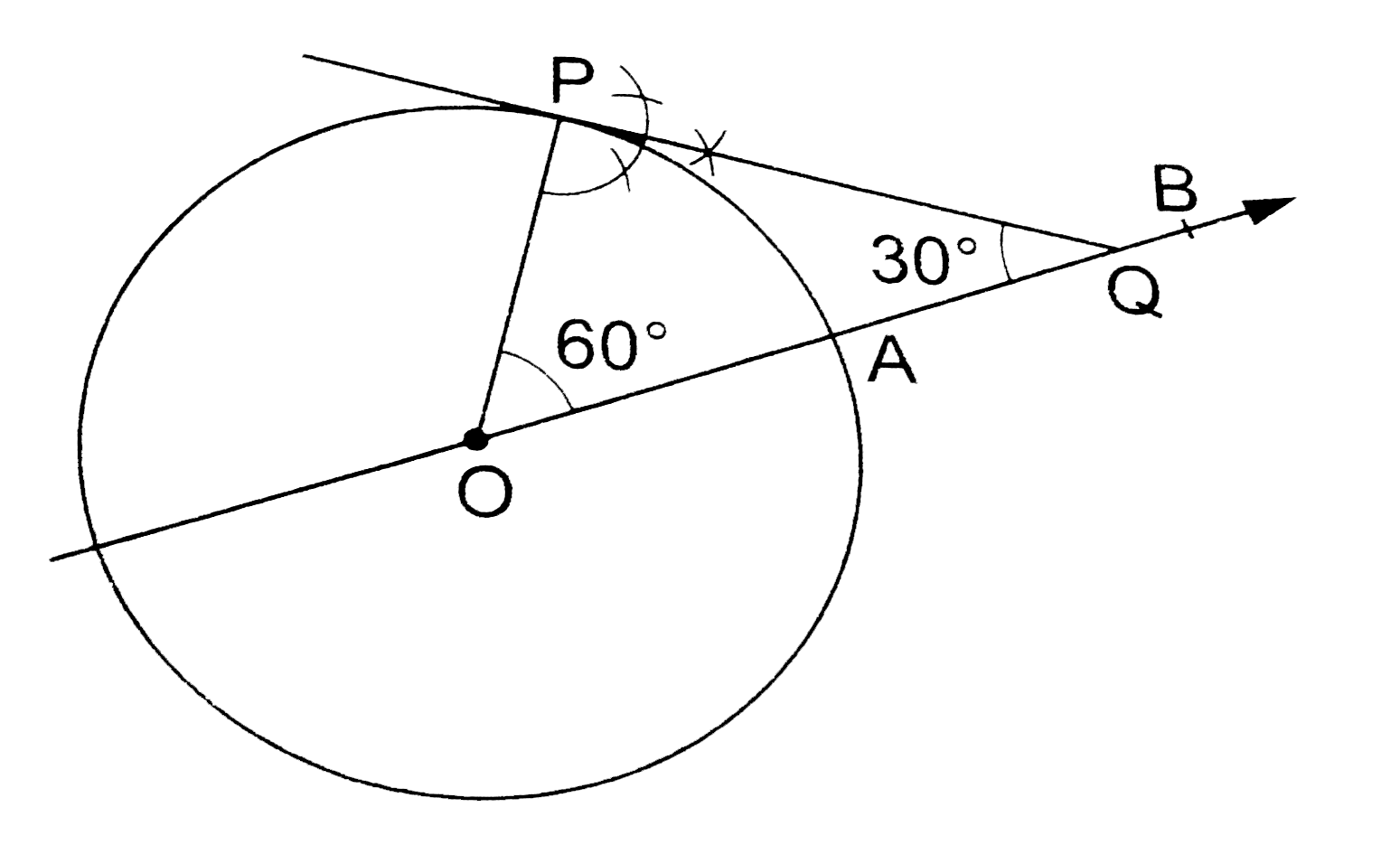
Discussion
3465.

Among D, F, J, P and A who reached office last? I. F and J reached office together. II. Only D and P reached office ahead of J.

Answer»

Solution :From I and II it is clear that only D and PREACHED office ahead of J and thus F. This implies that A reached last so the data in both I and II together are required to ANSWER the QUESTION.
Discussion
3466.

Two circles of radii 3 cm and 4.5 cm are drawn with their centres 5 cm apart. They are:

Answer»

CONCENTRIC CIRCLES
INTERSECTING circles
CONGRUENT circles
Non-intersecting circle

Answer :B
Discussion
3467.

Ashraf went to see a movie. He wanted to purchase a movie ticket for Rs. 80. As the ticket for Rs. 80 was not available, he purchased a ticket for Rs. 120 of upper class. How much extra GST did he pay for the ticket ? (GST for a ticket below Rs. 100 is 18% and GST for a ticket above Rs. 100 is 28%)

Answer»


ANSWER :RS. `19.20`
Discussion
3468.

A painter is given a task to paint a cubical box made of wood with three different colours: Red, Blue and Black with instructions that two opposite faces must have the same colour. He was asked to cut this box into 27 smaller cubes of equal size. Now answer the following questions. How many cubes will be there with two faces painted with blue and black colours?

Answer»

4
2
6
8

Solution :When opposite faces of a cube are painted with three different colours, note the following POINTS.
(i) Number of cubes with three colours on each will be 8.
(ii) Number of cubes with two colours on them, will be divided into three SETS (a) Blue, black (b) Red, blue and ( c) Red, black. Each set will have `1/3[12(X/x-2)]` cubes.
(iii) Number of cubes with one face coloured red, blue or black on them
= `1/3[6(X/x-2)]`.
Now we find the answers to the QUESTION. There are 27 cubes of smaller SIZE. If these cubes have 1 cm edge, the edge of the big cube is given by
`(X/1)^(3)=27`, so X = 3. Now use X = 3 and x = 1 in the above formulae :
The number of such cubes =
`1/3xx12(3/1-2)=4`.
Discussion
3469.

A painter is given a task to paint a cubical box made of wood with three different colours: Red, Blue and Black with instructions that two opposite faces must have the same colour. He was asked to cut this box into 27 smaller cubes of equal size. Now answer the following questions. How many cubes will be there with only one face painted blue?

Answer»

0
1
2
3

Solution :When opposite faces of a cube are painted with three different colours, note the following points.
(i) Number of cubes with three colours on each will be 8.
(ii) Number of cubes with two colours on them, will be divided into three sets (a) Blue, black (b) Red, blue and ( c) Red, black. Each SET will have `1/3[12(X/x-2)]` cubes.
(iii) Number of cubes with one face coloured red, blue or black on them
= `1/3[6(X/x-2)]`.
Now we find the ANSWERS to the question. There are 27 cubes of SMALLER size. If these cubes have 1 CM edge, the edge of the big cube is GIVEN by
`(X/1)^(3)=27`, so X = 3. Now use X = 3 and x = 1 in the above formulae :
The number of cubes painted blue
= `1/3{6(3/1-2)}=2`.
Discussion
3470.

A painter is given a task to paint a cubical box made of wood with three different colours: Red, Blue and Black with instructions that two opposite faces must have the same colour. He was asked to cut this box into 27 smaller cubes of equal size. Now answer the following questions. How many cubes will be there with all the three colours on them?

Answer»

3
6
8
9

Solution :When opposite faces of a cube are painted with three different colours, note the following points.
(i) Number of cubes with three colours on each will be 8.
(ii) Number of cubes with two colours on them, will be divided into three sets (a) Blue, BLACK (B) Red, blue and ( c) Red, black. Each set will have `1/3[12(X/x-2)]` cubes.
(III) Number of cubes with one face coloured red, blue or black on them
= `1/3[6(X/x-2)]`.
Now we FIND the answers to the question. There are 27 cubes of smaller size. If these cubes have 1 cm edge, the edge of the big cube is given by
`(X/1)^(3)=27`, so X = 3. Now USE X = 3 and x = 1 in the above formulae :
Discussion
3471.

A painter is given a task to paint a cubical box made of wood with three different colours: Red, Blue and Black with instructions that two opposite faces must have the same colour. He was asked to cut this box into 27 smaller cubes of equal size. Now answer the following questions. How many smaller cubes will be there with no face painted at all?

Answer»

6
8
4
1

Solution :When opposite faces of a cube are PAINTED with three different colours, note the following points.
(i) Number of CUBES with three colours on each will be 8.
(ii) Number of cubes with two colours on them, will be divided into three sets (a) Blue, black (B) Red, blue and ( c) Red, black. Each set will have `1/3[12(X/x-2)]` cubes.
(iii) Number of cubes with one face coloured red, blue or black on them
= `1/3[6(X/x-2)]`.
Now we find the answers to the QUESTION. There are 27 cubes of smaller size. If these cubes have 1 cm edge, the edge of the big cube is given by
`(X/1)^(3)=27`, so X = 3. Now use X = 3 and x = 1 in the above formulae :
Number of cubes with no face painted
`(X/x-2)^(3)-(3/1-2)^(3)=1`
Discussion
3472.

E is a point on the side AD produced of a parallelogram ABCD and BE inter seets CD at F, show that OR The permiters of two similar triangles ABC and PQR are respectively 36cm and 24cm. If PQ=10cm, find AB.

Answer»


ANSWER :15 CM
Discussion
3473.

Find the distance between the point (2,3) and (4,1) .

Answer»


ANSWER :`SQRT(74)`
Discussion
3474.

A train travels 360 km at a uniform speed. If the speed had been 5 km /h more, it would have taken 1 hour less for the same journey. Find the speed of the train.

Answer»


ANSWER :40 KMPH
Discussion
3475.

A cylinderical pencil is sharpened to produce a perfect cone at one end with no over all loss of its length. The diameter of the pencil is 1 cm and the length of the conical portion is 2 cm. Calculate the volume of the shavings. Give your answer correct to two places if it is in decimal. ["Use "pi=355/113]

Answer»


ANSWER :`1.05 cm^3`
Discussion
3476.

Prove that the opposite side of a quadrilateral circumscribing a circle subtend supplementary angles at the centre of the circle.

Answer»
Discussion
3477.

Find zeros of l(x) ,g(x) ,q(x), m(x) .

Answer»


Answer :L(X) is `(7)/(8)`
`g(x) are (3)/(2),(3)/(2)`
Q(x) are `pm sqrt(5)`
m(x) is `(sqrt(3))/(2)`
Discussion
3478.

If one zero of the quadratic polynomial (k^(2)+k)x^(2)+68x+6k is reciprocal of the other , find k.

Answer»


ANSWER :`5`
Discussion
3479.

What will be the number of zeros of a linear polynomial p(x) if its graph (i) passesthrough the origin. (ii) doesn't intersect or touch x-axis at any point ?

Answer»


ANSWER :`(i) 1` `(II) 0`
Discussion
3480.

Solve each of the following pairs of equations by reducing them to a pair of linear equations. (5)/(x-1)+(1)/(y-2)=2" and "(6)/(x-1)-(3)/(y-2)=1.

Answer»


ANSWER :(4,5)
Discussion
3481.

The slant and diameter of the base of a conical tomb are 25 m and 14 m respectively.Find the cost of painting its curved surface area at the rate of RS 50 per square meter.

Answer»


ANSWER :`=550xx50Rs27,500`
Discussion
3482.

Write the following expressions as log N and find their values. log 2 + log 5

Answer»


ANSWER :LOG 10,1
Discussion
3483.

Solve : (i) 2x^(2)-5x+3=0 (ii) (x^(2)+3x)^(2)-(x^(2)+3x)-6=0, xepsilonR

Answer»


ANSWER :(i) `1, -1, (sqrt(6))/(2)`, or `-(sqrt(6))/(2)`
(ii) `(-3+sqrt(21))/(2), (-3-sqrt(21))/(2), -1`, or `-2`
Discussion
3484.

A motor boat heads upstream a distance of 24 km in a river whose current is running at 3 km per hour. The trip up and back takes 6 hours. Assuming that the motor boat maintained a constant speed, what was its speed in still water?

Answer»


ANSWER :9 KMPH
Discussion
3485.

The value of lower limit (L) in the above example to calculate median is

Answer»

0
10
20
30

Answer :C
Discussion
3486.

A thief runs away from a police station with a uniform speed of 100 m/minute. After 1 minute a policeman runs behind the thief to catch him. He goes at a speed of 100 m/ minute in first minute and increases his speed by 10 m/ minute in each succeeding minute. How many minutes will the policeman take to catch the thief?

Answer»


ANSWER :SINCE n cannot be NEGATIVE, the time taken by the policeman to catch the thief = 5 minutes.
Discussion
3487.

If one zero of p(x)=4x^(2)-(8k^(2)-40k)x-9 is negative of the other, find values of k.

Answer»


ANSWER :`k=0,5`
Discussion
3488.

During the medical check -up of 35 students of a class , their weights were recorded as follows :{:("Weight (in kg)","Number of students"),("Less than "38,0),("Less than "40,3),("Less than "42,5),("Less than "44,9),("Less than "46,14),("Less than "48,28),("Less than "50,32),("Less than "52,35):} Draw a less than type ogiven for the given data . Hence obtain the median weight from the graph and verify the result by using the formula .

Answer»


ANSWER :X=2 UNITS , Y=4 units
Discussion
3489.

If finger is called toe, toe is called foot, foot is called thumb, thumb is called ankle, ankle is called palm and palm is called knee, which one finger has different name?

Answer»

THUMB
Ankle
Knee
Palm

Solution :CLEARLY the thumb is a FINGER having a different name. But .thumb. is called .ankle. So .ankle. is the finger that has a different name
Discussion
3490.

A toy is made in the form of hemisphere surmounted by a right cone whose circular base is joined with the plane surface of the hemisphere. The radius of the base of the cone is 7 cm. and its volume is 3/2 of the hemisphere. Calculate the height of the cone and the surface area of the toy correct to 2 places of decimal. ("Take "pi=3""1/7)

Answer»


ANSWER :`794.990 CM^(2)`
Discussion
3491.

Half the perimeter of a rectangular garden whose length is 4 m more than its width, is 36m. The dimensions of the garden are :

Answer»

26M, 10 m
20m, 16m
22m, 14m
None of these

Answer :B
Discussion
3492.

The value of (2^(1//2) xx 3^(1//3) xx 4^(1//4))/(10^(-1//5) xx 5^(3//5)) + (4^(-2//3) xx 5^(-7//5))/(4^(-3//5) xx 6^(-1//3)) is equal to

Answer»

10
1
6
18

Answer :A
Discussion
3493.

How many terms of the series 2+6+18+ . . . . . . . . . . . Must be taken to make the sum equal to 728 ?

Answer»


ANSWER :6
Discussion
3494.

If the distances of P(x, y) from the points A(3, 6) and B(-3, 4) are equal, prove that 3x + y = 5.

Answer»


ANSWER :`Y=5`
Discussion
3495.

A fex, the cap used by the Turks, is shaped like the frustum of a cone. If its radius on the open side is 10cm, radius at the upper base is 4cm and its slant height is 15cm, find the area of material used for making it.

Answer»


ANSWER :710.28 `CM^(2)`
Discussion
3496.

The volume of a cone with radius 7 cm and slant height 25 cm is ......... cm^(3)

Answer»


ANSWER :1232
Discussion
3497.

Ismail gets a monthly salary of Rs. 12,500. He contributes Rs. 3500 per month towards PF. Calculate the income tax paid by him.

Answer»

Rs. 3000
Rs. 5600
Rs. 4830
Rs. 3300

Solution :Deduct the SAVINGS (as per the NORMS) and STANDARD deduction from the ANNUAL salary.
Discussion
3498.

5 pencils and 7 pens together cost Rs.50 whereas 7 pencils and 5 pens together cost rs.46 Find the cost of one pencil and that of one pen.

Answer»


ANSWER :COST of PENCIL =Rs.3: Cost of PEN = Rs.5
Discussion
3499.

Shayam went to a stationary shop and purchased 2 pens and 3 pencils for Rs. 9. His friend Rahim saw the new variety of pens and pencils with Shyam and he also bought 4 pens and 6 pencils of the same kind for Rs. 18.(i) from the linear equation. (ii) Represent this situation graphically.(iii) Which person have been more beneficial ?

Answer»


ANSWER :(0,3), (3,1), (4.5, 0)
Discussion
3500.

In thefigure, the angle of elevation theta is

Answer»

`30^(@)`
`45^(@)`
`90^(@)`
`60^(@)`

ANSWER :A::C
Discussion