InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 851. |
Therange of f(x)=cos^(-1)((1+x^(2))/(2x))+sqrt(2-x^(2)) is |
|
Answer» `{0, 1 + PI/2}` |
|
| 852. |
The range of f(x)=cos^(-1)((1+x^(2))/(2x))+sqrt(2-x^(2)) is |
|
Answer» `{0, 1 + PI/2}` |
|
| 853. |
Find the locus of the point (a-bsectheta,a-btantheta) where theta is the parameter. |
|
Answer» |
|
| 854. |
Which of the following statements are true. Statement-I: (vec(r ).vec(i)) (vec(r )xx vec(i)) + (vec(r ).vec(j)) (vec(r ) xx vec(j)) + (vec(r ).vec(k)) (vec(r )xx vec(k)) = vec(r ) Statement-II: If vec(a) xx vec(b)= vec(0), vec(a).vec(b)=0, then one of vec(a),vec(b) is a null vector. |
|
Answer» only I |
|
| 855. |
If bara,barb are two vectors of length 2, 1 respectively and abs(bara-barb) = sqrt3, " then " (bara,barb)= |
|
Answer» `pi//4` |
|
| 856. |
A point in the XZ plane is ………a) (1,1,1)b) (2,0,3) |
|
Answer» `(1,1,1)` |
|
| 857. |
If bar(OP)=2bar(i)+3bar(j)-bar(k), bar(OQ)=3bar(i)-4bar(j)+2bar(k) then d.c's of bar(PQ) are |
|
Answer» `1/sqrt(59)(-1, 7, 3)` |
|
| 858. |
AB is a line of fixed length, 6 units, joining the points A (t, 0) and B which lies on the positive y-axis. P is a point on AB distant 2 units from A.Express the co-ordinates of B and P in terms of t. Find the locus of P as t varies. |
|
Answer» |
|
| 859. |
Write the converse, inverse and contrapositive of the following statements. If you do not drink your milk, you will not be strong. |
|
Answer» Inverse : If you drink your milk, then you are strong. Contrapositive : If you are strong, then you drink your milk . |
|
| 860. |
Position of the point (3,4) with respect to hyperbola x^(2) - 4y^(2) + 24y - 37 = 0 is ……….. |
|
Answer» INSIDE hyperbola |
|
| 863. |
Solve the equation: log_(2x+3)x^(2) lt log_(2x)(2x+3) |
Answer» SOLUTION :This inequation is EQUIVALENT to the collection of the systems 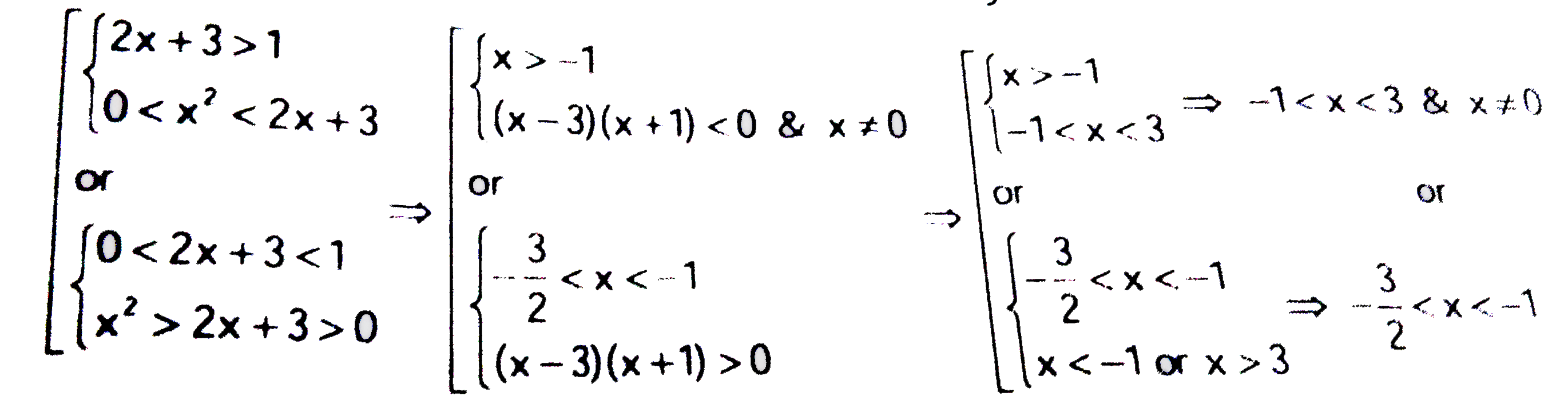 HENCE, solution of the original inequation is `x in (-3/2,-1) cup (-1,0) cup (0,3)` |
|
| 864. |
Sin^(-1)(xsqrt(1-y^(2))+ysqrt(1-x^(2)))= |
|
Answer» `SIN^(-1)X+sin^(-1)SQRT(x)` |
|
| 865. |
Examine Lim_(xto 2) [ x] , where [ x] denotes the greatest integarless than or equal to x. |
|
Answer» |
|
| 866. |
Find the derivative of w.r.to x sec (tan sqrtx) |
|
Answer» |
|
| 867. |
Let L_1: 3X+4Y-1=0and L_2 : 5z-12y+2=0 be two given lines. Let image of every point on L_1 w.r.t a line L lies on L_2 then possible equation of 'L' can be |
|
Answer» `14x+112y-23=0 |
|
| 868. |
(cos h2 + sin h 2)^(n) = |
|
Answer» `COS H(2N) + SIN (2n)` |
|
| 869. |
The range of f(x)=(1-tan x)/(1+tan x) is |
|
Answer» `(-OO, oo)` |
|
| 870. |
If alpha, beta, gamma are the angles made by a line with the positive directions of the coordinate axes, then sin^(2)alpha+sin^(2)beta+sin^(2)gamma= |
|
Answer» |
|
| 871. |
Find the value of the expression sqrt3 cosec 20^@-sec20^@=……. |
|
Answer» 2 |
|
| 872. |
Show that the function f(x) = 2x^(2) - 3(lambda + 2) x^(2) + 2 lambdax + 5 has one maximum and one minimum for all lambda in R |
|
Answer» |
|
| 873. |
In which ratio XY plane divides line segment joining points (2, 4, -3) and (-3, 5, 4). |
|
Answer» |
|
| 874. |
If the projections of a line segment on the axes are 3, -4, 12 then the length of the segment and d.c.'s of the line are |
|
Answer» |
|
| 875. |
Write each sentence in the " If ................Then " form. Any two parallel lines are coplanar. |
|
Answer» |
|
| 876. |
A class consists of 100 students, 25 of them are girls and 75 boys, 20 of them are rich and remaining poor, and 40 of them are fair-complexioned. Probability of selecting a fair-complexioned rich girl from this class is |
|
Answer» `0.02` |
|
| 877. |
Theperiodof sin ((pi x )/( 2 )) + 2 cos((pi x)/(3 ) ) - tan((pi x)/(4))is |
|
Answer» 4 |
|
| 878. |
Find the value of n if: (i) (n+2)! = 12. n! (ii) (n+2)! = 60-. (n-1)! =({2.4.6....(2n)}{1.3.5....(2.-1)})/(n!) = (2^(n){1.2.3...n}{1.3.5.......(2n-1)})/(n!) = 2^(n) {1.3.5....(2n-1)} = R.H.S. Hence Proved. (iii) (n+3)! = 2550 (n+1)! (iv) (n-2)! = 132. (n-4)!. |
|
Answer» |
|
| 879. |
A polygon of nine sides, each side of length 2, is inscribed in a circle. The radius of the circle is..... |
|
Answer» `sec(pi/9)` |
|
| 880. |
Find the coordinates of the points which trisect the line segment joining the points P(4,2,-6) and Q(10,-16,6). |
|
Answer» |
|
| 881. |
If the range of the functionf(x) = ((1+x+x^(2))(1+x^(4)))/( x^(3)) " when "x gt0is[K, infty )then K is |
|
Answer» |
|
| 882. |
An open recangular tank with a square base and 32 c.c of capacity has least surface aren in sq. cms is |
|
Answer» 48 |
|
| 883. |
If sin^(2) x tan x + cos ^(2) x cot x - sin 2 x = 1 + tan x + cot x x in (0, pi) then x = |
|
Answer» `(3 pi)/( 12), (5 pi)/(12)` |
|
| 884. |
(i)Suppose8 peopleenteran eventin a swimmingmeet. In how manywayscouldthe gold, silverand bronzeprizes be awarded ? (ii)Three menhave4 coats , 5waist coats and 6 caps. In howmany wayscan they wearthem ? |
|
Answer» (II)172800 |
|
| 885. |
A lette is chosen at random from the 'ASSASSINATION'. Find the probability that letter is (i) a vowel (ii) a consonant. |
|
Answer» |
|
| 887. |
Let A= {1, 2, 3}, B= {3, 4} and C= {4, 5, 6}. Find (A xx B) nn (A xx C) |
|
Answer» |
|
| 888. |
If l_(1), m_(1), n_(1) and l_(2), m_(2), n_(2) are the direction cosines of two vectors and theta is the angle between them, then the value of cos theta is |
|
Answer» `SIN theta=l_(1)-l_(2)` |
|
| 889. |
If Deltarepresents the area of acute angled triangle ABC, then sqrt(a^(2)b^(2)-4Delta^(2))+ sqrt(b^(2)c^(2)-4Delta^(2))+sqrt(c^(2)a^(2)-4Delta^(2))= |
|
Answer» `a^(2)+B^(2)+c^(2)` |
|
| 890. |
if ""^nc_(r-1)=36, ""^nc_r=84 and ""^nc_(r+1)=126,than find the value of ""^rc_(2. |
|
Answer» |
|
| 891. |
cos^(4)alpha+sin^(4)alpha-6sin^(2)alpha cos^(2)alpha= |
|
Answer» `COS 2ALPHA` |
|
| 892. |
Consider the compound statements ''35 is divisible by 5 or 6''Write the truth values of the compound statement and the component statements given above |
| Answer» SOLUTION :T,T,F RESPECTIVELY] | |
| 893. |
If AD, BE and CF are the medians of a triangle ABC, then AD^(2) + BE^(2) + CF^(2) :BC^(2)+CA^(2)+AB^(2)is equal to |
|
Answer» `4 : 3 ` |
|
| 894. |
The remainder when 2^(2020) is divided by 15 is |
|
Answer» 4 |
|
| 895. |
The scores of two golfers for 10 rounds each are: Which may be regarded as the more consistent player? |
|
Answer» |
|
| 897. |
A committee of 5 is to be formed from a group of 10 people consisting 4 single men 4 single women and a married couple. The committee is to consist of a chairman , who must be a single man 2, other men and 2 women, Find the total number of committes possible. |
|
Answer» |
|
| 898. |
A committee of 5 is to be formed from a group of 10 people consisting 4 single men 4 single women and a married couple. The committee is to consist of a chairman , who must be a single man 2, other men and 2 women, How many of these would include the married couples? |
|
Answer» |
|
| 899. |
If (4k _(1), k _(2) ^(2) , 1) and ( 4k _(2) , k _(2) ^(2), 1) are two points lying on the plane in which (2,3,2) and (1,2,1) are mirror image to each other, then k _(1) k _(2) is equal to |
|
Answer» `-3/2` |
|