InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 2802. |
Find the slope of the time passing through the points (3,-2) and ( -1,4) |
|
Answer» |
|
| 2803. |
If the ratio of the sums of m terms and n terms of an A.P. be m^(2) : n^(2), prove that the ratio of its m^(th) and n^(th) terms is (2m-1) : (2n-1). |
|
Answer» |
|
| 2804. |
Evaluate the following limits : Lim_(x to a) (xsqrt(x)-asqrt(a))/(x-a) |
|
Answer» |
|
| 2805. |
If.^(n)C_(12) =^(n)C_(8)then n = . . . . . |
|
Answer» 12 |
|
| 2806. |
If bara,barb,barc " are three mutually perpendicular vectors such that " absbara = absbarb = absbarc, " then " (bara+barb+barc,bara)= |
|
Answer» `pi//3` |
|
| 2807. |
If bar(a), bar(b)&bar(c) are non-coplanar vectors and if bar(d) is such that bar(d)=1/x(bar(a)+bar(b)+bar(c)) and bar(d)=1/y(bar(b)+bar(c)+bar(d)) where x and y are non-zero real numbers, then 1/(xy)(bar(a)+bar(b)+bar(c)+bar(d))= |
| Answer» Answer :C | |
| 2808. |
3sinx+4cosx-6=0 then the general solution of x = |
|
Answer» `NPI+(-1)^(n)(pi)/(6)` |
|
| 2809. |
Find (x + 1)^6 + (x-)^6. Hence or otherwise evaluate (sqrt2 + 1)^6 + (sqrt2 - 1)^6. |
|
Answer» |
|
| 2810. |
A coin is tossed twice, what is the probability that at least one tail occurs? |
|
Answer» |
|
| 2811. |
What is the number of terms in the expansion of the following? (6x- (1)/(x^3) )^(17) |
|
Answer» |
|
| 2813. |
If the real part of (barz+2)/(barz-1) is 4 then show that the locus of the point representing z in the complex plane is circle. |
|
Answer» |
|
| 2815. |
If one angle of a triangle is 30^(@) and the lengths of the sides adjacent to it are 40 and 40sqrt(3), then the triangle is |
|
Answer» EQUILATERAL |
|
| 2816. |
The set of all x for which sin x lex is |
|
Answer» `(0,(PI)/(2))` |
|
| 2817. |
If the 4^(th) and 7^(th) term of a G.P. are 27 and 729 respectively, then find the G.P. |
|
Answer» |
|
| 2818. |
If f: R rarr R is a function such that f(x +y) =f(x) +f(y) forall x,y in R then f is continuous on R if it is continuous at a single point in R. |
|
Answer» |
|
| 2819. |
Find the area of the triangle formed by the lines y-x =0, x+y=0 and x-k=0. |
|
Answer» |
|
| 2820. |
Find the shortest distance between the lines (x-3)/(3)=(y-8)/(-1)=(z-3)/(1) and (x+3)/(-3)=(y+7)/(2)=(z-6)/(4) |
|
Answer» `sqrt30` |
|
| 2821. |
Find the derivative of the following functions: 5sin x-6 cosx+7 |
|
Answer» |
|
| 2822. |
Statement- I The soluton of the system of equations 2x-y+3z=9,x+y+z=6,x-y+z=2 is x=1,y=2,z=3 Statement- II : The solution of the system of equations x+2y-z=3,3x=y+2z=1, 2x-2y+3z=2 is x=-1,y=4,z=4 Which of the above Statement(s) is true ? |
|
Answer» only I is TRUE |
|
| 2823. |
A straight line through the point (3,4) in the first quadrant meets the axes at A and B . The minimum area of the triangle OAB is |
|
Answer» 42 |
|
| 2824. |
A plane which passes through the point (3,2,0) and the line (x-4)/(1) = (y-7)/(5) = (z-4)/(4) is |
|
Answer» `X - y + Z=1` |
|
| 2825. |
(2n+7) lt (n+3)^(2) |
|
Answer» Solution :For n=1 L.H.S `=2xx1+7=9` R.H.S. `=(1+3)^(2)=16` `:. ""L.H.S. LT R.H.S.` `RARR` Given statement is true for n=1 LET given statement be true for n=k `:. ""2k+7 lt (k+3)^(2)` for n=K+1 `2(k+1)+7 =(2k+7)+2` `lt (k+3)+2` [From inequation (1)] `=K^(2)+6k+11` `lt (k^(2)+6K+11)+(2k+5)` `lt K^(2)+8K+16lt (k+4)^(2)` ` rArr 2(k+1) +7 lt (K+4)^(2)` `rArr` Given statement is also true for n=K+1 HENCE from the principle of mathematical induction P (n) is true for all natural numbes n. |
|
| 2827. |
Given that 1-costheta=2sin^2(theta/2) and 1+costheta=2cos^2(theta/2) prove that(1+sintheta-costheta)/(1+sintheta+costheta)=tan(theta/2) |
| Answer» SOLUTION :`sqrt2-1` | |
| 2828. |
d/(dx)[tanh^(-1)((2x)/(1+x^2))]= |
|
Answer» `2/(1-x^2)` |
|
| 2829. |
A window is in the shap of a rectangle surmounted by a semicircle. If the perimeter of the window is 20 ft, find the maximum area. |
|
Answer» |
|
| 2830. |
The plane which passes through the point (3,2,0) and the line (x-3)/(1) = (y-6)/(5) = (z-4)/(4) is |
|
Answer» `X - y + z =1` |
|
| 2831. |
Express each of the following in the form (a + ib) : {:((i),(1)/((4+3i)),(ii),((3+4i))/((4-5i)),(iii),((5+sqrt(2)i))/((1-sqrt(2)i))),((iv),((-2+5i))/((3-6i)),(v),((3-4i))/((4-2i)(1+i)),(vi),((2-2i)(2+3i))/((1+2i)(2-i))),((vii),((2+3i))/((2-i)),(viii),((1-i)^(3))/((1-i^(3))),(ix),((1+2i)^(3))/((1+i)(2-i))):} |
|
Answer» |
|
| 2832. |
Find the direction in which a straight line must be drawn through the point (-1,2) so that its point of intersection with the line x+y=4 may be at a distance of 3 units from this point. |
Answer» Solution :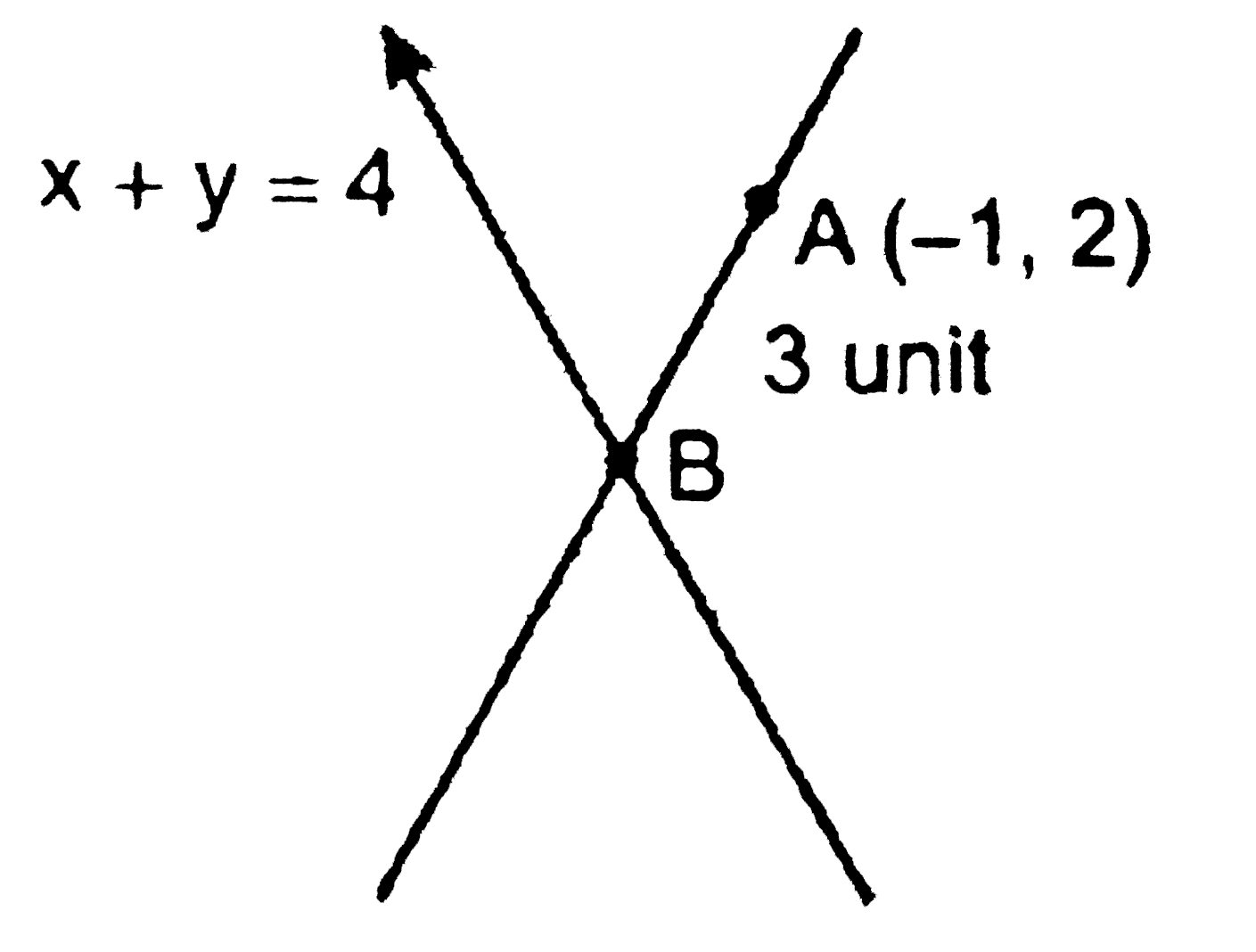 Let the slope of REQUIRED line PASSING through the point `(-1,2)` is `m`. `,.` Equation of line is, `y-2=m(x+1)` `impliesmx-y=-2-m`…….`(1)` Given line is, `x+y=4`……..`(2)` Solving we get `x=(2-m)/(m+1)` and `y=(5m+2)/(m+1)` `:.` Point of intersection is , `B=((2-m)/(m+1),(5m+2)/(m+1))` Given that `AB=3` units `impliessqrt(((2-m)/(m+1)+1)^(2)+((5m+2)/(m+1)-2)^(2))=3` `impliessqrt(((3)^(2)+(3m)^(2))/((m+1)^(2)))=3` `implies 3^(2)+9m^(2)=9(m+1)^(2)` `implies 9+9m^(2)=9m^(2)+18m+9` `implies 4m+18m=0` `impliesm=0` Now, `m=0` then `TAN theta=0impliestheta=0^(@)` `implies` Line is parallel to `x`-axis. |
|
| 2833. |
Assertion (A): tan40^(@) + tan 80^(@) - sqrt(3)tan 40^(@) tan80^(@)=-sqrt(3) Reason( R): tan( A + B) =tan A + tan B + tan(A + B) tan A tan B |
|
Answer» A is TRUE, R is true and R is correct EXPLANATION of A |
|
| 2834. |
Find the valueof r , if the coefficients of (2r+4)th and (r-2) th terms in the expansion of (1+x)^(18) are equal . |
|
Answer» |
|
| 2835. |
if a_(n) = sqrt(7+sqrt(7+sqrt(7 +n….))) times, then which one of the following is true ? |
|
Answer» `a_(n) gt 7, AA n GE 1` |
|
| 2836. |
If the pair of lines x^2+2xy+ay^2=0 and ax^2+2xy+y^2=0 have exactly one line in common, then the joint equation of the other two lines is given by |
|
Answer» `3x^2+8xy-3y^2=0` |
|
| 2837. |
The number of ways in which 6 men and 5 women can dine at a round table if no two women are to sit together is given by. |
|
Answer» ` 6! XX 5! ` |
|
| 2838. |
If f(x) satisfies Rolle's theorem for f(x) in [a,b] then int_(a)^(b) f'(x) dx = |
| Answer» Answer :D | |
| 2839. |
A plane which passes through the point (3,2,0) andthe line (x-4)/(1) = (y-7)/(5) = (z-4)/(4) is |
|
Answer» `X - y + z =1` |
|
| 2840. |
If a_(1)Cos theta+b_(1) Sin theta+c_(1)=0 and a_(2) cos theta+ b_(2) sin theta +c_(2)= 0 then (b_(1)c_(2)-b_(2)c_(1))^(2)+(c_(1)a_(2)-c_(2)a_(1))^(2)= |
|
Answer» `(a_(1)b_(2)-a_(2)b_(1))^(2)` |
|
| 2841. |
y=sin""(x)/(2),x in[0,2pi]. The function y is ………. In (0,pi). |
|
Answer» DECREASING |
|
| 2842. |
The radius and height of a cylinder are measured as 5 cm and 10 cm respectively and there is an error of 0.02 cm in both the measurements. The percentage error in volume is |
|
Answer» 1 |
|
| 2844. |
In a DeltaOAB The P.V.'s of A, B are bar(a), bar(b) respectively. The P.V. of 'C' is (3bar(a))/4+bar(b)/2 then 'C' lies |
|
Answer» |
|
| 2845. |
How many different words can be formed by using all the letters of the word MATHEMATICS ? In how many of them, vowels are always together ? |
|
Answer» |
|
| 2846. |
The sum of coefficients of the two middle terms in the expansion of (1+x)^(2n-1) is equalto (2n-1)C_(n) |
|
Answer» |
|
| 2847. |
The sum of the solutions of the equation 2sin^(-1)sqrt(x^(2)+x+1)+cos^(-1)sqrt(x^(2)+x)=(3pi)/2 is |
|
Answer» 0 |
|
| 2848. |
For any two complex numbers z_(1) and z_(2), prove that Re (z_(1)z_(2)) = Re z_(1) Re z_(2)- 1mz_(1) Imz_(2) |
|
Answer» |
|