InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 4151. |
Using binomial theorem prove that 8^(n) - 7n always leaves remainder f when divided by49 for all positive integer n. |
|
Answer» |
|
| 4152. |
If A and B are acute angles such that sinA = sin^(2) B,cos^(2) A = 3 cos^(2) B then |
|
Answer» `A = pi//6` |
|
| 4153. |
The minute hand of a watch is 1.5cm long. How far does it tip move in 40 minute? (Use pi=3.14) |
|
Answer» |
|
| 4154. |
Evaluate the following limits in Exercises lim_(xto(pi)/(2))(tan2x)/(x-(pi)/(2)) |
|
Answer» |
|
| 4155. |
Find the component statements of the following compound statements: Number 7 is prime and odd. |
|
Answer» <P> q: odd number. |
|
| 4156. |
In trianle ABC, CD is the bisector of the angle C. if cos . C/2 = 1/3and CD = 6, then the value of (1/a + 1/b) = 1/lambda , " then " lambda is |
|
Answer» 3 |
|
| 4157. |
Show that x^(2)-y^(2)+x-3y-2=0repersent a pair of straight lines. Find also angle between the lines |
|
Answer» |
|
| 4158. |
The mean and standard deviation of 20 observations are found to boe 10 and 2 respectively.On rechecking it was found that on observation 8 was incorrect.Calculate the correct mean and the standard deviation in each of the following cases.(ii)if it replaced by 12. |
|
Answer» |
|
| 4159. |
Find the number of solutions of tanx + secx = 2cosx in [0,2pi] |
|
Answer» Solution :Here, `tanx + secx = 2cosx rArr SINX +1=2cos^(2)x` `rArr 2SIN^(2)x+sinx-1=0 rArr sinx=1/2, -1` But `sinx=-1 rArr x=(3pi)/(2)` for which `tanx+secx =2 cosx` is not DEFINED. THUS, `sinx=1/2 rArr x=pi/6, (5pi)/(6)` `rArr` number of solutions of `tanx+secx = 2cos x` is 2.Ans. |
|
| 4160. |
Differentiate the following w.r.t. x or t or u as the case may be: 11. y= (x^2 + 2x +5)/( x^3 + 2x + 4) |
|
Answer» |
|
| 4161. |
Determine if f defined by f(x)={{:(x sin""(1)/(x)," if "x ne 0),(0," if "x= 0):} is a continuous function? |
|
Answer» |
|
| 4162. |
If 1/2 le x le 1, thencos^(-1)x+cos^(-1)(x/2+1/2sqrt(3-3x^2)) is equal to |
| Answer» Answer :C | |
| 4163. |
Find the conditions that the line (i) y = mx + c may touch the circle x^(2) +y^(2) = a^(2) , (ii) y = mx + cmay touch the circle x^(2) + y^(2) + 2gx + 2fy + c = 0. |
|
Answer» |
|
| 4164. |
0.7625 xx 0.000357 |
|
Answer» |
|
| 4167. |
Find the equation of line intersecting the x-axis at a distance of 3 units to the left of origin with slope -2. |
|
Answer» |
|
| 4168. |
Write the first five terms of each of the sequenceswhose n^(th)terms are: a_(n) =n(n^2+5)/4 |
|
Answer» |
|
| 4169. |
A person standing at a junction (crossing) of twostraight paths represented by the equations 2x-3y+4=0 and 3x+4y-5=0 seek to reach the path whose equation is 6x-7y+8=0 in the least times. Find the equation of the path that he should follow. |
|
Answer» |
|
| 4170. |
Evaluate the following limits in Exercises lim_(xto-2)((1)/(x)+(1)/(2))/(x+2) |
|
Answer» |
|
| 4172. |
x + y ge 24,2x + y ge 32, x ge 0, y ge 0 |
Answer» 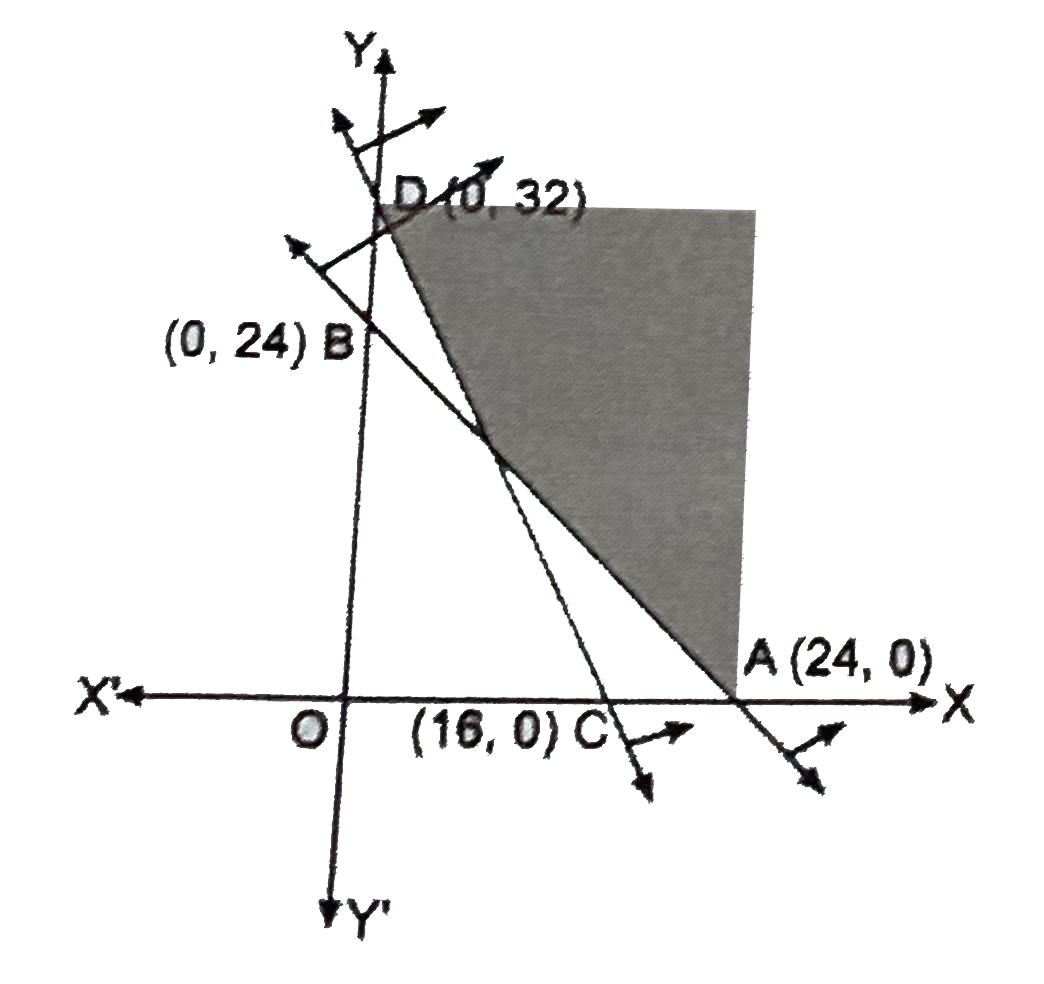
|
|
| 4173. |
The orthocentre of the triangle formed by the lines x+3y-10 and 6x^(2)+xy-y^(2)=0 is |
| Answer» ANSWER :A | |
| 4174. |
Consider the lines L _(1) : (x +1)/( 3) = (y+2)/(1) = (z+1)/(2), L_(2): (x-2)/(1) = (y+2)/(2) = (z-3)/(3) The unit vector perpendicular to both L _(1) and L _(2) is |
|
Answer» `(-hati + 7 hatj + 7 HATK)/(sqrt99)` |
|
| 4175. |
150 workers were engaged to finish a job in a certain number of days. 4 workers dropped out on second day, 4 more workers dropped out on third day and so on. It took 8 more days to finish the work. Find the number of days in which the work was completed. |
|
Answer» |
|
| 4176. |
A plane pi passes through the point (1,1,1) If b ,c,a are the dr' s of a normal to the pane, where a,b,c(a lt b lt c) are the prime factors of 2001, then the equation of the plane pi is |
|
Answer» `29 x + 31 y + 3Z = 63` |
|
| 4177. |
Evaluate the following limits : Lim_(x to 0) (a^(x) - b^(x))/(sin x) |
|
Answer» |
|
| 4178. |
Prove the following identieties using the theory of permutation where C_(0),C_(1),C_(2),……C_(n) are the combinatorial coefficents in the expansion of (1+x)^n,n in N: ""^(100)C_(10)+5.""^(100)C_(11)+10 .""^(100)C_(12)+ 10.""^(100)C_(13)+ 10.""^(100)C_(14)+ 10.""^(100)C_(15)=""^(105)C_(90) |
| Answer» | |
| 4179. |
Let T= {x|(x+5)/(x-7)-5 = (4x-40)/(13-x)}. Is T an empty set ? Justify your answer. |
|
Answer» |
|
| 4180. |
Find the sum of: 24 terms and n terms of 2 (1)/(2) , 3 (1)/(3) , 4 (1)/(6) ,5 ,......, |
|
Answer» |
|
| 4181. |
If u_(n)=2Cos^(n) theta then show that u_(1)u_(n)-u_(n-1)= u_(n+1) |
| Answer» | |
| 4182. |
If (1+tantheta)(1+tanphi)=2 then theta+phi = |
|
Answer» `30^(@)` |
|
| 4183. |
Let a, b, g be the distinct real numbers. The points with position vectors abar(i)+b""bar(j)+gbar(k), b""bar(i)+gbar(j)+abar(k), gbar(i)+abar(j)+b""bar(k) are |
|
Answer» Collinear |
|
| 4184. |
If f: R to R, g : R to R are defined by f(x) = 4x-1 and g(x) = x^(2)+2, then find (i) (gof)(x) (ii) (gof)(a+1)/4, (iii) (fof)(x), (iv) (go(fof))(0) |
|
Answer» |
|
| 4185. |
Evaluate the following limits : Lim_(x to 2) (x-2)/(sqrt(x)-sqrt(2)) |
|
Answer» |
|
| 4186. |
Let P be (5,3) and a point R on y=x and Q on the x-axis be such that PQ+QR+RP is minimum. The the coordinates of Q are |
|
Answer» `(17//4,0)` |
|
| 4187. |
y = "tan"^(-1)((sqrt(1 + a^2x^2 ) - 1)/(ax)) implies (1 + a^2x^2)y^('') + 2a^2 xy^'= |
|
Answer» `a^2` |
|
| 4188. |
Show that the vectors 2hati-hatj+hatk,hati-3hatj-5hatkand3hati-4hatk form the vertices of a right angled triangle. |
|
Answer» |
|
| 4189. |
If y=8x^(3)-60x^(2)+144x+57 is a decreasing function in the interval (a,b) , then (a,b) is |
|
Answer» `(-3,2)` |
|
| 4190. |
The set of values of 'b' for which the origin and the point (1,1) lie on the same side of the striaght line a^2x+aby+1=0,AAa in R, bgt0 are |
| Answer» Answer :B | |
| 4191. |
d/(dx)[log_(e) {(e^x + 2) + sqrt(e^(2x )+ 4e^x+ 5))}] = |
|
Answer» `1/(sqrt(E^(2x) + 4e^(x) + 5))` |
|
| 4192. |
The semivertical angle of the cone of maximum volume and of given slant height is |
|
Answer» |
|
| 4193. |
If barb=4bari+3barj and barc be two perpendicular vectors in xy-plane. The vector in the same plane having components 1, 2 along barb and barc respectively, is |
|
Answer» `2bari-barj` |
|
| 4194. |
If bar(a), bar(b), bar(c) are non coplanar vectors and lambda is a real number, then the vectors bar(a)+2bar(b)+3bar(c), lambdabar(b)+4bar(c) and (2lambda-1)bar(c) are non-coplanar for |
|
Answer» All VALUES of `lamda` |
|
| 4195. |
A tower, of x metres high, has a flagstaff at its top. The tower and the flagstaff subtend equal angles at a point distant y metres from the foot of the tower. Then the length of the flagstaff in metresis |
|
Answer» `(y(X^(2)-y^(2)))/((x^(2)-y^(2)))` |
|
| 4196. |
If Tan70^(@) - Tan20^(@) = k Cot40^(@) then k = |
|
Answer» -2 |
|
| 4197. |
Which of the above statements is correct. IIn a DeltABC if 4s(x-a)(s-b)(s-c)=a^(2)b^(2) then it is angled triangle. In a DeltABC the expression sinA+sinB+sinC is maximum then the triangle is equilaterl |
|
Answer» onlyI |
|
| 4198. |
For all positive integers n gt 1, { x(x^(n-1) - n,a^(n-1) ) } + a^(n) (n-1) } is divisible by |
|
Answer» `(x-a)^(2)` |
|
| 4199. |
What will Rs. 500 amounts to in 10 years after its deposit in a bank which pays annual interest rate of 10% compounded annually? |
|
Answer» |
|
| 4200. |
AA t in R, …….is the point lies on parabola x^(2) = 4ay. |
|
Answer» `X = at^(2) , y = 2AT` |
|