InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5651. |
Which of the following radical(s) on reaction with dil HCl liberate(s) gas which decolourize(s) acidified KMnO_(4) solution. |
|
Answer» `S_(2)O_(3)^(2-)`<BR>`NO_(2)^(-)` 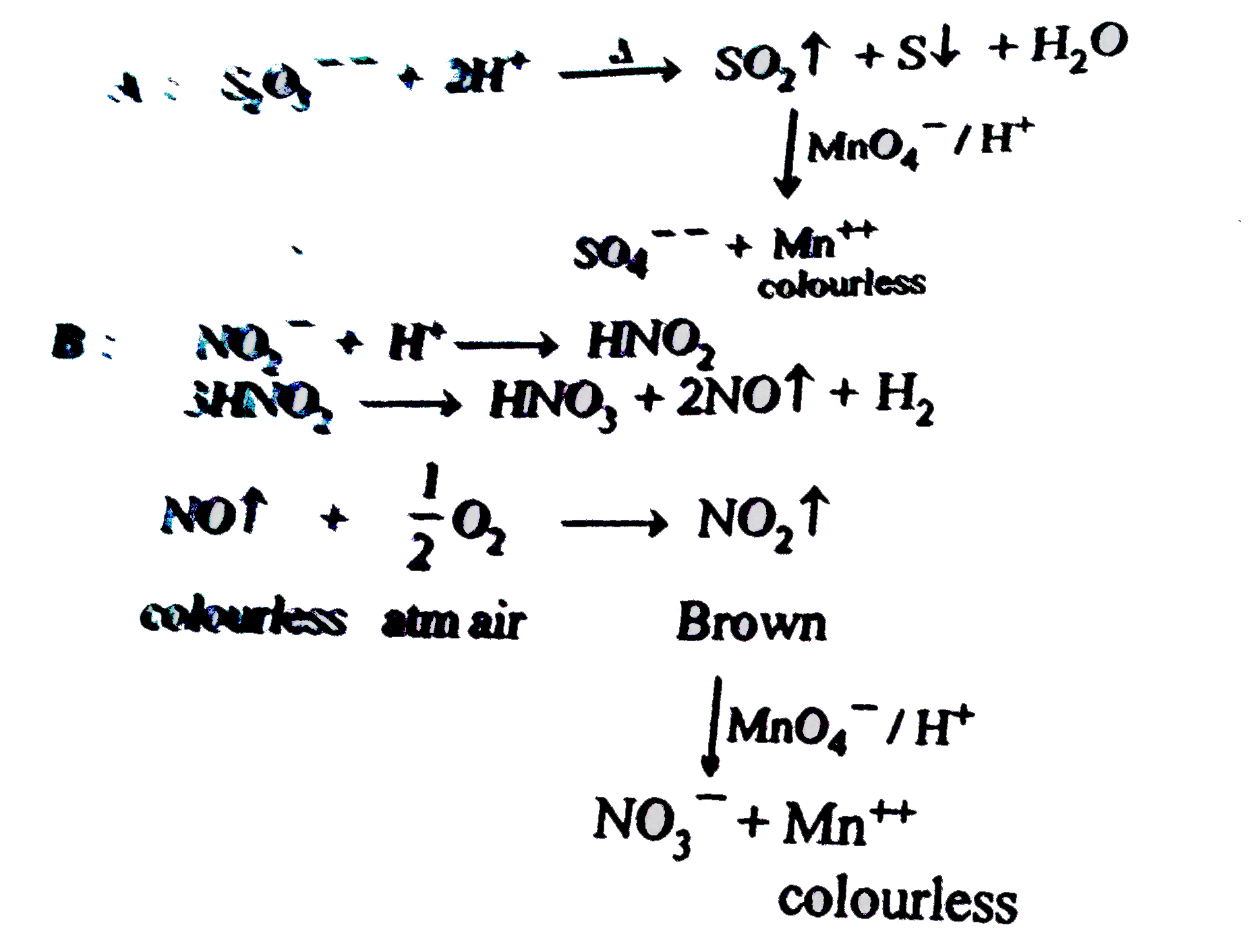
|
|
| 5652. |
Let g(x)=(e^((1)/(x)-1))/(e^((1)/(x)+1))"for " x ne0 andg (0) =0 Statement - I : The functions f (x )="xg"(x),xin RR is not derivable at x = 0 Statement - II underset(xrarr0)(lim"g(x) does not exist . |
|
Answer» Statement -I is TRUE , Statement -II is True , Statement -II is a CORRECT explanation for statement -I |
|
| 5653. |
A definite amount of an ideal gas (gamma = 1.5) undergoeschange of state in which heat exchangeis equal to work done (q=w). Molar heat capacity of the gas is : |
|
Answer» 2R |
|
| 5654. |
The partial fractions of ((x^(2)-1))/(x(x^(2)+1)) are |
|
Answer» `1/X + (2X)/(x^(2)+1)` |
|
| 5655. |
How many 4 digited numbers can be formed using 0, 1, 2,3,4 when repetition is allowed. |
|
Answer» |
|
| 5656. |
If the matrix A is both symmetric and skew-symmetricx then____ |
|
Answer» A is a DIAGONAL matrix |
|
| 5657. |
Solve system of linear equations, using matrix method in examples 7 to 142x+3y+3z=5 x-2y+z=-4 3x-y-2z=3 |
|
Answer» |
|
| 5658. |
Find the area of the triangle with vertices at(-2,-3),(3,2),(-1,-8) using determinants. |
| Answer» SOLUTION :15 SQ. UNITS | |
| 5659. |
If x-2y-a = 0 is a chord of y^(2) = 4ax then its length is |
|
Answer» `4sqrt(5)` a |
|
| 5660. |
The marginal revenue function of a commodity is MR = 9 + 2x - 6x^(2), find the total revenue function. |
|
Answer» |
|
| 5661. |
Solve : x dy= (y+x " cos"^(2)(y)/(x))dx |
|
Answer» `tan((y)/(x)) = LOG (CX)` |
|
| 5662. |
Define f(x) = (1)/(2)[|sinx|+sin x], 0 lt x le 2pi. Then f is |
|
Answer» Increasing in `((PI)/(2), (3 pi)/(2))` |
|
| 5663. |
Let A = ((0,x,0),(y,0,-x),(0,y,0)) then A^(3) equals |
|
Answer» O |
|
| 5664. |
Using molar concentrations, what is the unit of K_(c) for the reaction ? CH_(3)OH(g) hArr CO(g) + 2H_(2)(g) |
| Answer» Answer :A | |
| 5665. |
Area (in sq. units) of the triangle formed by the lines x^(2)+ 4xy+ y^(2)=0 and x+y=1 is |
| Answer» ANSWER :D | |
| 5666. |
If I_(1)=int_(0)^(x) e^("zx "e^(-z^(2)))dz and I_(2)=int_(0)^(x) e^(-z^(2)//4)dz, them |
|
Answer» `I_(1)=e^(x)I_(2)` |
|
| 5667. |
The number of ways of 5 letters put in 5 addressed envelopes so that one letter is in right envelop and all the remaining are placed in wrong envelopes is |
|
Answer» 45 |
|
| 5668. |
Dominickcollectedeigth differentsamples of mango juicefromdifferentbrands . Henotedthe concentrationof eachsampleand tabulatedthe results asfollows : A 'shot' refers toa mixtureformedusing2 distinctsampleis someproportion . How manysuchcombinations of samplemay Dominickuse toprepare'shots'with exactly 60% average 60% averageconcentration ? |
|
Answer» 5 |
|
| 5669. |
Number of roots f(x)=0 " in"[-2,2] is |
|
Answer» 0 |
|
| 5670. |
If f'(x)= e^x+1/(1+x^2),what is f(x) ? |
| Answer» Solution :F(x)= `e^x+1/(1+x^2)impliesf(x)=INT(e^x+1/(1+x^2))dx e^x+tan^(-1)x+c` | |
| 5671. |
Find (dy)/(dx)," if "x= a(theta+ sin theta), y= a(1- cos theta). |
|
Answer» |
|
| 5673. |
intx^(3).e^(x^(2))dx=..........+c |
|
Answer» `((x^(2)+1)/(2))e^(x^(2))` |
|
| 5675. |
Find the sum of roots the equation cos^(-1)(cos x)=[x],[*] denotes the greatest integer funtions. |
|
Answer» Solution :We have `cos^(-1)(cos X)=[x]` To FIND the ROODS of the equation, we DRAW the graphs of `y=cos^(-1)(cos x)" and "y = [x]` and then find the points of intersection. 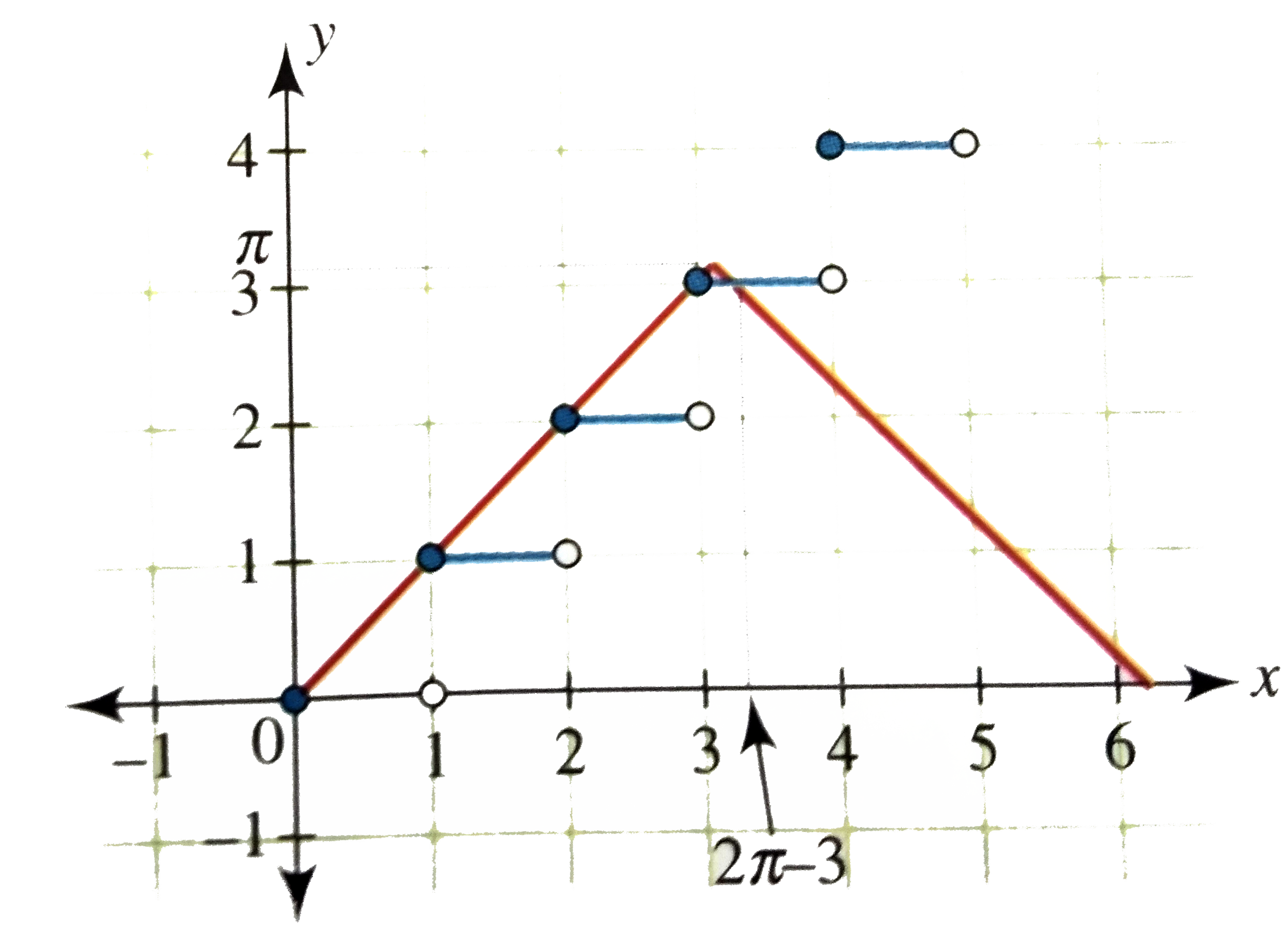 From the graph, roots are 0, 1, 2, 3, and the value OT x for which `3=2pi-x or x= 2 pi-3`. Hence the sum of roots is `2pi+3` |
|
| 5676. |
Evaluate the definite integrals . underset(0)overset(pi)int sqrt(2+2cos theta )d theta |
|
Answer» |
|
| 5677. |
Statement - 1 Let ABCD and BEFG are two parallelograms such that E lies on AD and C lies on FG then (ar (ABCD))/(ar(BEFG)) = 1 Statement - 2, ar(ABCD) = (1)/(2) ar (Delta BEC) = ar (BEFG) |
|
Answer» Statement - 1 is True, statement -2 is true, statement-2 is a CORRECT explanation FRO statement - 1 |
|
| 5678. |
Prove that A unit matrix is its own inverse. Is the converse true?If A= [[0,1,-1],[4,-3,4],[3,-3,4]]show thatA^2=I and hence A=A^(-1). |
|
Answer» Solution :No the converse is not TRUE for EXAMPLE:`A=`[[4,-1],[15,-4]]` `A^(-1)=-[[-4,1],[-15,-4]]=[[4,-1],[15,-4]]=A` |
|
| 5679. |
A pointp(x, y) moves in xy plane in such a way thatsqrt(2)le |x+y|+|x-y|le 2 sqrt(2). Area of the region representing all possible positions of the point 'p' is equal to : |
|
Answer» 2 SQ. UNITS |
|
| 5680. |
If inte^(x)/(x^(n))dx and -e^(x)/(k_(1)x^(n-1))+1/(k_(2)-1)I_(n-1), then (k_(2)-k_(1)) is equal to: |
|
Answer» 0 |
|
| 5682. |
A box contains 5 red balls , 6 green balls and 7 white balls. If three balls are drawn at random, then find the probability that these are green, red and white in the order if the balls are replaced. |
|
Answer» |
|
| 5683. |
An open box is to be made out of a piece of cardboard measuring (24cmxx24cm)by cutting off equal squares from the |
|
Answer» |
|
| 5684. |
If the primitive of (1)/(e^(x)-1)^(2) is f(x) - log |g (x)| + C then |
| Answer» Answer :C | |
| 5685. |
Find the transpose of each of the following matrices: (i)[(5),((1)/(2)),(-1)] (ii) [(1,-1),(2,3)] (iii) [(-1,5,6),(sqrt(3),5,6),(2,3,-1)] |
|
Answer» |
|
| 5687. |
For the system of circles given by (x^(2)+y^(2)+2gx)+lambda(x^(2)+y^(2)+2fy+l)=0, "where " g ne 0, f ne 0 " and " lamda is a parameter, if the line joining the points circles of the system subtends a right angle at the origin, thenk/f^(2)= |
|
Answer» -1 |
|
| 5689. |
Evaluate the following define integrals as limit of sums : lim_(n rarr oo) (1^(4)+2^(4) +3^(4) +....+n^(4))/(n^(5)) |
|
Answer» |
|
| 5690. |
Each question in this section has four choices A , B, C , and D out of which only one is coR Rect. Mark your choices as follows . LetR R be a real line, Consider the following subsets of the plane R R xx R R : S= {(x,y) : y =x+1 and 0 lt x lt 2 } T ={ (x,y) : (x-y) is an integer}. Statement - I : T is anequivalence relation on R R nut S is not an equivalence relation on R R. Statement -II : S is neither reflexive nor symmetric but T is reflexive symmetric and transitive. |
|
Answer» Statement -I is TRUE Statemint- IIis True, Statement -II is a CAR RECT explanation for Statement -I |
|
| 5691. |
Sixteen players S_(1),S_(2),…..S_(16) play in a tournament. They are divided into eight pairs at random from each pair a winner is decided on the basis of a game played between the two players of the pair. Assume that all the players are of equal strength. (i) Find the probability that the player S_(1) is among the eight winners. (ii) Find the probability that exactly one of the two playersS_(1) and S_(2) is among the eight winners. |
|
Answer» <P> `=("Probability of"S_(1) "being a pair")` `xx` (Prbability f `S_(1)` winnig the GROUP) `=1xx(1)/(2)=(1)/(2)""["since " S_(1) " is definitely in a group" ]` (ii)If `S_(1)and S_(2)` are in two separately, then exactly one wins. IF `S_(1)and S_(2)` will be among the eight winners. IF `S_(1)` wins and `S_(2)` loses or `S_(1)` losses and `S_(2)` wins. Now, the prbability of `S_(1).S_(2)` being the same pair and one wins `=("Probability of " S_(1),S_(2)` " being in the same pair" )` `xx` (Probability of anyone winning in the pair). and the probability of `S_(1),S_(2)` being thesame pair `=(N(E))/(n(S))` where, `n(E)=` the number of ways in which 16persons can be divided in 8 pairs. `therefore n(E)=((14)!)/((2!)^(7)*7!)and n(S)=((16)!)/((2!)^(8)*8!)` `therefore` Probability of `S_(1) and S_(2)` being in the same pair `=((14)!*(2!)^(8)*8!)/((2!)^(7)*7!*(16)!)=(1)/(15)` The probability of any one wining in the pairs of `S_(1),S_(2)=P` (certain event)= 1 `therefore` Thepairs of `S_(1),S_(2)` being in two pairs separately and `S_(1)` wins, `S_(2)` losses + The probability of `S_(1),S_(2)` being in two pairs separately and `S_(1)` loses , `S_(2)` wins. `=[1-((((14)!)/((2!)^(7)*7!))/(((16)!)))/((2!)^(8)*8!)]xx(1)/(2)xx(1)/(2)+[1-((((14)!)/((2!)^(7)*7!))/(((16)!)))/((2!)^(8)*8!)]xx(1)/(2)xx(1)/(2)` `=(1)/(2)xx(14xx(14)!)/(15xx(14)!)=(7)/(15)` `therefore` Required probability `=(1)/(15)+(7)/(15)=(8)/(15)` |
|
| 5692. |
By using the properties of definite integrals, evaluate the integrals int_((-pi)/2)^(pi/2)sinxdx |
| Answer» | |
| 5693. |
Prove that 2 tan^(-1)(1/2) + tan^(-1)(1/7) = tan^(-1)(31/17) |
Answer» SOLUTION : L.H.S =`TAN^(-1)((2xx1/2)/(1-(1/2)^2)) + tan^(-1)(1/7)` `= tan(1/(1-1/4)) + tan^(-1)(1/7) = tan^(-1)(4/3) + tan(1/7)` ` - tan^(-1)((4/3 + 1/7)/(1-4/3xx1/7)) = tan^(-1)((31/21)/(17/21)) - tan^(-1) (31/17)` = R.H.S |
|
| 5694. |
Equation ofnormal to x^(2)-4y^(2)=5 at theta=45^(@) is |
|
Answer» `2sqrt2x+2y=5sqrt5` |
|
| 5695. |
Two balls are drawn at random with replacement from a box containing 10 black and 8 red balls.Find the probability that i. both balls are red. ii. first ball is black and second is red. iii. one of them black and other is red: |
|
Answer» |
|
| 5696. |
If 'a' is the point of discontinuity of the function f(x)={(cos 2x",","for "-oo lt x lt 0),(e^(3x)",","for "0 le x lt 3),(x^(2)-4x+3",","for "3 le x le 6),((log(15x-89))/(x-6)",","for "x gt 6):} Then, lim_(x rarr a) (x^(2)-9)/(x^(3)-5x^(2)+9x-9)= |
|
Answer» 1 |
|
| 5697. |
If x gt 0 then int ("tan"^(-1) (x)/(x^(2) + 1) + "tan"^(-1) " "(x^(2) +1)/(x) )dx = |
|
Answer» `(X)/(2) + C ` |
|
| 5698. |
Three non zero numbers a, b, c are in A.P. Increasing a by 1 or increasing c by 2, the number become in G.P then b equals |
|
Answer» 10 |
|
| 5699. |
The orthocentre of the triangle whose vertices are (5,-2), (-1, 2) and (1,4) is |
|
Answer» `((1)/(5), (14)/(5))` |
|
| 5700. |
Using integration, find the area enclosed between the curve y=2x-x^(2), and the x-axis. |
|
Answer» |
|