InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 5601. |
If 1,alpha,alpha^(2),.......,alpha^(n-1) are the n^(th) roots of unity, then sum_(i=1)^(n-1)(1)/(2-alpha^(i)) is equal to: |
|
Answer» `((N-2)2^(n-1)+1)/(2^(n)-1)` |
|
| 5602. |
If displacement s, time t are related by s=sqrt(t) then I : Acceleration is proportional to velocity. II : Velocity is inverslyproportional to displacement. |
|
Answer» only I is TRUE |
|
| 5603. |
If1 , omega , omega^(2)are the cube roots of unity prove that (a + b) ( a omega + b omega^(2))(aomega^(2) + b omega) = a^(3) + b^(3) |
| Answer» | |
| 5604. |
A square is inscribed in the circel x^(2)+y^(2)-2x+7y-8=0 whose diagonals are parallel to axes and a vertex in the firstquadrant is A then OA is |
| Answer» Answer :B | |
| 5605. |
Consider the matrix A=[(4,1),(1,5)] on applying elementary row operations R_(2)toR_(3)-n_(1), it becomes [(4,3),(-11,-4)], then the value of n= |
|
Answer» 2 |
|
| 5606. |
Ifalpha=2vec(i) +3vec(j) -5vec(k) and beta= vec(i)-vec(j) , then find the value of alpha xx beta |
| Answer» | |
| 5607. |
Obtain the following integrals : int(x^(2))/(1-x^(4))dx |
|
Answer» |
|
| 5608. |
The slope of a line is 3 times the slope of the other line and the tangent of the angle between them is 4/13, sum of their slopes is equal to |
|
Answer» 2 |
|
| 5609. |
If f(x) = {(-2sinx,for xle -pi/2)(asinx+b,for -pi/2ltxltpi/2)(cosx,for xgepi/2):} everywhere then the ordered pair(a,b) is |
|
Answer» (-1,1) |
|
| 5610. |
Simplify tan^(-1)[(a cos x -b sin x)/(b cos x +a sin x)] if a/b tan x gt -1 |
|
Answer» |
|
| 5612. |
State with reason, "Collection of all winged horses " is set or not ? |
| Answer» SOLUTION :It is a SET, as it is PROPERLY DEFINED. | |
| 5613. |
The loucs of the midpoints of the chords of the circle 4x^(2)+4y^(2)-12x+4y+1=0 which subtend an angle of pi//3 as its centre is a circle of radius |
|
Answer» `3/4` |
|
| 5614. |
A beam of 5 ke V alpha-particlesand a beam of 5 ke V electronsare absorbed by a target. The two beams deliver equal amountsof energy to the target per second. If ("mass of "alpha-"particle")/("mass of electron")=7.27xx10^(3), what is the value of ("pressure on target due to "alpha - "particle")/("pressure on target due to electron")? |
|
Answer» `1.38xx10^(-4)` then rate of energy transfer `=nxx(1)/(2)MV^(2)=n(K.E.)` SINCE Rate of momentum transfer `=nxxmv=nxxsqrt(2m(KE))` Since both beam transfer equal energy, `n_(1)(KE)_(1)=n_(2)(KE)_(2)`, but `KE_(1)=KE_(2)rArr n_(1)=n_(2)` `:.` RATIO of momentum transferred `=(n_(1)sqrt(2m_(1)(KE)_(1)))/(n_(2)sqrt(2m_(2)(KE)_(2)))=(sqrt(m_(1)))/(sqrt(m_(2)))=sqrt(7270)` |
|
| 5615. |
A circle passes through origin and meets the axes at A and B so that (2,3) lies on bar(AB) then the locus of centroid of DeltaOAB is |
|
Answer» `2x-3y=6xy` |
|
| 5616. |
Statement 1: An equation of a common tangent to the parabola y^(2) =16 sqrt3 xand the ellipse2x^(2) +y^(2) =4isy= 2x +2sqrt3.Statement 2: If the line y= mx+ ( 4sqrt3)/( m ) , (m ne 0) is a common tangent to the parabolay^(2)= 16 sqrt3x and the ellipse 2x^(2) +y^(2) =4,then m satisfiesm^(4) +2m^(2) =24. |
|
Answer» Both the STATEMENT are True and statement 2 is the correct EXPLANATION of statement 1 |
|
| 5617. |
Position of a particle moving in straight line is x=t^3-3t^2.If average speed of particle in interval 0-4 sec is 'a' and average velocity in same period is 'b'. Then what is the value of a/b. |
|
Answer» |
|
| 5618. |
A cone with its height equal to the diameter of the base is expanding in volume at the rate of 50 cm^(3)//sec. If the base has area 1 m^(2) , the radius is increasing at the rate ………. |
|
Answer» 0.0025 cm/sec |
|
| 5619. |
If f(x)= |sin x|, then |
|
Answer» F is everywhere differentiable |
|
| 5620. |
The solution of the differential equation y' = (1)/(e^(-y) - x) is |
|
Answer» `X = E^(-y) (y + C)` |
|
| 5622. |
int_(-pi)^(pi) (2x(1+Sin x))/(1+Cos^(2)x)dx= |
|
Answer» `PI^(2)` |
|
| 5623. |
Absorption of water, simple sugar and alcohol take place in :- |
| Answer» Answer :A | |
| 5624. |
Find a unit vector perpendicular to each of the vector veca+vecbandveca=3hati+2hatj+2hatkandvecb=hati+2hatj-2hatk. |
|
Answer» |
|
| 5625. |
8n players P_(1),P_(2),P_(3),....,P_(8n) play a knock out tournament. It is known that all the players are of equal strngth. The tournat random is held in three rounds where the players are paired at random in each rouns. If it is given that P_(1) wins in the third round. Find the probability than P_(2)loses in the second round. |
|
Answer» SOLUTION :Let A be the EVENT of `P_(1)` winning in third round and B be the event of `P_(2)` winning in first round but ossing in second round. We have `P(A)(""^(8n-1)C_(n-1))/(""^(8n)C_(n))=1/8` `P(BnnA)` = Probability of both `P_(1) and P_(2)`winning in first round `xx` Probability of `P_(1)` winning and `P_(2)` losing in second round `xx` probability of `P_(1)` winning in third round `(""^(8n-2)C_(4n-2))/(""^(8n)4_(n))xx(""^(4n-2)C_(2N-1))/(""^(4n)C_(2n))xx(""^(2n-1)C_(n-1))/(""^(2n)C_(n))=(n)/(4(8n-1))` Hence, `P((B)/(A))=(P(BnnA))/(P(A))=(2n)/(8n-1)` Alternate solution: Probability than `P_(2)` wins in first round GIVEN `P_(1)` wins is `P((B)/(A))=(P(BnnA))/(P(A))=(2n)/(8n-1)` In second round, probability that `P_(2)` loses in second round given `P_(1)` wins in `1-(2n-1)/(4n-1)=(2n)/(4n-1)` Hence, probability than `P_(2)` loses in second round, given `P_(1)` wins in third round is 2n/(8n-1). |
|
| 5626. |
Find the equation of the circle passing through the origin and having the centre at (-4,3) |
|
Answer» |
|
| 5627. |
int(x+sqrt(x^(2)+1))^(n)dx |
|
Answer» |
|
| 5628. |
Let S = {x in R : sqrt(x^(2) + 19 x ) - sqrt(x) + sqrt(x + 19) = x + 6 . 08} , "then" sum_(x in S) x = ________ |
|
Answer» |
|
| 5629. |
Evaluate the following definite integrals . int_(0)^(4)(x+e^(2x))dx |
|
Answer» |
|
| 5630. |
A telephone exchange receives on an average 180 calls per hour. Find the probability that it will receive only 2 calls in a given minute. |
|
Answer» |
|
| 5631. |
From a point A(1,0) on the circle x^(2) + y^(2) - 2x + 2y + 1 =0, a chord AB is drawn and it is extended to a point P such that AP = 3AB. The equation of the locus of P is |
|
Answer» `x^(2) + y^(2) -2X + 6y + 1=0` |
|
| 5632. |
If nsinx=log_(e)x has exactly 1 root, then find the possible value of n(ninN). |
|
Answer» Solution :`nsinx=log_(e)x` `impliessinx=(log_(e)x)/(n)` For exactly one root, the graph of `y=sinx` must intersect the graph of `y=(log_(e)x)/(n)` exactly once. Maximum value of sin x is 1. 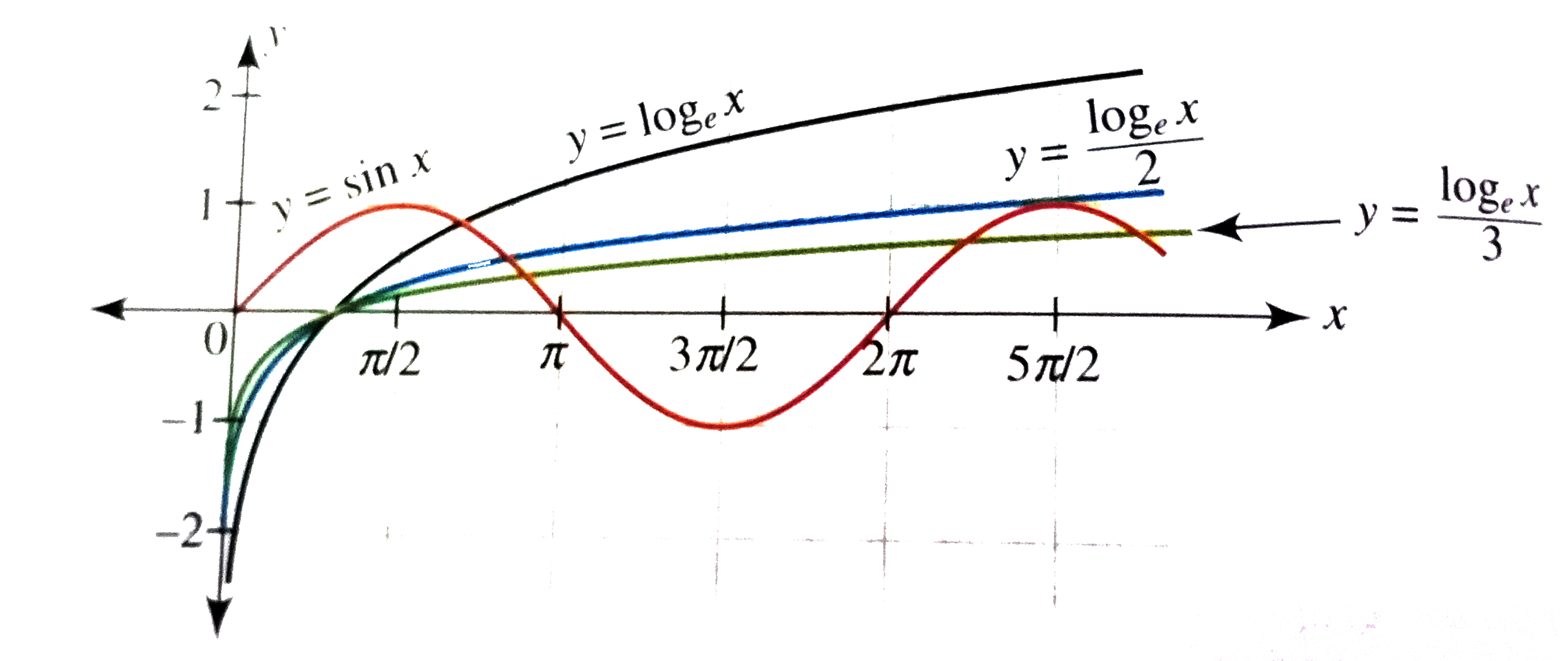 For `n=1,sinx=log_(e)x` Graphs of `y=sinxandy=log_(e)x` intersect only once as shown in the FOLLOWING figure. For `x=e,log_(e)e=1`, hence after `x=e,y=log_(e)x` never meets `y=sinx`. For `n=2,"let"(log_(e)x)/(2)=1:.log_(e)x=2orx=e^(2)lt5pi//2` Hence the graph of `y=(log_(e)x)/(2)` meets `y=sinx` only once. But for `n=3and(log_(e)x)/(3)=1,x=e^(2)gt5pi//2` hence the graph of `y=(log_(e)x)/(3)` MEET the graph of `y=sinx` more than once. So for exactlly one root of the EQUATION `sinx=(log_(e)x)/(n),n=1or2`. |
|
| 5633. |
Find the number of ways of arranging the letters of the word SPECIFIC. In how many of them the two C's come together |
|
Answer» |
|
| 5634. |
The sequences {x_(n)}is definedby x_(k+1)=x_(k)^(2)+x_(k) and x_(1) =1/2Let S = [ 1/(x_(1)+1)+1/(x_(2)+1)+...+1/(x_(m)+1)] ( where [.] denotes the freatest integar function ) |
|
Answer» S=0 , if m = 40 |
|
| 5635. |
(1-1/(1!) +9/(2!) +(27)/(3!) + .....oo) (1+9/(1!) +(81)/(2!)+(729)/(3!)+ .....oo)= |
|
Answer» 1 |
|
| 5636. |
Vapour density of an ideal gas which has a density 2.16 g//L at 1.12 atm pressure & 273 K temperature (R=0.0821) |
|
Answer» |
|
| 5638. |
Determine 'a' such that x^2 - 11x + a and x^2 - 14x + 2a may have a common factor. |
|
Answer» |
|
| 5639. |
Show that every polynomial function is continuous. |
|
Answer» <P> |
|
| 5640. |
Find the equation of lines joining the points. (a,a,a) and (a,0,a) |
| Answer» SOLUTION :EQUATION of the line joining the points (a,a,a) and (a,0,a) is `(x-a)/(a-a)=(y-a)/(0-a)=(z-a)/(a-a)` or `(x-a)/0=(y-a)/(-a)=(z-a)/0` | |
| 5641. |
Find the conditions that the tangents drawn from the exteriorpoint (g,f)toS= x^(2) + y ^(2) + 2gx + 2fy + c=0are perpendicular to each other. |
|
Answer» |
|
| 5642. |
If underset(x to 0)lim (x^(-3) sin 3x+ax^(-2) +b) exists and is equal to 0, then |
|
Answer» a=-3 and b=9/2 |
|
| 5643. |
If U_(n)=int_(0)^(pi)(1-cosnx)/(1-cosx)dx where n is positive integer of zero, then The value of U_(n) is |
|
Answer» `pi//2` `=int_(0)^(pi)(cos(n+1)x-cos(n+2)x)/(1-cosx)` `=int_(0)^(x)(2sin(n+3/2)x . "SIN"x/2)/(2sin^(2)x//2)dx` `implies U_(n+2)-U_(n+1)=int_(0)^(pi)("sin"(n+3/2)x)/("sin"x/2)dx`.................1 `impliesU_(n+1)-U_(n)=int_(0)^(pi)("sin"(n+1/2)x)/("sin"x/2)dx`.............2 From 1 and 2 we get `(U_(n+2)-U_(n-1))-(U_(n+1)-U_(n))` `=int_(0)^(pi)(sin(n+3/2)x-sin(n+1/2)x)/("sin"x/2)dx` `implies U_(n+2)+U_(n)-2U_(n+1)` `=int(2cos(n+1)x.sinx//2)/(sinx//2) dx` `=2int_(0)^(pi)cos(n+1)x dx` `=2((sin(n+1)x)/(n+1))-(0)^(pi)=0` `impliesU_(n+2)+U_(n)=2U_(n+1)` `implies U_(n),U_(n+1),U_(n+2)` are in A.P. `U_(0)=int_(0)^(pi)(1-1)/(1-cosx)dx=0` `U_(1)=int_(0)^(pi)(1-cosx)/(1-cosx) dx=pi` `U_(1)=U_(0)=pi` (common difference) `:.U_(n)=U_(0)+npi=npi` Now, `I_(n)=int_(0)^(pi//2) (sin^(2) n THETA)/(sin^(2) theta) d theta` `=int_(0)^(pi//2) (sin^(2) n theta)/(sin^(2)theta) d theta` `=int_(0)^(pi//2) (1-cos2 n theta)/(1-cos 2THETA) d theta=1/2 int_(0)^(pi)(1-cosn x)/(1-cosx) dx` `impliesI_(n)=1/2npi` |
|
| 5644. |
Draw the graph of y=tan^(-1)((2x)/(1-x^(2))) |
|
Answer» Solution :We have `y=f(x)=tan^(-1)((2x)/(1-x^(2)))` Domain of f(x) is R-{-1, 1}. Let `x=tantheta in (-PI//2,pi//2)` `rArr""theta=tan^(-1)x` `"Now"tan^(-1)((2x)/(1-x^(2)))=tan^(-1)((2tantheta)/(1-tan^(2)theta))` `=tan^(-1)(tan2theta)` `=tan^(-1)(tanalpha)" where "alpha in (-pi, pi)` Now consider the graph of `y=tan^(-1)(tan alpha)," where "alpha in (-pi, pi)`. 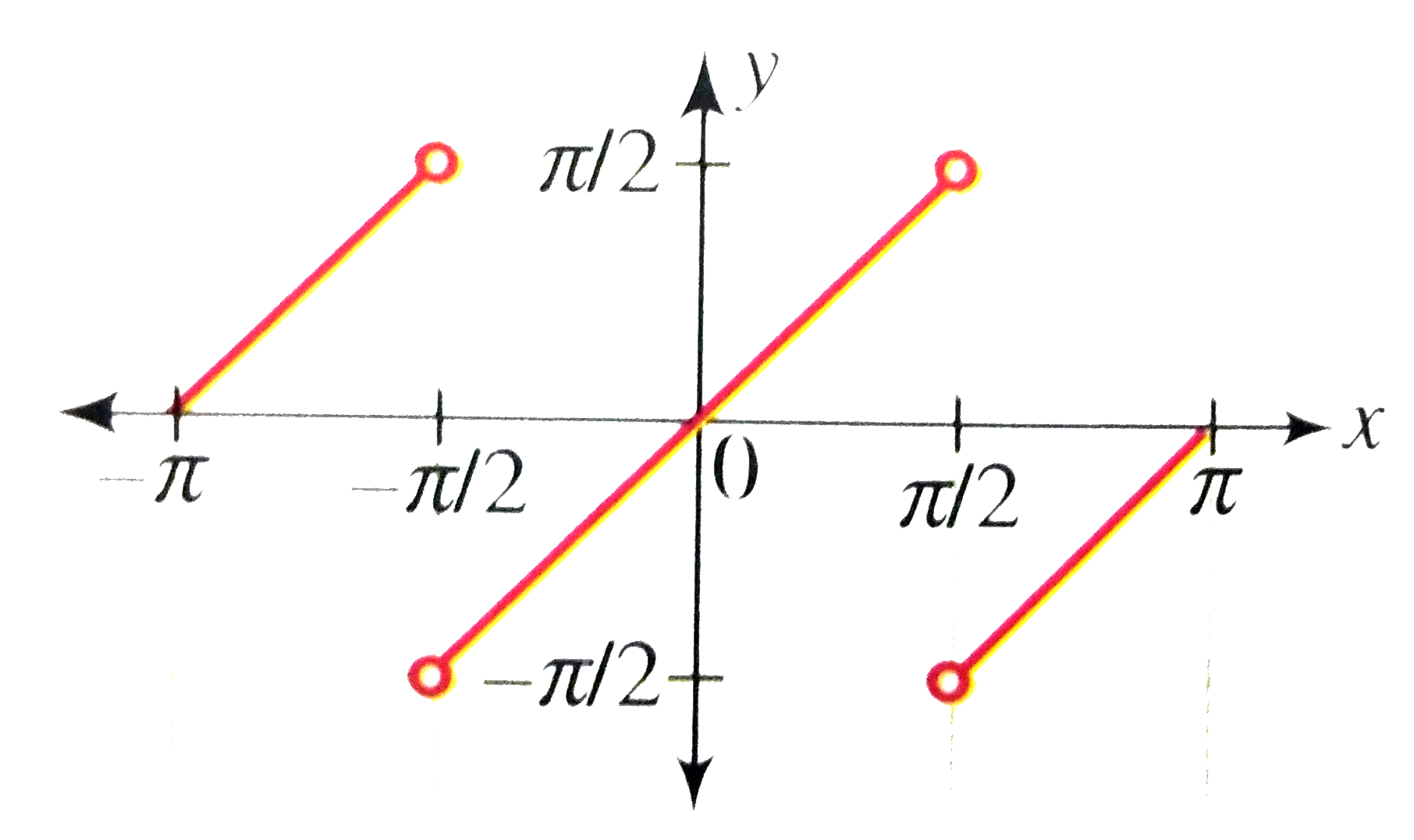 Form the graph, `tan^(-1)((2x)/(1-x^(2)))=tan^(-1)(tan alpha)` `={{:(alpha+pi,-piltalphalt-pi//2),(alpha, -pi//2ltalphaltpi//2),(alpha-pi,pi//2lealphaltpi):}` `={{:(2tan^(-1)x+pi,-pilttan^(-1)xlt-pi//2),(2tan^(-1)x, -pi//2lttan^(-1)xltpi//2),(2tan^(-1)x-pi,pi//2lt2tan^(-1)xltpi):}` `={{:(2tan^(-1)x+pi,-pilttan^(-1)xlt-pi//4),(2tan^(-1)x, -pi//4lttan^(-1)xltpi//4),(2tan^(-1)x-pi,pi//4lt2tan^(-1)xltpi//2):}` `={{:(2tan^(-1)x+pi, -ooltxlt-1),(2tan^(-1)x,-1ltxlt1),(1tan^(-1)x-pi,1ltxltoo):}` `tan^(-1)" is an increasing FUNCTION for "x in R`. THUS, all branch functions in the above are increasing functions. `underset(xto-oo)(lim)(tan^(-1)x+pi)=0,underset(xto-1)(lim)(2 tan^(-1)x+pi)=pi/2` Thus, `tan^(-1)((2x)/(1-x^(2)))` increases form 0 to `pi/2` when x increases from `-oo" to "-1` `underset(xto-1)(lim)(2tan^(-1)x)=pi/2, underset(xto1)(lim)(2 lim^(-1)x)-pi/2" and "2 tan^(-1)0=0` Thus, `tan^(-1)((2x)/(1-x^(2)))" increases form "-pi/2" to "pi/2" when x increases from -1 to 1, intersecting the x-axis at x=0"`. `underset(xto1)(lim)(2tan^(-1)x-[pi)=-pi/2,underset(xtooo)(lim)(2tan^(-1)x-pi)=0` Thus, `tan^(-1)((2x)/(1-x^(2)))" increases form "-pi/2" to0 when x increases from 1 to "oo.` From this information, we can draw the graph of `y=tan^(-1)((2x)/(1-x^(2)))` as folows. 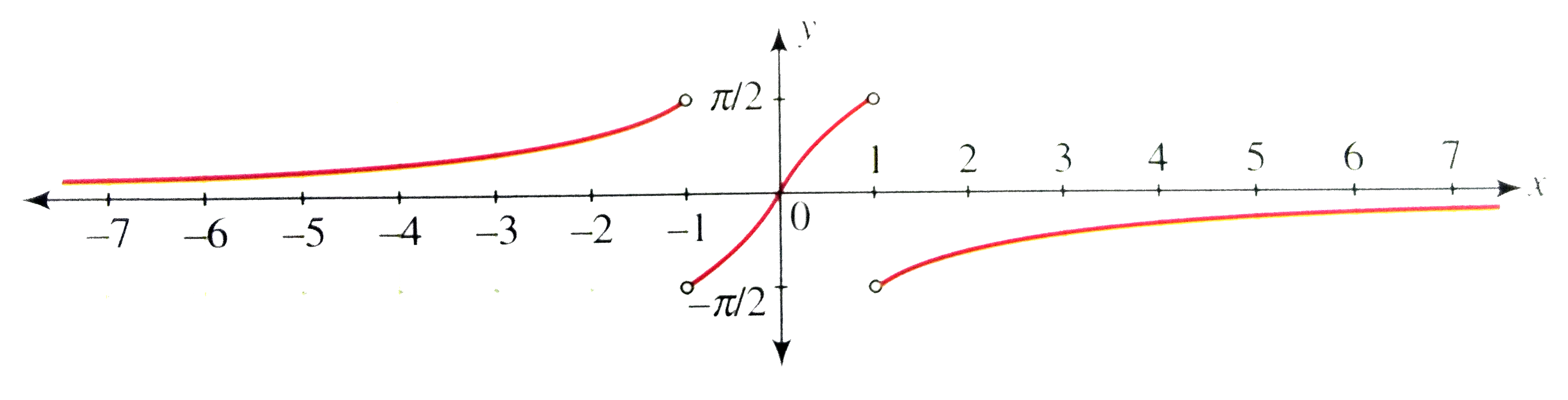 Here y = 0 is na anymptote. |
|
| 5645. |
Evaluate the following integrals. int(1)/(sqrt(x^(2)+2x+3))dx |
|
Answer» |
|
| 5646. |
A unit vector perpendicular to each of the vectors 2hat(i)-hat(j)+hat(k)and 3hat(i)-4hat(j)-hat(k) is |
|
Answer» `(1)/(sqrt(3))hat(i)+(1)/(sqrt(3))hat(J)-(1)/(sqrt(3))hat(K)` `=hat(i)(1+4)-hat(j)(-2-3)+hat(k)(-8+3)` `=5hat(i)+5hat(j)-5hat(k)` Unit vector `=(5)/(5sqrt(3))hat(i)+(5)/(5sqrt(3))hat(j)-(5)/(5sqrt(3))hat(k)` `=(1)/(sqrt(3))hat(i)+(1)/(sqrt(3))hat(j)-(1)/(3sqrt(3))hat(k)` |
|
| 5647. |
Find the coordinates of the centre of gravity of the catenary y=(1)/(2) (e^(x) + e^(-x))= cos h x between A(0, 1) and B(a, cosh a). |
|
Answer» |
|
| 5648. |
Equation of a circle with centre (-4,3) touching internally and containing the circle x ^(2) + y ^(2) =1 is |
|
Answer» `X ^(2) + y^(2) + 8X-6Y + 9=0` |
|
| 5649. |
The middle term in the expansion of (x/3-2/sqrt(x))^(6) is |
|
Answer» `(-160)/27X^(3/2)` |
|
| 5650. |
Write the equation of the plane passing through the point (2, 3, 1) andperpendicular to the line.(x-1)/1=(y-2)/-1=(z+1)/3 |
| Answer» Solution :In the GENERAL EQUATION of a plane there are 3 INDEPENDENT CONSTANTS. | |