InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 11951. |
If the volume of the parallelepiped formed by three non-coplanar vectors vec(a),vec(b)andvec(c) is 4 cubic units, then [vec(a)xxvec(b).vec(b)xxvec(c).vec(c)xxvec(a)]= |
|
Answer» 8 |
|
| 11952. |
int(dx)/(2+cosx-sinx)= |
|
Answer» `sqrt(2)tan^(-1)((1)/(2)(tan((x)/(2))-1))+c` |
|
| 11953. |
A biased coin with probability p(0ltplt1) of getting heads, is tossed until a head appears for the first time. If the probability that the number of tosses required is even is 1//5, then p is equal to……. |
|
Answer» `(2)/(3)` BREAK into PARTIAL fractions. |
|
| 11954. |
|(b^(3)+c^(2),ab,ac),(ab,c^(2)+a^(2),bc),(ca,bc,a^(3)+b^(2))|= |
|
Answer» `2A^(3)b^(2)C^(2)` |
|
| 11955. |
Draw the graph of y=sin^(-1)((2x)/(1+x^(2))) |
|
Answer» Solution :We have `y=f(x)=sin^(-1)((2x)/(1-x^(2)))` LET x `=tan, theta, theta in (-pi//2,pi//2)` `rArr""theta=tan^(-1)x` `"Now"sin^(-1)((2x)/(1+x^(2)))=sin^(-1)((2tantheta)/(1+tan^(2)theta))` `=sin^(-1)(sin2theta)` `=sin^(-1)(sinalpha), "where "alpha in (-pi, pi)` Now consider the graph of `y=sin^(-1)(sin alpha),"where "alpha in (-pi, pi)` 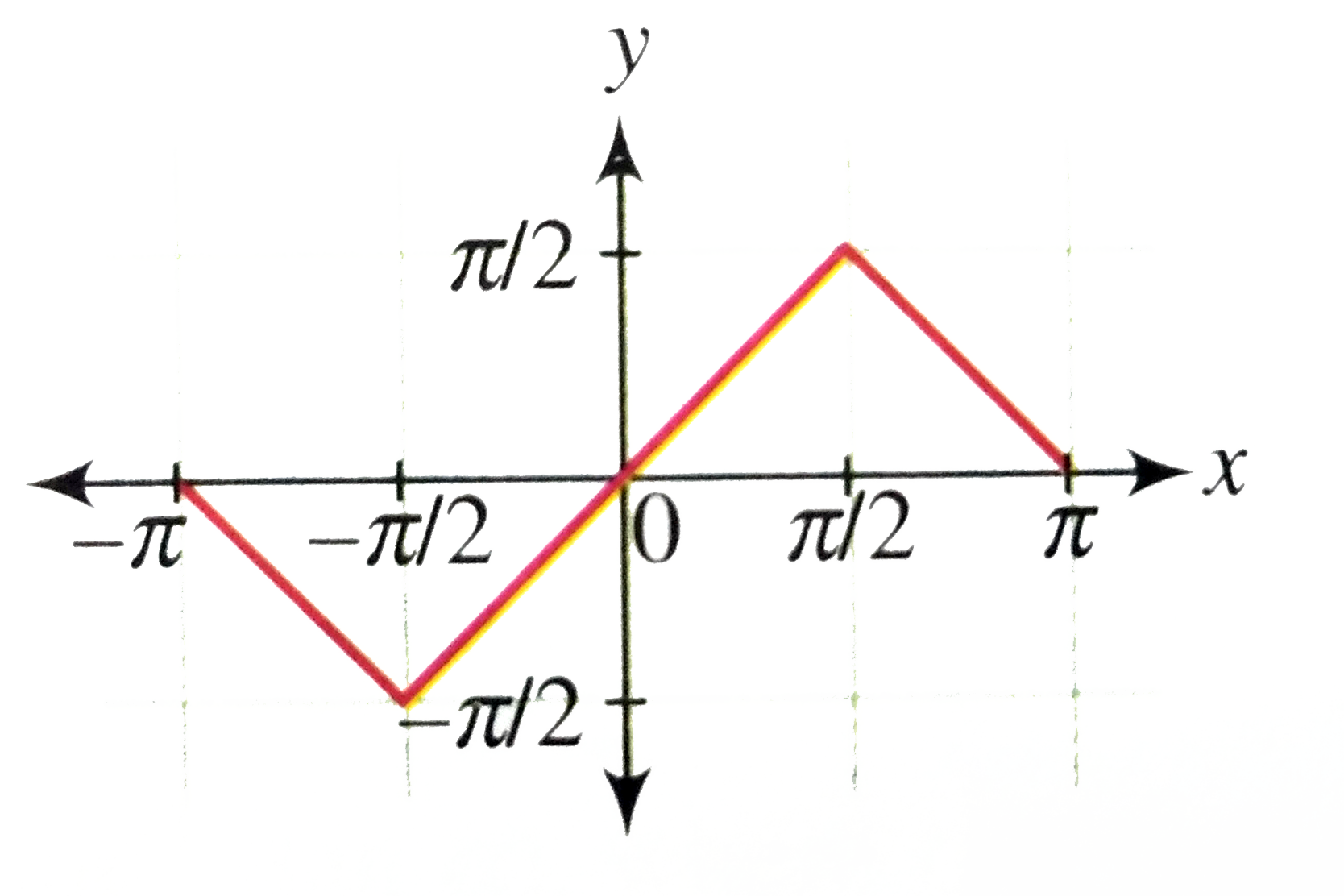 From the graph. `sin^(-1)((2x)/(1+x^(2)))=sin^(-1)(sinalpha)` `={{:(-alpha-pi, -piltalphalt-pi//2),(alpha, -pi//2lealphalepi//2),(-alpha+pi,pi//2ltalphaltpi):}` `={{:(-2tan^(-1)x-pi,-pilt2tan^(-1)xlt-pi//2),(2tan^(-1)x-pi, -pi//2le2tan^(-1)xlepi//2),(-2tan^(-1)x+pi,-pi//2lttan^(-1)xltpi):}` `={{:(-2tan^(-1)x-pi,-pilt2tan^(-1)xlt-pi//4),(2tan^(-1)x-pi, -pi//2le2tan^(-1)xlepi//4),(-2tan^(-1)x+pi,-pi//4lttan^(-1)xltpi//2):}` `={{:(-2tan^(-1)x-pi,xlt-1),(2tan^(-1)x, -1lexle1),(-2tan^(-1)x+pi,xgt1):}` `f(x)={{:(-2/(1+x^(2)),xlt-1),(2/(1+x^(2)),-1ltxlt1),(-2/(1+x^(2)),xgt1):}` So f(x) DECREASES for `xlt-1xgt" and f(x) INCREASES for"-1ltxlt1` `underset(xto-oo)(lim)(-2tan^(-1)x-pi)=0" and "-2tan^(-1)(-1)-pi-pi/2` Thus, `sin^(-1)((2x)/(1+x^(2)))"decreses form 0 to"-pi/2"when x increases form "-oo" to "-1` `f(-1)=2tan^(-1)-pi/2,f(1)=2tan^(-1)(1)=pi/2` Thus, `sin^(-1)((2x)/(1+x^(2)))" increases form "-pi/2" to "pi/2" when x increases form -1 to 1"` `-2tan^(-1)(1)+pi=pi/2" and"underset(xtooo)(lim)(-2tan^(-1)x+pi)=0` Thus, `sin^(-1)((2x)/(1+x^(2)))"decreases form "pi/2" to 0 when x increases form 1 to "oo`. Also f(x) is non-differentiable at `x=+-1` From the above information, the graph of `y=f(X) ` is as SHOWN in the following figure. 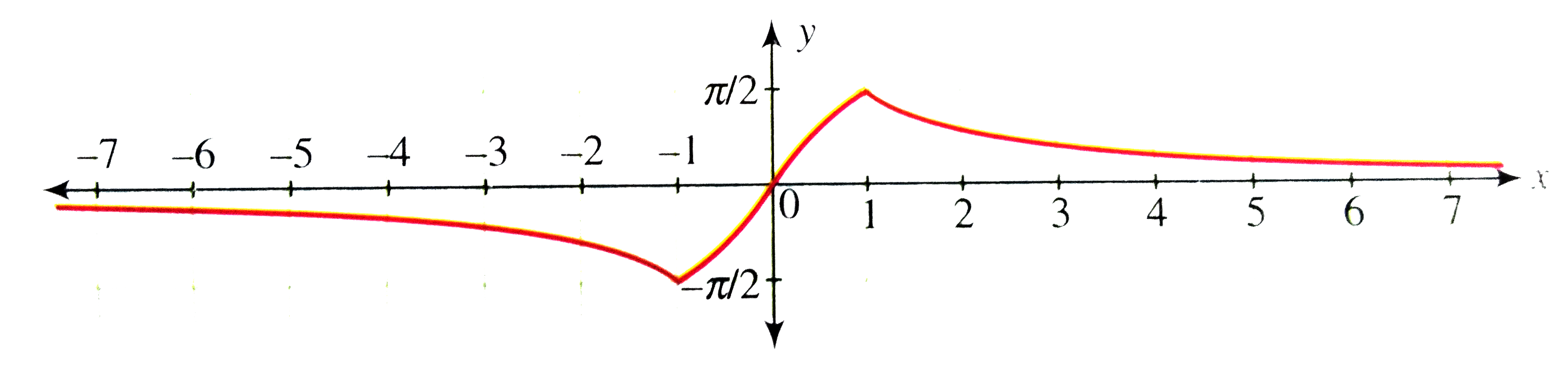 From this information, we can DRAW the graph of `y=sin^(-1)((2x)/(1+x^(2)))` as follows. Here y = 0 is an asymtote. |
|
| 11956. |
Find the number of on-to functions from a set A onto B where n(A)=6 and n(B)=4. |
|
Answer» |
|
| 11957. |
A(3,-1),B(2,3) and C(5,1) are given then m angleA = ……… |
|
Answer» `cos^(-1)""(3)/(sqrt(34))` |
|
| 11958. |
By using the properties of definite integrals evaluate the integrals in exercise. overset((pi)/(2)) underset(0)int (sqrt(sinx))/((sqrt(sinx)+ sqrt(cosx)))dx |
|
Answer» |
|
| 11959. |
By using the properties of definite integrals evaluate the integrals in exercise. overset((pi)/(2)) underset(0)int cos^(2)x dx |
|
Answer» |
|
| 11960. |
By using the properties of definite integrals evaluate the integrals in exercise. overset((pi)/(2)) underset(0) int (cos^(5)x)/(sin^(5)x+cos^(5)x)dx |
|
Answer» |
|
| 11961. |
If u,v,w are three nonceplannar vectors then (u + v - w), (u - v) xx (v - w) = |
|
Answer» 0 |
|
| 11962. |
You are given that A and B are two events such that P(B)= (3)/(5), P(A//B)= (1)/(2)and P(A cup B)= (4)/(5)then P(B//A') is equal to ……… |
| Answer» Answer :D | |
| 11963. |
Solvetheequation x^4 -5x^3 +4x^2 +8x -8=0giventhat1- sqrt(5) isa root |
|
Answer» |
|
| 11964. |
By using the properties of definite integrals evaluate the integrals in exercise. overset((pi)/(2)) underset(0) int (2 log sin x-log sin 2x)dx |
|
Answer» |
|
| 11965. |
Huey's Hip pizza sells two sizes of square pizzas a small pizza that measures 10 inches on a side and costs $10, and a large pizza that meausres 15 inches on a side and costs $20. If two friends go to Huey's with $30 apiece, how many more square inches of pizza can they buy it they pool their money than if they each purchase pizza alone? |
|
Answer» |
|
| 11966. |
int(cos 2x-cos 2 theta)/(cosx-cos theta)dx=....+C |
|
Answer» `2(sinx+x COS THETA)` |
|
| 11967. |
The value of int(dx)/(5+4cosx) is |
|
Answer» `(1)/(3)TAN^(-1)((1)/(3)tanx)+C` |
|
| 11968. |
Evaluate the following integrals. int(1)/(sqrt(2+x-3x^(2)))dx |
|
Answer» |
|
| 11969. |
int (cos 4x + 1)/(cot x - tan x) dx = |
|
Answer» `(1)/(8) COS 4x + C ` |
|
| 11970. |
Let E(n) denote the sum of the even digits of n. For example, E (1243)=2 +4 =6. What is the value of E(1) + E(2) + E(3)+…….+ E(100)? |
|
Answer» |
|
| 11971. |
If int(2cosx-sinx-1)/(cosx+sinx-2)dx=Blog|f(x)|+Dx+C then |f(0)| + B + 2D is equal to |
|
Answer» |
|
| 11972. |
State True or False .A function is not differentiable at x=crArrfis not continuous at x=c. |
|
Answer» |
|
| 11973. |
The projection of the vector hati+3hatj+7hatk on the vector 7hati-hatj+8hatk is |
|
Answer» `(60)/(sqrt(122))` ` (a.b) /(|b|)=[((hati +3hatj +7 hatk).(7 hati -hatj+8hatk))/(sqrt(7)^(2)+(-1)^(2)+8^(2))]` `=[(1xx7+3xx(-1)+7xx8)/((sqrt(49)+1+64))]=(7-3+56)/(sqrt(114))=(60)/(sqrt(114))` |
|
| 11975. |
int_(0)^(pi//4)[sqrt([1-sin2x)/(1+sin2x)]dx= |
|
Answer» `1/2 LN 2` |
|
| 11976. |
Statement 1 The tangent and normal at any point P on a ellipse bisect the external and internal angles between the focal distance of P. Statement 2 The straight line joining the foci of the ellipse subtends of a right angle at P. |
|
Answer» Statement I is true, statement II is true: statement II is a CORRECT explanation for statement I |
|
| 11977. |
If |bar(x)+bar(y)|=|bar(x)-bar(y)|, then |
|
Answer» `BAR(X)` is PARALLEL to `bar(y)` |
|
| 11978. |
The value of Deltalogf(x)+Delta^(2)(3^(x)) is |
|
Answer» `LOG[1+(Deltaf(x))/(F(x))]+4.3^(x)` `log f(x+h)-log f(x)+(E-)^(2)3^(x)` `=log [ (f(x+h))/(f(x))]+(E^(2)-2E+1)3^(x)` `=log [ (E(x+h))/(f(x))]+E^(2)(3^(x))-2E(3^(x))+3^(x)` `=log [ (E(x+h))/(f(x))]+E^(2)(3^(x))-2E(3^(x))+3^(x)` `=log[1+(Delta f(x))/(f(x))]+3^(x)(9-6+1)` `=log[1+(Delta f(x))/(f(x))]+4*e^(x)` |
|
| 11979. |
Find the vertex, focus, equation of directrix and axis, of parabolas y^(2) - 2y + 8x - 23 = 0 |
|
Answer» |
|
| 11980. |
A flag- staff 6 metre high is placed on the top of a tower . The flag-staff casts a shadow , which is 2sqrt3 metre long wen measured along the ground . The angle , in degrees , that the sun-rays make with the ground is |
|
Answer» `60^(@)` |
|
| 11981. |
On the sides AB,BC,CA of triangle AB, 3,4,5 distinct points (excluding vertices A, B, C) are respectively chosen. The number of triangles that can be constructed using these chosen points as vertices are |
|
Answer» 210 |
|
| 11982. |
Find (dy)/(dx) in the following : x^(2)+xy+y^(2)= 100 |
|
Answer» |
|
| 11983. |
sin h ^(-1) 2 + cos h ^(-1) 2- tanh ^(-1) ""(2)/(3) + cot h ^(-1) (2)= |
|
Answer» `LOG ((4 + 2SQRT3 +2 sqrt5+ sqrt15)/(sqrt15))` |
|
| 11984. |
Evaluate the following integrals (i) int_(0)^(pi/2) (sin^(2) x - cos^(2) x)/(sin^(3) x + cos^(3) x) dx |
|
Answer» 0 |
|
| 11985. |
The point A(-1,3,0), B(2,2,1) and C(1,1,3) determine a plane. The distance from the plane to the point D(5,7,8) is |
|
Answer» `SQRT(66)` |
|
| 11986. |
Find the probability distribution of the number of kings when 2 cards are drawn one by one without replacement from a pack of 52 playing cards, |
|
Answer» |
|
| 11987. |
IfP( 3 sec theta, 2 tan theta )and Q( 3sec phi, 2 tan phi ) " where" theta +phi =(pi )/(2) , be two distinct points on the hyperbola (x^(2))/( 9)-(y^(2))/( 4)=1 . Then the coordinate of the points of intersection of the normals at Pand Q is |
|
Answer» `(11)/(3) ` |
|
| 11988. |
Using the properties of determinants in Exercise 1 to 6, evaluate |{:(3x,-x+y,-x+z),(x-y,3y,z-y),(x-z,y-z,3z):}| |
|
Answer» |
|
| 11989. |
If "log"_(1//sqrt(2))|z+1|lt log_(1//sqrt(2))|z-1|,|z-2i|lt |z+2i| and log_(1//2)|omega-3i|gt log_(1//2)|omega+3i|,|omega+1|lt |oemga-1| then sin("arg"((z)/(omega))) is |
| Answer» Answer :C | |
| 11990. |
If a line makes angles alpha, beta, gamma when the positive direction of coordinates axes, then write the value of sin^(2) alpha + sin^(2) beta + sin^(2) gamma. |
|
Answer» 3 |
|
| 11992. |
Let S_(n) denote the sum of first n terms of an A.P. If S_(4) = -34,S_(3) = - 60 and S_(6) =- 93, then the common difference and the first term of the A.P. are respectively. |
| Answer» ANSWER :A | |
| 11993. |
int (cos^(3)x + cos^(5) x)/(sin^(2)x + sin^(4) x) dx = |
|
Answer» `SIN X- 6 tan^(-1) (sin x) + C` |
|
| 11994. |
Let R be the relation on the set N given by R= { (a, b): a= b-2, b gt 6}. Choose the correct answer. |
| Answer» Answer :A | |
| 11995. |
The length of tangent to the curve x=a(cost+log tan.(t)/(2)),y=a(sint), is |
|
Answer» |
|
| 11996. |
int sqrt(x^(2)+2x+5)dx is equal to |
|
Answer» 1.`(1)/(2)(x+1)SQRT(x^(2)+2x+5)+2 LOG|x+1+sqrt(x^(2)+2x+5)|+C` |
|
| 11997. |
If a, b, c are in A.P., b, c, d are in G.P. and 1/c,1/d,1/e are in A.P. prove that a,c,e are in GP. |
|
Answer» |
|
| 11998. |
int(dx)/((x-1)^(2)(x^(2) +1))= |
|
Answer» `log_(E) sqrt(X +1) +(1)/(2) log_(e)sqrt(x^(2) +1) - (1)/(x +1)+C` |
|
| 11999. |
Simplify the following (sqrt(3)+1)^(5) -(sqrt(3) -1)^(5) |
|
Answer» |
|
| 12000. |
Five boys and four girls randomly stand in a line. Find the probability that no two girls come together. |
|
Answer» Solution :Five BODY and 4 girl randomly stand in a LINE such that no two girls come together. `therefore absS=9 |`  The 4 girls can stand in 6 positions in `^6P_4` ways. Further 5 body can stand in 5 ! ways. The 4 girls can stand in 6 positions in `^6P_4` ways. Further 5 body can stand in 5 ! ways. `therefore` PROBABILITY that they will stand in a line such that no two girls come together. `=(51xx"^6P_4)/91=5/42` |
|