InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 12051. |
If A is a 3 xx 3 matrix and |A| = 2, then |Adj (Adj A)|Adj(Adj A) = |
| Answer» ANSWER :A | |
| 12052. |
int_(0)^(2pi) sqrt(1-cos 2x)/(2)dx= |
|
Answer» 4 |
|
| 12053. |
Solve the following linear programming problem graphically : Maximise Z = 4x + y "…(1)" subject to the constraints : x+y le 50 "…(2)" 3x+y le 90"…(3)" x ge 0, y ge 0"...(4)" |
|
Answer» |
|
| 12054. |
A funtion f , R-{0} rarr R is defined as f(x)={{:(x^(2)+3x-7",",xgt0),(h(x)",",xlt0):}If f (x) is an odd funtion, then h(x)= |
| Answer» Answer :C | |
| 12055. |
Shortest distance between the linesbar (r )= (1 , 2, 1 ) + lambda (1,-1,1) and bar(r ) = (2,-1,-1) + mu (2,1,2)is |
|
Answer» `2/(SQRT(3))` |
|
| 12056. |
Reactify the mistakes if any. The vector vec0 has unique direction. |
| Answer» SOLUTION :INDEFINITE DIRECTION | |
| 12058. |
The solution of the differential equation ydx-(x+2y^(2))dy=0 is x=f(y). If f(f-1)=1, then f(1) is equal to : |
|
Answer» 4 |
|
| 12059. |
Let f(x)=(sin4pi[x])/(1+[x]^(2)), where [x] is the greatest integer lex, then : |
|
Answer» `f(X)` is not differentiable at some points |
|
| 12060. |
When the axes are rotated through an angle alpha, find the transformed equation of xcos alpha+ysin alpha=p. |
|
Answer» |
|
| 12061. |
The origin is shifted to (2,3) and then the axes are rotated through angle theta in the counter clock sense. If the equation 3x^(2) + 2xy + 3y^(2) - 18x -22y + 50=0 is transformed to 4x^(2) + 2y^(2) -1=0, then the angle theta = |
|
Answer» `pi/6` |
|
| 12062. |
Find the mean about the mean for the following data . (##VIK_MAT_IIA_QB_C08_SLV_003_Q01.png" width="80%"> |
|
Answer» |
|
| 12063. |
Find the particular solution of the differential equation 3e^(x) tan y dx + (1 + e^(x)) sec^(2) y dy=0, when x= 0, y= pi |
|
Answer» `(1 + e^(x))^(3) tan y=0` |
|
| 12064. |
It is given that 10% of the electric bulbs manufactured by a company are defective. In a sample of 20 bulbs, find the probability that more than 2 are defective. |
|
Answer» |
|
| 12065. |
Differentiate with respect to x: (sin x)^(x) + sin^(-1)sqrt(x) |
|
Answer» |
|
| 12066. |
consider the function f(X) =x+cosx -a values of a for which f(X) =0 has exactly one negative root are |
|
Answer» (0,1) Thus f(X) is increasing in `(-oo,oo)` as for f(x) =0 x is not forming an interval also f(X) =-cos x =0 or `x =(2n+1)(pi)/(2),nin Z` Hence there are infinite points of INFLECTION Now f(x) =1-a For POSITIVE root `1-alt0 or agt1` for negative root `1-agt 0 or a lt1` |
|
| 12067. |
{:(" "Lt),(n rarr oo):}[(1)/(na)+(1)/(na+1)+(1)/(na+2).......+(1)/(nb)]= |
|
Answer» `LOG(B/a)` |
|
| 12068. |
A and B seek admission in I.I.T. The probability that A is selected is 0.5 and the probability that both A and B are selected is atmost 0.3. The probability of B getting selected is atmost is |
|
Answer» `0.5` |
|
| 12069. |
Plot the region satisfying |x|+ |y| le 2 and |x|+|y| gt 2. |
|
Answer» Solution :`|x|+ |y| le 2` `therefore ""{{:(x+y le2",",, x ge 0"," y ge0), (x-y le 2",",, x ge 0"," y le0), (-x+y le 2",",,x le 0 ","y ge 0 ),(-x-y le 2",",,x le0 ","y le 0):}` For `x ge 0, y ge0 and x+y le 2`, we have the following region. 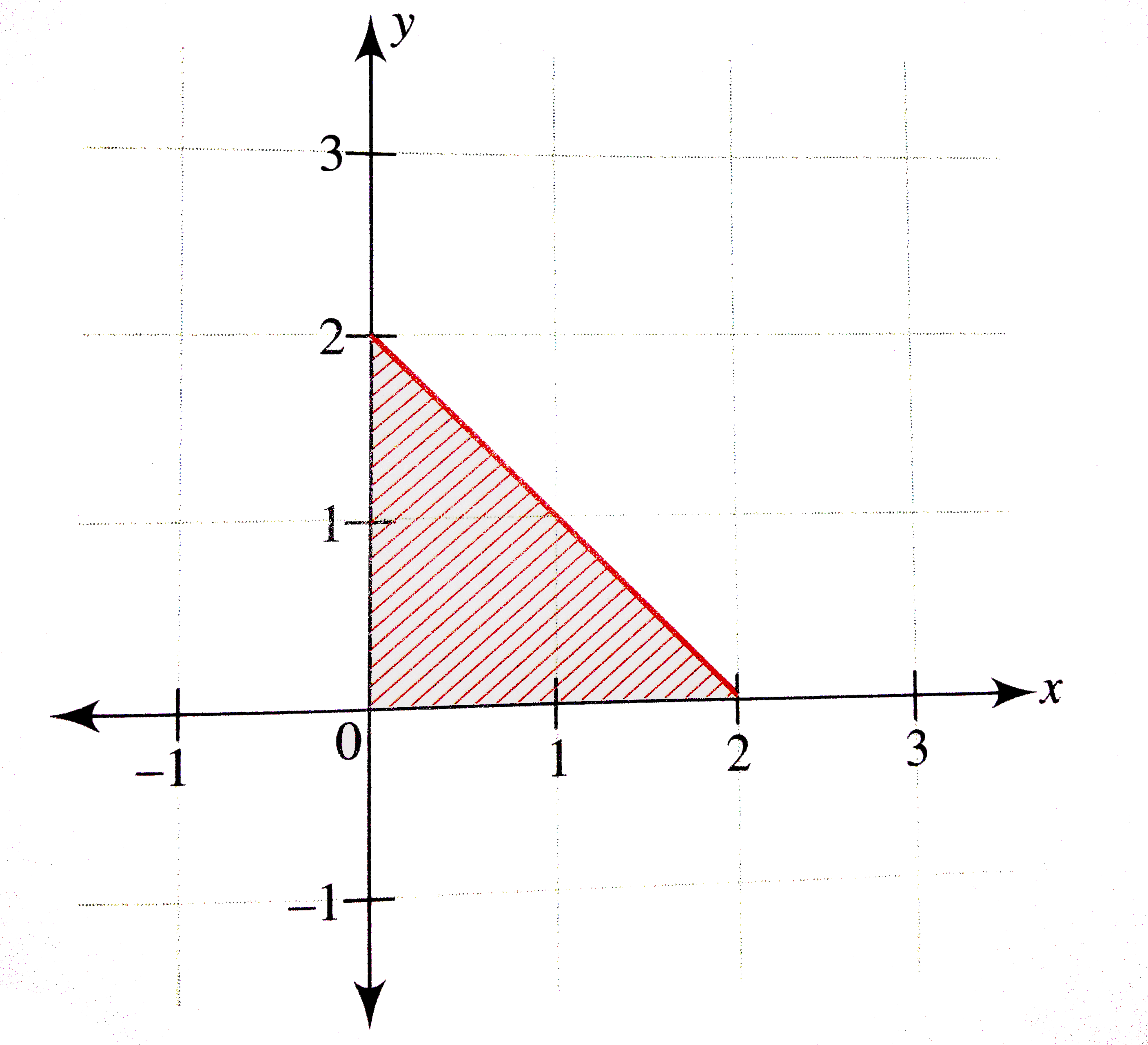 Similarly, we have other three triangles, one in each quadrant. Clubbing all four cases, we have the following region as a square.  Clearly, the POINTS satisfying `|x|+ |y| GT 2` LIE OUTSIDE the square. |
|
| 12070. |
The probability that a person chosen at random is left handed (in hand writing) is 0.1 what is the probability that in a group of ten people there is one and only one who is left handed. |
|
Answer» |
|
| 12071. |
If f(x)={((sin3x)/(e^(2x)-1),,,x!=0),(k-2,:,x=0):} is Continuous at x=0, then k= |
| Answer» | |
| 12072. |
Let f(x) (1-cos4x)/(x^(2)),g(x)=(sqrtx)/((sqrt(16+sqrtx))-4)and q(x)=(e^(2x)-x^(x)+1)/(x^(2x+e^(x)+1)),(x in R). lim_(x to 0)q(x)= |
|
Answer» 0 |
|
| 12073. |
If |bar(a)xx bar(b)|^(2)+|bar(a).bar(b)|^(2)=144 and |bar(a)|=4, then |bar(b)| is equal to ………………. |
|
Answer» |
|
| 12074. |
If x,y,z in R. xgtygtz and D= |{:((x+1)^2,(y+1)^2,(z+1)^2),(x,y,z),(1,1,1):}| , then D is ……… |
|
Answer» NEGATIVE |
|
| 12075. |
int_(0)^(pi//4) (dx)/(2+sin^(2)x)= |
|
Answer» `TAN^(-1)(SQRT(3)/2)` |
|
| 12076. |
Evaluate |[cos theta, -sin theta], [sin theta, cos theta]| |
| Answer» SOLUTION :GIVEN DETERMINANT = `cos^2 THETA + sin^2 theta = 1` | |
| 12077. |
Evaluate the definite integral in exercise overset(5) underset(4) int e^(x)dx |
|
Answer» |
|
| 12080. |
The vector equation of the line joining the pionts hat(i) - 2hat (j)+ hat k and -2 hat j + 3 hatk........ |
|
Answer» `bar r = t (hat i + hat J + hat k)` |
|
| 12081. |
For |x| lt 1, the coefficient of x^r in the expansion of ((1+x)^2)/((1-x)^3) is |
|
Answer» `2R^2 + 2r + 1` |
|
| 12082. |
Differentiate (x^2-5x+8)(x^3+7x+9)by using product rule |
| Answer» SOLUTION :REQUIRED DERIVATIVE `=(x^2-5x+8)(3x^2+7)+(x^3+7x+9)(2x-5)=3x^4+7x^2-15x^3-35x+24x^2+56+2x^4-5x^3+14x^2-35x+18x-45=5x^4-20x^3+45x^2-52x+11` | |
| 12083. |
Prove that : Expand 5sqrt(5) in increasing powers of (4)/(5). |
|
Answer» |
|
| 12084. |
Evaluate the following integrals int ((sec 2x - 1)/(sec 2x + 1)) dx |
|
Answer» |
|
| 12086. |
The product of the perpendicular distances drawn from the points (3,0) and (-3,0) to the tangent of the ellipse (x^(2))/(36)+(y^(2))/(27)=1" at "(3,(9)/(2)) is |
|
Answer» 36 |
|
| 12087. |
For the equation 2x-1=-sqrt(2-x), find the sum of the roots. |
|
Answer» `-1/4` |
|
| 12088. |
If the integral int_(b)^(oo)(sqrt(sqrtx+a)-sqrtx)-sqrt(sqrtx-sqrt(x-b)))dx is finite, then |
|
Answer» `a+2b=0` |
|
| 12089. |
If A , B are event such that P(A)=0.6, P(B)=0.4 and P(A cap B)=0.2, then find P(B | A^c) |
|
Answer» <P> SOLUTION :`P(B |A^c)=(P(BcapA^c))/(P(A^c))=(P(B-A))/(1-P(A))=(P(B)-P(ACAPB))/(1-0.6)`=`(0.4-0.2)/0.4=0.2/0.4=2/4=1/2` |
|
| 12090. |
A 1 kg block is a given a velocity of 15 m//s towards right over a very long rough plank of mass 2kg placed on a smooth horizontal surface as shown in figure. If coeficient of friction between the two blocks is equal toi 0.4 then magnitude of initial slope (in S.I unit)P_(1) versust and P_(2) versus t (in SI unit) will be: |
| Answer» Answer :C | |
| 12091. |
"CHY_SND_MAT_XII_U03_C17_E07_002_Q01.png" width="80%"> |
|
Answer» <P> |
|
| 12092. |
int_(a)^(b) x dx |
|
Answer» Solution :we know that `overset(b)UNDERSET(a)(int) f(x) dx= underset( h TO0)(" LIM") h [f(a)+f(a+h)` `+f(a+2h)+....+f{a+(n-1)h}]` ` " where " nh=b-a` ` " Here " a=a,b= b " and" f(x)=x` ` :.underset(a)overset(b)(int) x dx =underset( h to 0)("lim") h[a+(a+h)+(a+2h)` `+.....+a+(n-1)h]` `underset(h to0)("lim") h[(a+a+.....+ n " TIMES ")` `+h{1+2+.....(n-1)}]` `=underset(h to 0)("lim") [hna +h^(2).(n(-1))/(2)]` `=underset(h to 0)("lim") [hna +.(hn(nh-h))/(2)]` `=underset(h to 0)("lim")[(b-a)a+.((b-a)(b-a-h))/(2)]"(":. nh =b-a")"` `=[(b-a)a+.((b-a)^(2))/(2)]` `=(b-a)(a+(b-1)/(2))=(b-a)((2a+b-a)/(2))` `=(b-a)((a+b)/(2))=(b^(2)-a^(2))/(2)` |
|
| 12093. |
If x% of y is 10, which of the following is equal to y% of x? |
| Answer» ANSWER :C | |
| 12094. |
A 1 kg block is a given a velocity of 15 m//s towards right over a very long rough plank of mass 2kg placed on a smooth horizontal surface as shown in figure. The correct graph showing linear momentum of 1 kg (i.e P_(1)) andand 2 kg (i.eP_(2)) versus time is |
|
Answer»
|
|
| 12095. |
Statement-1:It is impossible for a system to undergo a cyclic process whose sole effects are flow ofheat into the system froma hot reservior and perform and equivalent amount of work by the system on the surroundin. Statement-2 : First law of thermodynamics is invalid for a cyclic process. |
|
Answer» Statement-1 is TRUE, statement-2 is true and statement-2 is correct explanation for statement -1 |
|
| 12096. |
If a line has direction ratios 2, -1, -2, determine its direction cosines. |
|
Answer» |
|
| 12097. |
Evaluate the definite integrals int_(0)^(pi/2)(2sinx+3)dx |
| Answer» | |
| 12098. |
An unbiased coin is tossed 5 times. Suppose that a variable X is assigned the value k when k consecutive heads are obtained for k= 3, 4, 5 otherwise X takes the value -1. The expected value of X, is ………. |
|
Answer» `(1)/(8)` |
|
| 12099. |
The vector equation of the line passing through the points (1,-2,5) and (-2,1,3) is |
|
Answer» `barr=-2hati+hatj+3hatk+lambda(3hati-3hatj+2hatk)` |
|
| 12100. |
If the angle 2 theta is acutethen the acute angle between the pair of straight lines x^(2) (cos theta - sin theta) + 2xy cos theta + y^(2) (cos theta + sin theta) = 0is |
|
Answer» `2 THETA` |
|