InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 12451. |
If (1)/((1-2x)^(2)(1-3x))=(A)/(1-2x)+(B)/((1-2x)^(2))+(C)/(1-3x) then match the following {:("List - I","List - II"),("I) A","(a) 9"),("II) B","(b) -6"),("III) C","(c) -2"):} |
| Answer» Answer :B | |
| 12452. |
int_(0)^(2a) sqrt(2ax - x^(2)) dx= |
|
Answer» `(pi a^(2))/(2)` |
|
| 12453. |
Express the 1 points geometrically in the Argrand plane. |
| Answer» SOLUTION :`1=1+i0=(1-0)` | |
| 12454. |
Show that f(x) = sinx is continuous on R . |
|
Answer» |
|
| 12455. |
By examining the chest X-ray, the probability that a person is diagonased with TB when he is actually suffering from it, is 0.99. The probability that the doctor incorrectlydiagnoses aperson to be having TB, on the basis of X-ray reports is 0.001. In a certain city , 1 in 1000 persons suffers from TB. A person is selected at random and is diagoanl to have TB. What is the chance that he actually has TB? |
|
Answer» Solution :LET E= event that the DOCTOR diagonoses TB, `E_1` =event that the person selected is SUFFERING from TB, and `E_2` =event that the person selected is not suffering from TB. Then , `P(E_1)=1/1000andP(E_2)=(1-1/1000)=999/1000`. `P(E//E-1)`= probability that TB is diagnosed, when the person actually has TB `=99/100` `P(E//E-2)`= probability that TB is diagnosed, when the person has no TB `=1/1000` Using Bayes's theorem, we have `P(E_1//E)`= probability of a person actually having TB, if it is knows that he is diagonal to have TB `(P(E//E_1) .P(E_1))/(P(E//E_1).P(E_1)+P(E//E_2).P(E_2))` `=((99/100xx1/1000))/((99/100xx1/1000)+(1/1000xx999/1000))=110/221`. Hence, the REQUIRED probability is `110/221`. |
|
| 12456. |
Integrate the functions xcos^(-1)x |
|
Answer» |
|
| 12457. |
Which of the following options is the only CORRECT combination ? |
|
Answer» <P>(I) (III) ( R) |
|
| 12458. |
Which of the following options is the only CORRECT combination ? |
|
Answer» (III) (II) (S) |
|
| 12459. |
Using method of integration, find the area (in sq. units) of the smaller portion enclosed between the curves, x^2 + y^2 = 4 and y^2 = 3x. |
|
Answer» |
|
| 12460. |
The remainder of n^(4)-2n^(3)-n^(2)+2n-26 when divided by 24 is |
|
Answer» 20 |
|
| 12461. |
If f(x)={(|4x-5[x], , , "for" xgt1),([cos pix],,, "for" x le1):} where [.] is greatest integer function, then mis the number of points of discontinuity off(x) and n is the number of points of non-differentiability in [0,2]then evaluate(m+n). |
|
Answer» |
|
| 12462. |
Prove that x^3+y^3+z^3-3xyz =(x+y+z)(x+omegay+omega^2z)(x+yomega^2+z omega) |
|
Answer» SOLUTION :`R.H.S.=(x+y+z)(x+omegay+omega^2z)(x+yomega^2+zomega)` `=(x+y+z)(x+xyomega^2+zxomega+xyomega+y^2omega^3+yzomega^2+zxomega^2+yzomega^4+z^2omega^3)` `=(x+y+z)[x^2+y^2+z^2+XY(w^2+w)+xy(omega^2+omega)+ZX(omega^2+omega)]` `(x+y+z)[x^2+y^2+z^2-xy-yz-zx)` `=x^3+y^3+z^3-3xyz="L.H.S.(PROVED)"` |
|
| 12463. |
Which of the following species have partially filled d-subshell ? |
| Answer» | |
| 12464. |
An urn contains 5 red and 5 black balls. A ball is drawn at random, its colour is noted and is returned to the urn. Moreover, 2 additional balls of the colour drawn are put in the urn and then a balls is drawn at random.What is the probability that the second ball is red ? |
|
Answer» |
|
| 12465. |
The equation to the locus of the midpoints of chords of the circle x^(2)+y^(2)=r^(2) having a constant length 2l is |
|
Answer» `X^(2)+y^(2)-L^(2)-r^(2)` |
|
| 12466. |
int(sqrtx)/(sqrt(x)+root(3)x)dx= |
|
Answer» `x-(6)/(5)ROOT6(x^5)+(3)/(2)root3(x^2)-2sqrtx+3root3x-6root6x+6log|root6x+1|+c` |
|
| 12467. |
There are 10 seats in the 1st row of a movie theatre. 4 persons enter and take seats randomly in this row. Find the probability that out of any two seats located symmetrically about the middle of the row, atleast one is empty. |
|
Answer» |
|
| 12468. |
The points A,B,C are randomly selected on the circumference of a circle. Find the probability that the points lie on a semi circle. |
|
Answer» |
|
| 12469. |
Let pi be the plane passing through the points hat(i), hat(j), hat(i)+hat(j)+hat(k) and L be the line passing through the point hat(i)+2hat(j)+3hat(k) and parallel to the vector hat(i)-hat(j)+hat(k). If P(alpha, beta, gamma) is the point of intersection of the plane pi and line L, then sqrt((alpha^(2)+beta^(2))gamma^(2))= |
| Answer» ANSWER :C | |
| 12470. |
If the tangents drawn from a point on the hyperola x^(2)-y^(2)=a^(2)-b^(2) to the ellipse x^(2)/a^(2)-y^(2)/b^(2)=1 makes angles alpha and beta with transverse axis of the hyperbola, then |
|
Answer» `TAN ALPHA-tan beta=1` |
|
| 12471. |
The plane barr = s(i+2j-4k) +t(3i+4j-4k) +(1-t)(2i-7j+3k) is parallel to the line |
|
Answer» `BARR=(-i+j-k)+t(-i-2j+4k)` |
|
| 12472. |
Prove that the functions (a) f(x)=x+sin x, (b) f(x)=cos sqrt(x) are non-periodic. |
|
Answer» |
|
| 12473. |
Which of the following graphs represents the soution set for 5x - 10y gt 6 ? |
|
Answer»
|
|
| 12474. |
IFtanA and tanBare therootsofabx^2- c^2 +ab =0 wherea,b,care thesidesof thetriangleABCthen thevalueofsin ^2+ sin^2B+ sin ^2 C is |
|
Answer» 1 |
|
| 12475. |
The smaller area between the ellipse (x^(2))/(9)+(y^(2))/(16)=1 at the line (x)/(3)+(y)/(4)=1 is |
|
Answer» `pi-2` |
|
| 12476. |
If the point on y = x tan alpha- (ax^(2))/(24^(2) cos^(2) alpha) (alpha gt0) where the tangent is parallel to y=x has an ordinate u^(2)//4a, then cos^(2) alpha is equal to |
|
Answer» |
|
| 12478. |
Let alpha be a root of the equation x^2-x+1=0, and the matrix A=[(1,1,1),(1,alpha,alpha^2),(1,alpha^2,alpha^4)] and matrix B=[(1,-1,-1),(1,alpha,-alpha^2),(-1,-alpha^2,-alpha^4)] then the value of |AB| is : |
|
Answer» 1 `ALPHA=-omega` `AB=[(1,1,1),(1,alpha,alpha^2),(1,alpha^2,alpha^4)] [ (1,-1,-1),(1,alpha,-alpha^2),(-1,-alpha^2,-alpha^4)]` `AB=[(1+1-1,-1+alpha-alpha^2,-1-alpha^2-alpha^4),(1+alpha-alpha^2,-1+alpha^2-alpha^4,-1-alpha^3-alpha^6),(1+alpha^2-alpha^4, -1+alpha^3-alpha^6,-1-alpha^4-alpha^8)]` SUBSTITUTING `alpha=-omega` and simplifying , we get `AB=[(1,0,0),(2,2omega^2,-1),(-2omega, -3,0)]` , |AB|=3 |
|
| 12479. |
If x=alpha, y=beta, z=gamma is the solution of the system of equations x+y+z=4, 2x-y+3z=9, 3x+y+2z=8, "then "4alpha+2beta+3gamma= |
|
Answer» 0 |
|
| 12480. |
The number of ways in which 10 candidates A_(1),A_(2),A_(3),.........,A_(10) can be ranked so that A_(1) is always above A_(10) is |
| Answer» ANSWER :D | |
| 12482. |
If alpha+ beta + gamma = 6, alpha^(2) + beta^(2) + gamma^(2) = 14and alpha^(3) + beta^(3) + gamma^(3) = 36,then alpha^(4) + beta^(4) + gamma^(4) = |
|
Answer» 98 |
|
| 12483. |
Assertion(A ) : the rootsx^4 -5x^2+6=0are+- sqrt(2) ,+-sqrt(3) Reason (R ) : theequation having the rootsalpha_1 , alpha_2 , ….., alpha_n is(x-alpha_1) ( x- alpha_2 )…. (x-alpha_n)=0 |
|
Answer» BOTHA and RaretrueR ISTHE correctexplanationof A |
|
| 12484. |
If x=cisalpha,y=cisbeta" then " x^3y^4-(1)/(x^3y^4)= |
|
Answer» `2icos(3alpha+4beta)` |
|
| 12485. |
The regression equation of x on y is 9x-2y-38=0. If mean of x series is 6, then mean of y series is |
|
Answer» a) 8 |
|
| 12486. |
A river flows due North, and a tower stands on its left bank. From a point A upstream and on the same bank as the tower, the elevation of the tower is 60^(@), and from a point B just opposite A on the other bank the elevation is 45^(@). If the tower is 360 m high, the breadth of the river is |
|
Answer» `120 sqrt(6)` m |
|
| 12488. |
Integrate the functions (x^(3)sin(tan^(-1)x^(4)))/(1+x^(8)) |
|
Answer» |
|
| 12489. |
Find the common tangent of y=1+x^(2) and x^(2)+y-1=0. Also find their point of contact. |
|
Answer» `(0, -4)` |
|
| 12490. |
If (sin(xy))/(1+cos(xy)) |
|
Answer» `(X^(2)-y^(2))/(x-y)` |
|
| 12491. |
Three bags contain a number of red and white balls as follows: The probability that bag i will be chosen and a ball is selected from it is (i)/(6), i = 1, 2, 3. What is the probability that, (i) a red ball will be selected ? (ii) a white ball is selected ? |
|
Answer» |
|
| 12492. |
Two particles A,B are moving on two concentric circles of radii R_1) and R_2 with equal angular speed omega. Att=0,their positions and direction fo motion are shown in the figure : |
|
Answer» `OMEGA(R_1+R_2)HATI` |
|
| 12493. |
Find the area of the region {(x,y): x^2 +y^2 le 2ax , y^2 le ax , x le 0 , y le 0 } |
|
Answer» Solution :Clearly we have to find the area of the region lying in the first quadrant `(x ge 0, y ge 0 )` included between the CIRCLE `x^(2)+y^(2)=2ax` and the PARABOLA `y^2 =ax` Thus , the equations of the given curves are `x^2+y^2 =2ax…(i)` and`y^2 =ax` ...(II) Now , clearly `x^2+y^2=2ax ` is a circle with its CENTER `B(a,0)` and radius `=a` units And `y^2=ax ` is parabola with `O(0,0)` as its vertexand the x-axis as its axis. We can draw its figure as shown . Their points of intersection may be obtained by solving `(i)` and `(ii)` and keeping in view that `x ge 0 and y gt 0` Using `(ii)` in `(i)` ,we get `x^2-ax =0 rArr x(x -a) =0` `rArr x=0 or x =a` Now `(x=0 rArr y=0 )` and `(x=a rArr y=a)` Thus, two curves intesect at O(0,0) and A(a,a) `therefore" required area " =UNDERSET(0)overset(a)int sqrt(2ax -x^2)dx - underset(0)overset(a)int sqrt(ax)dx` `=underset(0)overset(a)intsqrt(a^2-(x-a)^2)dx -sqrt(a).underset(0)overset(a)int sqrt(x)dx ` `=[((x-a)sqrt(a^2-(x-a)^2))/(2)+a^2/2 sin^(-1)""((x-a)/a)]_0^a-sqrt(a)[2/3x^(3//2)]_0^a` `={a^2/2sin^(-1)(0)-a^2/2 sin^(-1)(-1)-2/3a^2}` `=((pia^2)/4-2/3a^2)`sq units Hence, the required area is `=((pia^2)/4-2/3a^2)` sq units . 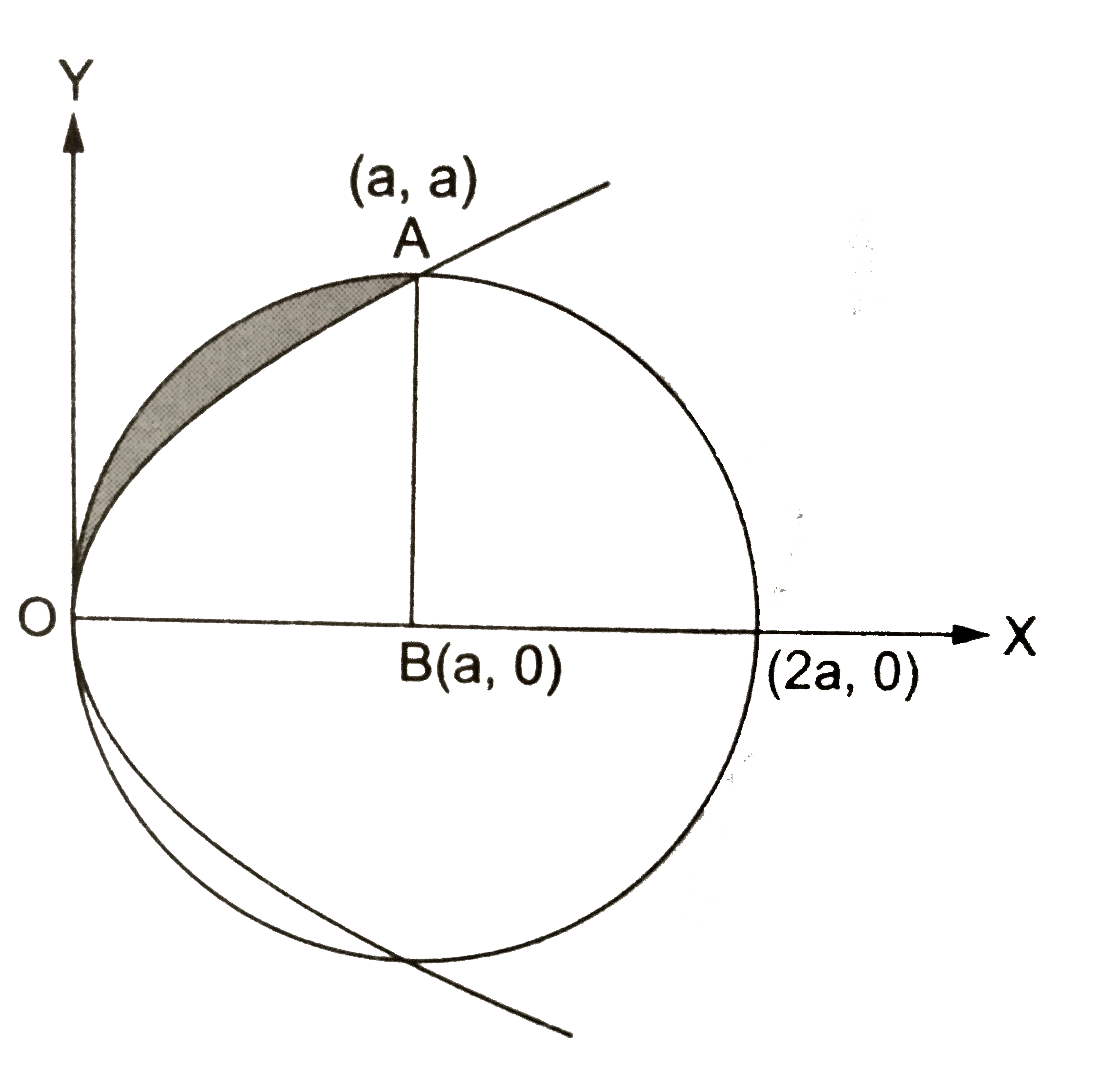
|
|
| 12494. |
If alpha,beta,gamma are the rootsof x^3-2x^2+3x-4=0 find the value of sumalpha^2 |
|
Answer» |
|
| 12495. |
Integrate the following functions: 1/(sinx cos^3x) |
|
Answer» Solution :`1/(sinx cos^3x) = COSX/(sinx cos^4x) = sec^4x/tanx` =`(sec^2x(1+tan^2x))/tanx` Put tan X =t. Then dt = `sec^2x dx` , therefore` int dx/(sinx cos^3x) = int(1+t^2)/t dt` =`int(1/t+t)dt = log|t|+t^2/2+c` `log|tanx|+tan^2x/2+c` |
|
| 12496. |
An ionic solid PQ crystallises in rocksaltstructure with density 4.0gm//cm^(3).If theradius of cation and anion is 83 and 167 pm respectively, then the molar mass of solid is[N_(A)=6xx10^(23)] |
|
Answer» 75 gm/`CM^(3)` `DELTA=(ZxxM)/(N_(A)xxa^(3)xx10^(-30))=(4xxM)/(6.02xx10^(23)xx[500]^(3)xx10^(-30))=4` M=75.25 gm / mole |
|
| 12497. |
If cos (alpha + beta) = 4/5, sin (alpha -beta) = 5/13 and alpha, betabetween 0 and pi/4, thentan 2 alphais equal to |
|
Answer» `56/33` |
|
| 12498. |
If I_(n)=int_(0)^(pi//4) tan^(n)theta d thetafor 1,2,3,… then I_(n-1)+I_(n+1)= |
| Answer» ANSWER :3 | |
| 12499. |
Resolve (x^(2)+1)/(x^(4)+x^(2)+1) into partial fractions. |
|
Answer» |
|
| 12500. |
Find the area of the region in the first quadrant enclosed by x-axis, line x = sqrt3y and the circle x^(2) + y^(2) = 4. |
|
Answer» |
|