InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 27151. |
Integrate the following functions. int(x^(2)+1)/(x^(4)+1)dx |
|
Answer» |
|
| 27152. |
Which of the following , taken by itself, would be decreasing the rate at which energy is transferred by a way travelling along a straight ? |
|
Answer» reducing the linear MASS density of the string by one half `((dE)/(dt))_(AV)=(1)/(2)muvomega^(2)A^(2)=(1)/(2)mu((f)/(LAMBDA))omega^(2)A^(2)=(1)/(4pi)mu(omega^(2))/(lambda)A^(2)` `((dE)/(dt))_(av)=(1)/(2)SQRT(Tmu)omega^(2)A^(2)` `v=sqrt((T)/(mu))` |
|
| 27153. |
The ratio in which the point Q(5,4,-6) divides the line joining the points P(3,2,-4) and R(9,8,-10) is |
|
Answer» `2:1` |
|
| 27154. |
Let A and B be independent events with P(A) = 0.3 and P(B) = 0.4. Find (i) P(A cap B) (ii) P(A cup B) (iii) P(A|B) (iv) P(B|A) |
|
Answer» |
|
| 27155. |
If each element of a second order determinant is either zero or one, what is the probability that the value of the determinant is positive? (Assume that the individual entries of the determinant are chosen independently, each value being assumed with probability (1)/(2)) |
|
Answer» |
|
| 27156. |
If x e ^(xy) = y + sin ^(2) x, thenat x =0, (dy)/(dx) = |
|
Answer» 1 |
|
| 27158. |
An equailateral triangle is inscribed in the parabola y^(2)=4ax whose vertex is at the vertex of the parabola . The length of its side is |
|
Answer» `2sqrt(3)`a |
|
| 27159. |
A cylindrical tank of radius 10m is being filled with wheat at the rate of 314 cubic metre per hour. The depth of the wheat is increasing at the rate of |
|
Answer» 1 m/h |
|
| 27160. |
For events A and B if P(A) = 0.7, P(B) = 0.5 and P(A cap B)= 0.3 then find P(A |B). |
|
Answer» |
|
| 27161. |
Let H be a hyperbola of eccentricity 3. A normal to the hyperbola meets the transverse axis and the conjugate axis at P and Q, respectively. If locus of midpoint of PQ is a hyperbola of eccentricity elt then er is equal to |
|
Answer» |
|
| 27162. |
(Manufacturing Problem) A manufacturer considers that men and women workers are equally efficient and so he pays tehm at the same rate.He has 30 and 17 units of workers(male and femlae) and capital respectively, which he uses to produce two types of goods A and B.To produe one unit of A, 2 workers and 3 units of capital are required whie 3 workers and 1 unit of capital are required to produce one unit of B. If A and B are priced at ₹. 100 and₹.120 per unit respectively, how should he use his resources to maximise the total revenue?Form the above as an LPP and solve graphically. |
|
Answer» |
|
| 27163. |
If P(A) = 0.4, P(B)=0.5, P(C) =0.6, P(AcapB) = 0.2, P(BcapC) = 0.3, P(CcapA) = 0.25, P(AcapBcapC) = 0.1 then P(AcupBcupC) = |
|
Answer» |
|
| 27164. |
Let f be a continuous function satisfying f (x+y) = f (x) + f (y), for each x, y in R and f(1) = 2 then int(f(x)tan^(-1)x)/((1+x^(2))^(2))dx is equal to |
|
Answer» cannot be DETERMINED explicity |
|
| 27165. |
Find the shortest distance between the ellipse x^(2) + 2y^(2) = 2 and the circle x^(2)+y^(2)-3x-2sqrt(2)y+4=0 |
|
Answer» |
|
| 27166. |
How many geometrical isomers are possible for the given complex ? Pt(gly)Cl_(2)BrI]^(-) [If your answer is 2 then write the answer as 0002.] |
Answer» Solution :`]PT(gly)Cl_(2)BrI]^(-)toM(AB)c_(2)de` 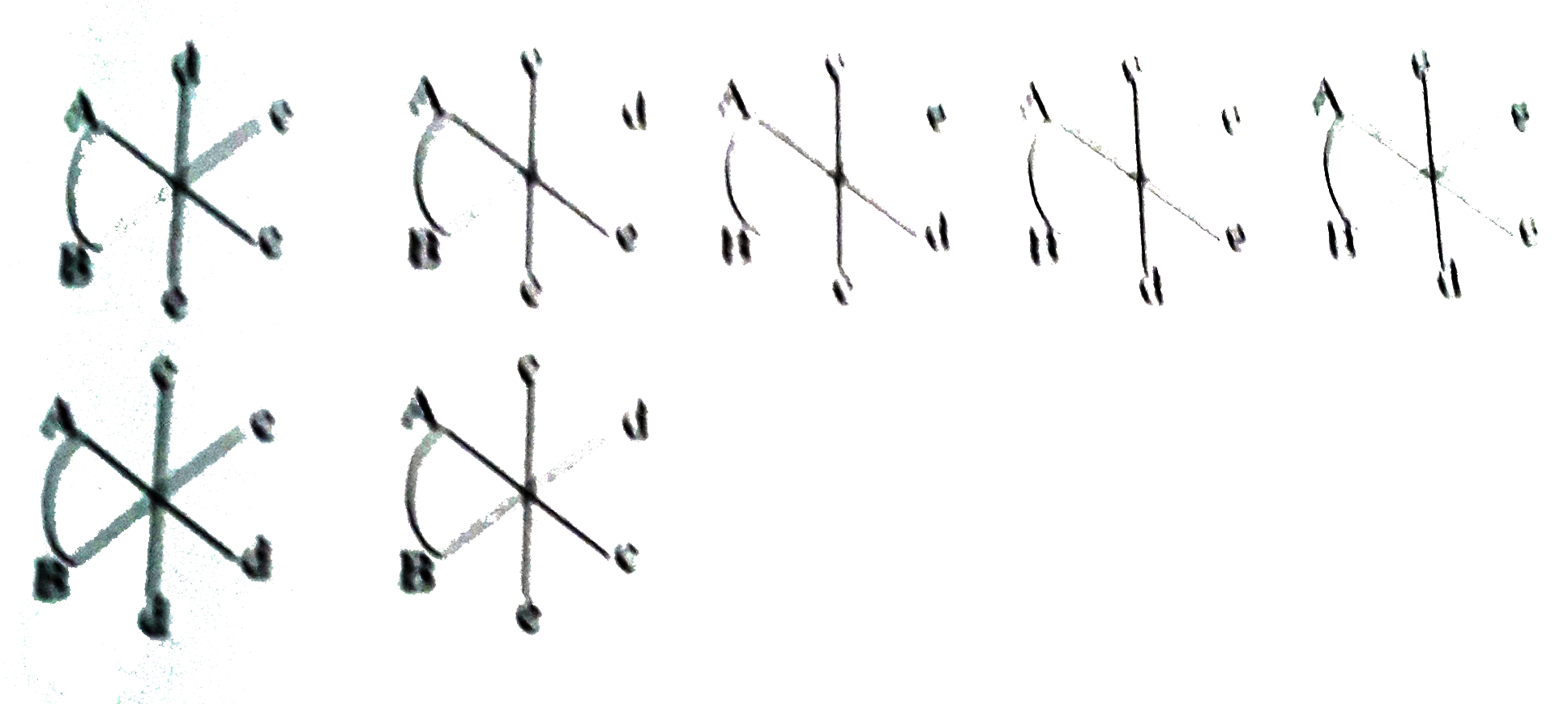
|
|
| 27167. |
Find area of the triangle with vertices at the point given in each of the following: ( -2,-3) , (3,2) ,( -1,-8) |
|
Answer» |
|
| 27168. |
sec^(2) (tan^(-1) 4) + cosec^(2) (cot ^(-1) 3) =? |
|
Answer» 30 |
|
| 27169. |
Two unit squares are chosen at random on a chess board. Find the probability that they have a side in common. |
|
Answer» |
|
| 27170. |
A solution is to be kept between 68^@ F and 77^@ F. what is the range in temperature in degree Celsius (C) if the Celsius/ Fahrenheit (F) conversion formula is given by F = 9/5 C + 32? |
|
Answer» |
|
| 27171. |
If I_(n) = int_(0)^(1) (1- x^(5) )^(n) dx, then (I_(21) )/( I_(20) ) is equal to |
|
Answer» |
|
| 27172. |
If two circles touching both the axes intersect at two points P and Q where P=(3,1) then PQ= |
|
Answer» `SQRT(2)` |
|
| 27173. |
Sand is pouring from a pipe at the rate of 12 cm^(3)//s. The falling sand forms a cone on the ground in such a way that the height of the cone is always one-sixth of the radius of the base. How fast is the height of the sand cone increasing when the height is 4cm? |
|
Answer» |
|
| 27174. |
If veca and vecb are parallel vector, then [(veca,vecb,vecc)] is equal to |
|
Answer» 2 |
|
| 27175. |
For the function f(x)= x + (1)/(x), x in [1, 3] the value of c for mean value theorem is |
| Answer» Answer :B | |
| 27176. |
if (4,k) and (2,3) are conjugate points with respect to the circle x^(2) + y^(2) = 17 then find k. |
|
Answer» |
|
| 27177. |
If f:RrarrR_(1)f(x) is a differentiable bijective function, then which of the following may be true. |
|
Answer» `(f(x)-x)f''(x)LT0,AAx in R` |
|
| 27178. |
Find the absolute maximum value and the absolute minimum value of thefunctions in the given intervals: f(x) = (x-1)^(2) +3, x in[-3 ,1) |
|
Answer» |
|
| 27179. |
From a point P(x_(1),y_(1)) on the straight line 4x-3y+14=0 two tangents PA and PB are drawn to the circles x^(2)+y^(2)=16 and x^(2)+y^(2)+8x-6y+12=0, then |
|
Answer» PA=PB |
|
| 27180. |
Find the absolute maximum value and the absolute minimum value of thefunctions in the given intervals: f(x) = 4x -(1)/(2) x^(2) , x in [-2,(9)/(2)] |
|
Answer» |
|
| 27181. |
The two adjacent sides of a parallelogram are 2hati-4hatj+5kandhati-2hatj-3hatk. Find the unit vector parallel to its diagonal Also , find its area. |
|
Answer» |
|
| 27182. |
If two dice are thrown and at least one of the dice shows 5.then the probability that the sum is 10 or more is |
|
Answer» `(1)/(6)` N (A) = 11 . and n(s) ` = 6 XX 6 = 36` B = Eventof Showingshows10 or morewhenat lest onedice SHOWN 5. ` = (5,5) ,(5,6),(6,5)` n(B) = 3 . `rArr n(A nn B) = 3` Now, `P((B)/(A)) = (P(AnnB))/(P(A))` . `=((n(AnnB))/(n(S)))/((n(A))/(n(S))) = ((3)/(36))/((11)/(36)) = (3)/(11)` |
|
| 27183. |
Assertion(A ) :thenumberof rootsof x^4+2x^3 -7x^2 -8x +12=0Reason (R ) :Everyalgebraicequationofdegree n hasn rootsandnomore. |
|
Answer» BOTHA and RaretrueR ISTHE correctexplanationof A |
|
| 27184. |
Let I_(n)=int_(0)^(pi//2) cos^(n)x cos nx dx. Then, I_(n):I_(n+1) is equal to |
|
Answer» `3:1` |
|
| 27185. |
Let f(x)=[x]= Greatest integer less than or equal to x and k be an integer. Then, which one of the following in not correct? |
|
Answer» `lim_(xtok^-)f(x)=K-1` `THEREFORE ("LHS at" x =k)` `=lim_(xtok^-)f(x)=lim_(hto0)=lim_(hto0)f(k-h)=lim_(hto0)[h-k]` `=lim_(hto0)k-1=k-1[because k-1ltk-hltk-hlt ktherefore [k-h]=k-1]` `therefore (RHL "at" x=k)` `=lim_(xto0)f(x)=lim_(hto0)f(k-h)=lim_(hto0)[k+h]` `=lim_(hto0)k=k[because klt k+hlt k+1therefore [k+h]=k]` Clearly, `lim_(xt0k^+)f(x) ne lim_(xtok^+)f(x). So, lim_(xtok)f(x)` does not exist. |
|
| 27186. |
H(x) increase as f(x) decreases for all real values ofx if |
|
Answer» `a in (0,3)` `3a(f(x))^(2)-2 AF(x)+le for all x in R` or `33a LT 0and 4a^(2)-12ale 0` or `a lt 0 and a in [0,3]` So , such AIS possible |
|
| 27188. |
When three cards are drawn at random from a well shuffled pack of cards, then what is the probability that all of them are from the different suits? |
|
Answer» `(""^(13)C_(3))/(""^(52)C_(3))` |
|
| 27189. |
Derivative of tan^(-1)x w.r. to cot^(-1)x is ……. Where x in R |
|
Answer» `-1` |
|
| 27190. |
Let f(x) = int_(0)^(x)(dt)/(sqrt(1+t^(2))) and g(x)be the inverse of f(x), then which one of the followingholds good ? |
|
Answer» `2G" = G^(2)` |
|
| 27191. |
(i) Find the length of the chord intercepted by the circle x^(2)+y^(2)-8x-2y-8=0 on the line x+y+1=0 (ii) Find the length of the chord intercepted by the circle x^(2)+y^(2)+8x-4y-16=0 on the line 3x-y+4=0 (iii) Find the length of the chord formed by x^(2)+y^(2)=a^(2) on the line xcos alpha +y sin alpha=p |
|
Answer» |
|
| 27192. |
int_(0)^(1)[2x]dx where [] is the greatest integer function : |
|
Answer» 1 |
|
| 27193. |
IFalpha,betaare therootsofax^2 + bx+ c=0and s_(n)= alpha ^n + beta ^nthen|(3,1+S_1,1+S_2),(1+S_1,1+S_2,1+S_3),(1+s_(2),1+s_3,1+S_4)|= |
|
Answer» 0 |
|
| 27194. |
Let the terms a_(1),a_(2),a_(3),…a_(n) be in G.P. with common ratio r. Let S_(k) denote the sum of first k terms of this G.P.. Prove that S_(m-1)xxS_(m)=(r+1)/rSigmaSigma_(i le itj le n)a_(i)a_(j) |
|
Answer» Solution :We have `a_(1)+a_(2)+…+a_(m))^(2)` `=a_(1)^(2)+a_(2)^(2)+…+a_(m)^(2)+2(a_(1)a_(2)+a_(2)a_(3)+…)` `THEREFORE[(a_(1)(1-r^(m)))/(1-r)]^(2)=(a_(1)^(2)(1-r^(2m)))/(1-r^(2))+2underset(1leiltjlen)(SigmaSigma)a_(i)a_(j)` `rArr2underset(1leiltjlen)(SigmaSigma)a_(i)a_(j)=(a_(1)^(2)(1-r^(m))^(2))/((1-r)^(2))-(a_(1)^(2)(1-r^(2m)))/(1-r^(2))` `=(a_(1)^(2)(1-r^(m)))/((1-r)^(2)(1+r))2(r-r^(m))` `=(2R)/(1+r){a_(1)cdot((1-r^(m-1)))/(1-r)}{(a_(1)(1-r^(m)))/(1-r)}` `=S_(m-1)xxS_(m)` |
|
| 27196. |
A: If (5+ sqrt(24))^n=I+F where, I, n are positive integers, 0 lt F lt 1 then I is an odd integer and (I+F)(1-F)=1. R : If (a+sqrtb)^=I+F where I, n are positive integers, 0 lt F lt1, a^2 - b=1 then i) I is an odd positive integer ii) (I+F)(1-F)=1. |
|
Answer» Both A and R are true and R is the CORRECT EXPLANATION of A |
|
| 27197. |
The simplest formular of a compound containing 50% of element X (atomic mass 10) and 50% pf element Y (atomic mass 20) is :- |
|
Answer» XY |
|
| 27198. |
Write the Macleaurin series expansion of the following functions: (i)e^(x)(ii) sin x (iii) cos x (iv) log (1-x):-1 lt x lt 1(v) tan ^(-1)(x),-1 lt x lt 1(iv) cos ^(2)x |
|
Answer» |
|
| 27199. |
IFA+B+C =pi , thentan ((A)/(2))tan ((B)/(2)) + tan (B/2)tan(C/2) + tan(C/2 )tan ((A)/(2))is |
| Answer» ANSWER :D | |
| 27200. |
Solve the inequality P(x)=x^(3)-4x^(2)+x+4 gt0. |
Answer» Solution :USE a calculator to GRAPH `y=P(x)` and find its (approximate) ZEROS: `-0.814,1.471, and 3.343`.  Observe that the graph of `y=P(x)` is above the x-axis for -0.814`ltxlt1.471` or `x GT 3.343`. |
|