InterviewSolution
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 3501. |
Find the coordinates of the foot of the perpendicular drawn from the point (-1,2,3) to the straight line vec(r)=(veci-4hatj+3hatk)+t(2hati+3hatj+hatk) . Also , find the shortest distance from the given point to the straight line. |
|
Answer» |
|
| 3502. |
Corner points of the feasible region for an LPP are (0, 2), (3, 0), (6, 0), (6, 8) and (0, 5). Let F = 4x + 6y be the objective function. (Maximum of F)-(Minimum of F) = |
|
Answer» 60 |
|
| 3503. |
If x^(3) + x^(2)y + xy^(2) + y^(3) = 81 find (dy)/(dx). |
|
Answer» |
|
| 3504. |
Find (dy)/(dx)," if "y=sec^(-1) ((1)/(2x^(2)-1)), 0 lt x lt (1)/(sqrt2) |
|
Answer» |
|
| 3505. |
If the circle x^(2)+y^(2)=r^(2) intersects the hyperbola xy=c^(2) in four points (x_(i),y_(i)) for i=1,2,3 and 4 then y_(1)+y_(2)+y_(3)+y_(4)= |
|
Answer» 0 |
|
| 3506. |
Find the maximum bumber of electron inCr havin m=0? |
|
Answer» |
|
| 3507. |
A and B are two square matrices such that A^(2)B=BA and if (AB)^(10)=A^(k)B^(10) then the value of k-1020 is. |
|
Answer» |
|
| 3508. |
If the angle between the lines whose direction cosines are -(2)/(sqrt(21)),( C)/(sqrt(21)),(1)/(sqrt(21)) and (3)/(sqrt(54)),(3)/(sqrt(54)),(6)/(sqrt(54)) is (pi)/(2), then the value of C is |
|
Answer» 6 |
|
| 3509. |
If area bounded by the curve x^(2)y+y^(2)x=alpha y is 2 units, then possible values of alpha is/are |
| Answer» Answer :A | |
| 3510. |
Find all the values of (8i)^(1//3) and hence find sum and product of their values. |
|
Answer» Product of the values `=(sqrt3+i)(-sqrt3+i)(-2i)=8i` |
|
| 3511. |
If A+B+C=270^(@) then sin 2A+sin2B+sin2C= |
|
Answer» `4sinA SIN B sin C` |
|
| 3512. |
Contra-positive of p rarr ( q rarr r ) is logically equivalent to |
|
Answer» `p RARR ( q rarr R ) ` |
|
| 3513. |
f is a differentiable function defined on an interval I with positive derivative . Then f is ........... |
|
Answer» INCREASING on I |
|
| 3514. |
log5-(log25)/(2^(2))+(log125)/(3^(2))-(log625)/(4^(2))+ …… |
|
Answer» LOG 2 |
|
| 3515. |
A plane whose normal has direction ratios lt 3, -2, k gt is parallel to the line joining (-1,1,- 4) and (5,6,-2). Then the value of k =........[6,-4,-1,0] |
|
Answer» 6 |
|
| 3516. |
Choose the incorrect statementfrom thefollowing : |
|
Answer» `tan^(-1) (tanx) = X` if and only if `(-PI)/2 LT x lt (pi)/2` |
|
| 3517. |
Construct a 3xx4 matrix A=[a_(ij)] whose elements are given by a_(ij)={{:(3i-2j",""where "i nej,),(0",""where"i=j,):} |
|
Answer» |
|
| 3518. |
In the expansionof (y^3+a^7/y^5)^10,Does there exist a term independent of y in the above expansion? |
|
Answer» SOLUTION :LET (r+1)th term is independent of y. THEREFORE `y^(30-8r)` = 1 = `y^0` or, 30-8r = 0 or, r = 30/8 = 15/4 which is not possible as `RIN N` or zero. therefore There is no term in the expansion of `(y^3+a^7/y^5)^10` which is independent of y. |
|
| 3519. |
Let f(x)=sin ^(4)x] then( where[.]represents thegreatest integer function ). |
|
Answer» F(X)is continuous at x=0 |
|
| 3520. |
Statement -1: f(x) = x^(3)-3x+1 =0 has one root in the interval [-2,2]. Statement-2: f(-2) and f(2) are of opposite sign. |
|
Answer» Statement-1 : is TRUE, Statement-2 is True, Statement-2 is a CORRECT explanation for Statement-1 |
|
| 3521. |
Evaluate the following determinants.[[0.2,0.1,3],[0.4,0.2,7],[0.6,0.3,2]] |
|
Answer» SOLUTION :`[[0.2,0.1,3],[0.4,0.2,7],[0.6,0.3,2]]` `2[[0.1,0.1,3],[0.2,0.2,7],[0.3,0.3,2]]=0(because C_1=C_2)` |
|
| 3522. |
IF(x^2 )/(a^2)+(y^2)/(b^2)=1, then(d^2y)/(dx^2)= |
|
Answer» `-(b^4)/(a^2y^3)` |
|
| 3523. |
Find (dy)/(dx) when x and y are connected by the relation given: tan^(-1) (x^(2) + y^(2))=a |
|
Answer» |
|
| 3524. |
The value of determinant |{:(a-b,b+c,a),(b-a,c+a,b),(c-a,a+b,c):}| |
|
Answer» `a^3+b^3+c^3` |
|
| 3525. |
Using differentials, find the approximate values of the following: 1/(2.002)^(2) |
|
Answer» |
|
| 3526. |
If each of the observation x_(1), x_(2), ...,x_(n) is increased by 'a', where a is a negative or positive number, show that the variance remains unchanged. |
|
Answer» |
|
| 3527. |
What is the total number of different diagonals of a given pentagon? |
|
Answer» Solution :The TOTAL number of DIFFERENT diagonals of given pentagon is `(""^5P_2)/(2!)-5=10-5=5.` |
|
| 3528. |
A variable point P is chosen on the straight line x + y = 4 and tangents PA and PB are drawn from it to circle x^(2) + y^(2) = 1 . Then the position of P for the smallest length of chord of contact AB is |
|
Answer» (3,1) |
|
| 3529. |
Find the equation of louse of a point which is equidistant from the coordinate axes. |
|
Answer» |
|
| 3530. |
Let O be a point inside DeltaABC such that angleOAB = angleOBC = angle OCA = theta cosec^(2) A + cosec^(2)B + cosec^(2)C is equal to |
|
Answer» `cot^(2) theta`  Applying sine rule in `DeltaAOB`, we have `(OA)/(sin angleABO) = (AB)/(sin angle AOB)` or `OA = (c sin angleABO)/(sin angleAOB) = (c sin (B - theta))/(sin B)`...(i) `[ :' angle ABO = B - theta, angle AOB = 180^(@) - theta - angleABO = 180^(@) -B]` Again in `DeltaAOC`, we have `(OA)/(sin angleACO) = (AC)/(sin angleAOC)` `RARR OA = (b sin angleACO)/(sin angleAOC) = (b sin theta)/(sin A)` `[ :' ANGLEOAC = A - theta, angleAOC = 180^(@) - theta - angleOAC = 180^(@)]` From Eqs. (i) and (ii), we have `(c sin (B - theta))/(sin B) = (b sin theta)/(sin A)` or `c sin A (B - theta) = b sin theta sin B` `= b sin theta sin (A +C)` or `2R sin C sin A (sin B cos theta - cos B sin theta)` `= 2R sin B sin theta (sin A cos C + cos A sin C)` Dividing both sides by `2R sin theta sin A sin B sin C`, we get `cot theta - cot B = cot C + cot A` or `cot theta = cot A + cot B + cot C` Squaring both sides, we have `cot^(2) theta = cot^(2) A + cot^(2) B + cot^(2)C + 2(cotA cot B + cot B cot C + cot C cot A)` or `cosec^(2) theta - 1 = (cosec^(2) A -1) + (cosec^(2) B -1) + (cosec^(2) C -1) + 2` [since in `DeltaABC, cot A cot B + cot B cot C + cot C cot A = 1`] or `cosec^(2) theta = cosec^(2) A + cosec^(2) B + cosec^(2)C` Area of triangle ABC, `Delta = Delta_(1) + Delta_(2) + Delta_(3)` `=(1)/(2) [a OB + b OC + c OA] sin theta` `=(1)/(4) tan theta [2 a OB cos theta + 2b OC cos theta+ 2c OA cos theta]` `=(1)/(4) tan theta [(a^(2) + X^(2) -y^(2)) + (b^(2) + y^(2) - z^(2)) + (c^(2) + z^(2) - x^(2)]` `= (1)/(4) tan theta [a^(2) + b^(2) + c^(2)]` |
|
| 3531. |
If S(p,q,r)=(~p)vv[~(q^^r)] is a compound statement, then S(~p,~q,~r) is |
|
Answer» <P>`~S(p,Q,R)` |
|
| 3532. |
Some standard forms of integration : intsinxsqrt(4-cos^(2)x)dx=..........+c |
|
Answer» `-(cosx)/(2)SQRT(4-cos^(2)x)+2log|x+sqrt(4-cos^(2)x)|` |
|
| 3533. |
A tower stands at the foot of a hill whose inclination to the horizon is 9^(@), at a point 40 m up the hill the tower subtends an angle of 54^(@). The height of the tower is |
|
Answer» 17.56 m |
|
| 3534. |
If x^(2)+bx+x=0 has no real roots and a+b+c lt 0 then |
|
Answer» `4a+2b+x GT 0` |
|
| 3535. |
Let a function is defined as f:RtoR such that f(x)=(6)/(1+3"le"^(x)). Find the number of different integral values which function f(x) can take ? |
|
Answer» SOLUTION :f(x) can TAKE 1,2,3,4,5 as f(x) is continous function. `:.` Using IVT we can say that f(x) can take 5 INTEGRAL VALUE 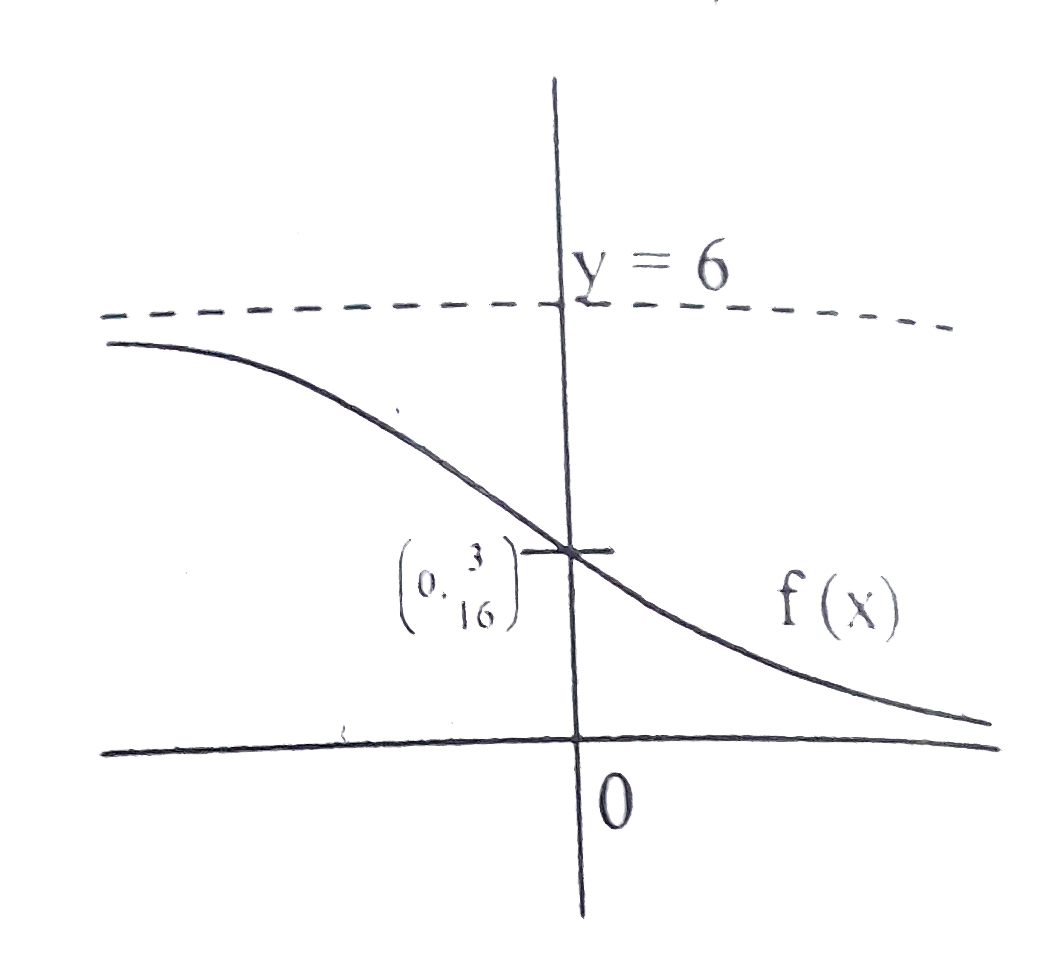
|
|
| 3536. |
If A and B are two events such that P(A)=3/4 and P(B)=5/8, then |
|
Answer» `P(A uu B) ge 3/4` |
|
| 3537. |
A line makes angles of 45^@ and 60^@ with the z-axis and the x-axis respectively. The angle made byit with y-axis is |
| Answer» Answer :B | |
| 3538. |
Findthe areaofthetrianglewhoseverticesare (2,7 ) (1,1),(10 ,8) |
|
Answer» |
|
| 3539. |
Find the magnitude of the vector vec(a)=(3hati+4hatj)xx(hati+hatj-hatk). |
|
Answer» |
|
| 3540. |
Statement -1 :if A = [a_(ij) ]_(nxxn)and a_(ij) =( i^(2) +j^(2) -ij) (I -i) ,T _r (A)= 0. T_r stands for trace ofthe matrix ) Statement -2 A skew symmetric matrix is always non-invertible |
|
Answer» Statement -1 is True ,Statement -2 is True ,Statement -2 is CORECT explanation for Statement -1 |
|
| 3541. |
If the roots of ax^(2) + bx + c = 0 are both positive and b lt 0, then |
|
Answer» `a LT 0, C lt 0` |
|
| 3542. |
A particle moves along the curve y=x^2 + 2x . At what point(s) on the curve are x and ycoordinates of the particle changing at the same rate? |
|
Answer» |
|
| 3543. |
If veca=2hati-hatj+hatk,vecb=3hati+2hatj-3hatk and vecc=hati+2hatj+hatk then 2veca+vecb-vecc= |
|
Answer» `6hati-2hatj-2hatk` |
|
| 3544. |
Study the velocity-time graph pictured below and match each segment of the graph given in list-II with position-time graph given in list-I of this motion at that time. |
|
Answer» P`to`3, Q`to`2,4 , R`to`1 , S`to`6 |
|
| 3545. |
From a point on the ground 100 m away from the base of a building, the angle of elevation of the top of the building is 60^(@). Which of the following is the best approximation for the height of the building ? |
| Answer» ANSWER :B | |
| 3546. |
Let alpha and beta be the roots of equation x^(2) -6x-2=0 if a_(n)=alpha^(n)-beta^(n), for n ge 1, then the value of (a_(10) -2a_(8))/(2a_(9))is equal to |
| Answer» ANSWER :a | |
| 3547. |
If D=[(0,i-100, i-500 ),(100 -i,0,1000-i),(500 -i,i-1000 ,0)]then|D| =…… |
|
Answer» 100 |
|
| 3548. |
A bag contains 5 red balls, 6 green balls and 7 white balls. If three balls are drawn at random, one after another with replacement, then find the probability that these are green, red and white in order. |
|
Answer» |
|
| 3549. |
A lot of 100 watches is known to have 10 defective watches. If 8 watches are selected (one by one with replacement) at random, then what is the probability that there will be atleast one defective watch ? |
|
Answer» |
|
| 3550. |
If A is a square matrix of order 3 such that abs(A)=5, then what is the value of abs(adj(adjA)? |
|
Answer» S. griseus |
|