Saved Bookmarks
Explore topic-wise InterviewSolutions in .
This section includes InterviewSolutions, each offering curated multiple-choice questions to sharpen your knowledge and support exam preparation. Choose a topic below to get started.
| 1651. |
In the given figure, AD is perpendicular to BC and EF || BC, if /_ EAB = /_ FAC, show that triangles ABD and ACD are congruent. Also, find the values of x and y if AB = 2x + 3, AC = 3y + 1, BD = x and DC = y + 1. |
|
Answer» |
|
| 1653. |
The surface area of sphere is1018( 2)/(7) . Sq.cm . What is its volume? |
|
Answer» |
|
| 1654. |
If the mean of the following frequency distribution is 7.2 find value of 'K'. |
|
Answer» |
|
| 1655. |
AB and CD are respectively the smallest and longest sides of a quadrilateral ABCD (see th e given figure). Show that angle A gt angle C and angle B gt angle D |
|
Answer» |
|
| 1656. |
Construct a quadrilateral ABCD with AB=4 cm,BC=2.8 cm, CD=4 cm, angleB=75^(@) and angleC=105^(@). |
|
Answer» Solution :Step 1: Draw a LINE segment AB=4 cm. Step 2: Draw `bar(BX)`, such that `angleABX=75^(@)` Step 3: With B as the center and a radius of 2.8 cm, draw an arc to cut `bar(BX)` at C. Step 4: Draw `bar(CY)` which MAKES an angle `105^(@)` with `bar(BC)`. Step 5: Mark D on `bar(CY)`, such that CD=4 cm. Step 6: JOIN AD, ABCD is the required quadrilateral. 
|
|
| 1660. |
If the mean of observations x,x+2,x+4,x+6 and x+8 is 11, findthe value of x |
|
Answer» |
|
| 1662. |
In the given figure C is the midpoint of AB,D is the midpoint of XY and AC=XD Using an Euclid 's axiom prove that AB =XY |
|
Answer» Solution :We have AB=2AC [`therefore` C is the midpoint of AB] and XY=2xD [`therefore`D is the midpoint of xy] Now AC =XD(given)`rarr` AC=XD(given) `rarr` 2aC=2XD [by EUCLID 's Axiom 6] `rarr`AB =XY [by Euclid 's Axiom 7] HENCE AB XY 
|
|
| 1663. |
A solid sphere with radius 6 cm was totally submerged in water kept in a cylindrical vessel. The water level in the vessel rose by 4.5 cm. Find the radius of the cylindrical vessel. |
|
Answer» |
|
| 1664. |
An Olympic swimming pool isin the shape of a cuboid of dimensions 50m Long and 25 m wide. If it is 3mDeep throughout , how many liters of water does it hold? ( 1cu.m =1000 liters) |
|
Answer» |
|
| 1665. |
Find the volume of a sphere whose radius is (i) 7 cm (ii) 0.63 cm. |
|
Answer» (II) `1.05m^(3)` (APPROX.) |
|
| 1666. |
The radius of sphere is 3.5 cmFind its surface area and volume . |
|
Answer» |
|
| 1667. |
Examine whether the following numbers are rational or irrational : (i)sqrt(5)""(ii)sqrt(9)""(iii)1+sqrt(2)""(iv)2+sqrt(4) (v)sqrt(3)-sqrt(5)""(vi)(2+sqrt(2))^(2)""(vii)(5+sqrt(2))(5-sqrt(2))""(viii)(sqrt(3)-sqrt(2))^(2) |
|
Answer» |
|
| 1668. |
For each of the points given below , checkwhether it is a solution of equation 2x +3y = 24 or not : (6,4) |
|
Answer» |
|
| 1669. |
A sum of Rs 62,000 is divided into three parts such that the corresponding interests earned for 3 years, 5 years and 6 years are equal. If the rates of simple interest are 5% per annum, 4% per annum and 3% per annum, then what is the greatest of the sum that were lens? |
|
Answer» RS 18,000 ii) `(x XX 3 xx 5)/100 = (y xx 5 xx 4)/100 = (([(22,000-(x+y))]6xx3)/100)`. iii) Solve the above equation and find the least of the sums. |
|
| 1670. |
Prove that an equilateral triangle can be constructed on any given line segment. |
Answer» Solution :Let PQ be a line segment of given length. Now, from Euclid's postulate 3, we can draw a circle with centre P and PQ as radius. Similarly, we can draw ANOTHER circle with point Q as centre and QP as radium. These two circles intersect at point R(say). Now, draw the line segments PR and QR to FORM a TRIANGLE PQR.  Now, we have to prove that `DeltaPQR` is equilateral i.e., `PQ=QR=PR` As PQ = PR (radii of the same circle ) ....(1) Similarly PQ = QR (radii of the same circle) .....(2) From eqs. (1) and (2), and Euclid's first axiom which STATES that ''things which are equal to the same thing are equal to the same thing are equal to one another'', we have PQ = QR = PR Hence, `DeltaPQR` is an equilateral triangle. Note Here, without giving any reference, Euclid has assumed that circles drawn with centres as P and Q will meet at a point. |
|
| 1672. |
The mid-value of a class-interval of a frequency distribution is 10 and the class-length of each class is 6, The lower class limit of the class-interval is |
|
Answer» 6 |
|
| 1673. |
If tantheta=cottheta" and "0^(@) le theta le 90^(@), state the value of theta. |
|
Answer» |
|
| 1674. |
Evaluate each of the following using proper identity : 97 xx 103 |
|
Answer» |
|
| 1675. |
The weight (in kg) of seven students are given below: 35, 30, 42, 36, 38, 40, 45 Find the mean weight. |
|
Answer» |
|
| 1676. |
Construct an angle of 90^(@), using ruler and compasses only. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw a RAY `OA`. (ii) With `O` as centre and a conventient radius, draw an arc cutting `OA` at `P`. (iii) With `P` as centre and the same radius as above, draw an arc, cutting the above arc at `Q`. (iv) With `Q` as centre and the same radius, draw another arc, cutting the arc drawn in Step (ii) at the POINT `R`. (v) With `Q` and `R` as CENTRES and the same radius, draw TWO arcs intersecting each other at `M`. (vi) Join `OM` and produce it to point `B`. Then, `angleAOB` is the required angle of measure `90^(@)`. 
|
|
| 1678. |
In the given figure area of IIgm (DEFG) =40 cm^(2), then ar (HDG) + ar (HEF) =? |
|
Answer» `10 cm^(2)` |
|
| 1679. |
According to a census taken towards the end of the year 2009, the population of a rural town was found to be 64,000. The censusauthority also found that the population of this particular town had a growth of 5% per annum. In how many years after 2009 did the population of this town reach 74,088 ? |
|
Answer» |
|
| 1680. |
Shyam had some shares. He sold them at Rs.12 discount. He realized Rs.800 less than what he would have realized if he had sold them at Rs.8 premium. Find the number of shares he sold. |
|
Answer» 40 |
|
| 1681. |
Determine which of the following polynomials has (x +1) as a factor. (i) x ^(3) -x ^(2) -x +1 (ii) x ^(4) - x ^(3) + x ^(2) -x +1 (iii) x ^(4) + 2x ^(3) + 2x ^(2) + x +1 (iv) x ^(3) -x ^(2) - (3- sqrt3) x + sqrt3 |
|
Answer» (II) `(x +1) ^(2) (x-5)` (III) ` (x +1) (x+2) (x+10)` (iv) `(y+1) (y+1) (y-1)` |
|
| 1682. |
Two persons P and Q lent certain amounts at the rate of interest for 2 years and 3 years, respectively, under compound interest. If their final amounts are in the ratio of 3:5, Q's amount at the end of the first year being Rs 8500 and P earned an interest of Rs 510 for the first year, then find the ratio of their principals. |
|
Answer» `33:50` `(P_(1)(1+R/100)^(2))/(P_(2)(1+R/100)^(3))=3/5` `rArr P_(1)/(P_(2)(1+R/100)) = 3/5 rArr I/8500 = 3/5` `rArr P_(1)=5100`. `(P_(1) xx 1 xx R)/(100)=510` `R=10%` `P_(2)(1+R/100)=8500` `rArr P_(2) = 8500 xx 10/11` `rArr P_(2) = 8500 xx 10/11` `therefore P_(1):P_(2) = 5100,8500 xx 10/11` `=3:50/11=33:50`. |
|
| 1683. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 4000","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will need to be replaced before it has covered 4000 km ? |
|
Answer» |
|
| 1684. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 4000","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will need to be replaced after it has covered somewhere between 4000 km and 14000 km ? |
|
Answer» |
|
| 1685. |
A tyre manufacturing company kept a record of the distance covered before a tyre needed to be replaced . The table shows the results of 1000 cases :{:("Distance(in km)","less than 4000","4000 to 9000","9001 to 14000","more than 14000"),("Frequency",20,210,325,445):} If you buy a tyre of this company , what is the probability that : it will last more than 9000 km ? |
|
Answer» |
|
| 1686. |
Check whether the polynomial p (y) = 4y ^(3) + 4y ^(2) -y-1 is a multiple of (2y +1). |
|
Answer» |
|
| 1687. |
The water-tax bills in (in rupee) of 30 houses in a locality are given below: 144,184,130,195,132,134,196,114,212,174,188,210,202,145,175,154,174,178,166,146,135,115,120,114,140,188,179,166,210,208. Construct a frequency distribution table with class size 10. |
|
Answer» Solution :The minimum observation is 114 and the maximum observation is 212. `therefore "RANGE"=(212-114)=98` Class size=10. Since `98 divide 10`=9.8, we should have 10 classes, each of size 10. The class of equal size, CONVERING the above data are: 114-124,124-134,134-144,144-154,154-164,164-174,174-184,184-194,194-204 and 204,214 The FREQUENCY distribution table may be presented as shown below: 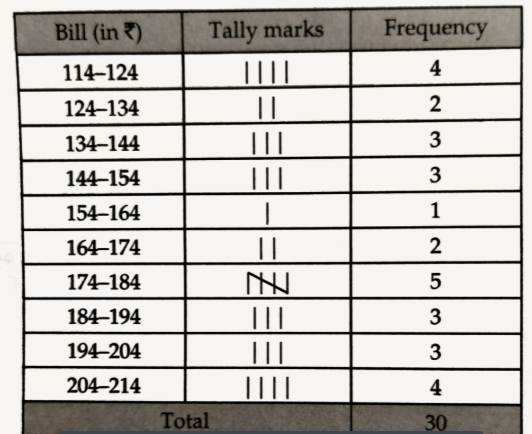
|
|
| 1688. |
Prove that (2)/(sqrt(3)) is irrational. |
| Answer» SOLUTION :N/a | |
| 1689. |
Write each of the following as an equation in two variables : 2x = 3 |
|
Answer» |
|
| 1690. |
Construct an angle of 120^(@), using ruler and compasses only. |
|
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw a RAY `OA`. (ii) With `O` as centre and a CONVENIENT radius, draw a long ARC, cutting `OA` at `P.` (iii) Withas centre and the same radius as above, draw an arc, cutting the previous arc at `Q.` (iv) With `Q` as centre and the same radius, draw YET another arc, cutting the arc drawn in Step (ii) at `R.` (v) Join `OR` and PRODUCE it to a point `B.` Then, `angleAOB` is the required angle of measure `120^(@)`. 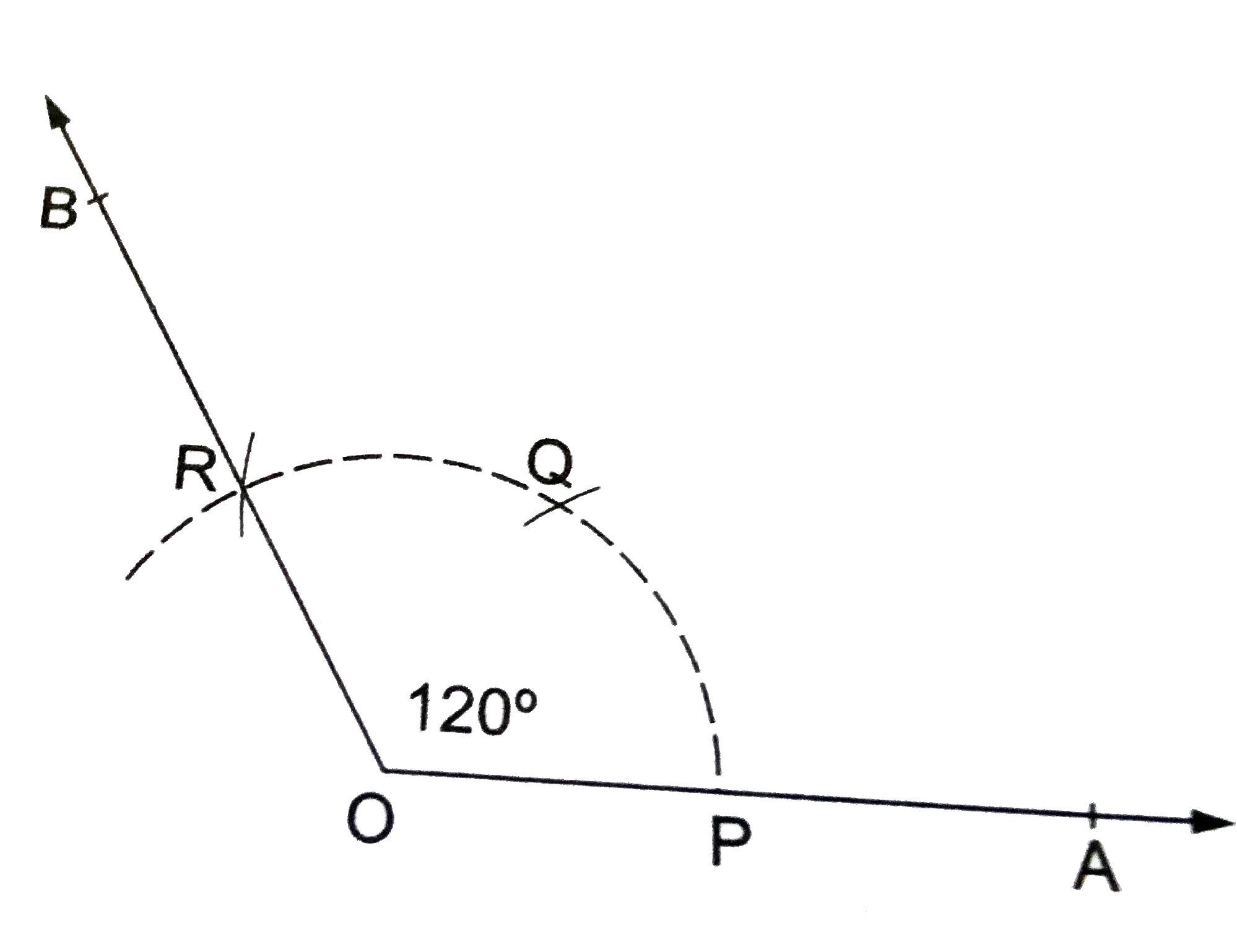
|
|
| 1691. |
Check whether 2t + 1 is a factor of 4t^(3) + 4t^(2) - t - 1 or not. |
|
Answer» |
|
| 1692. |
Factorise : 2x^(3) + 7x^(2) + 2x -3 |
|
Answer» |
|
| 1693. |
Fill in the blands so as to make each of the following statements true : The longest chord of a circle is its …….. |
|
Answer» |
|
| 1694. |
Centuries scored and number of cricketers in the world are given below. Find the mean, median and mode of the given data. |
|
Answer» |
|
| 1695. |
Construct a DeltaABC whose perimeter is 14 cm and sides are in the ratio 2 : 3 : 4. |
|
Answer» Solution :Steps of construction : 1. DRAW a line segment `PQ = 14 cm.` 2. Draw a ray `PX,` making an acute angle with `PQ`and drawn in the downward direction. From `P,` set off `(2+3+4) = 9` equal DISTANCES along `PX.` Mark points `L, M, N` on `PX` such that `PL = 2` units, `LM = 3` units and `MN = 4` units. 5. JOIN `NQ.` Through `L` and `M,` draw `LB` `||` `NQ` and `MC` `||` `NQ`, cutting `PQ` at `B` and `C` respectively. 7. With `B` as centre and radius `BP,` draw an arc. 8. With `C` as centre and radius `CQ,` draw another arc, cutting the previous arc at `A.` Join `AB` and `AC.` Then, `DeltaABC` is the required triangle. 
|
|
| 1696. |
If two negative integersn_1 and n_(2)be such thatn_2 ne -1 , n_(2)ne -2 and -3< n_(v) ,n_(2) < 3then find the values of |
|
Answer» `n_(1) + n_(2) ` |
|
| 1697. |
Shanti Sweet Stall was placing an order for making carboard boxes for packing their sweets. Two sizes of boxes were required. The bigger of dimensions 25cm xx20cm xx5cm and the smaller of dimensions15cm xx 12cm xx5cm. For all the overlaps, 5% of the total surface area is required extra. If the cost of the carboard is Rs. 4 for 1000 cm^(2), find the cost of carboard required for supplying 250 boxes of each kind. |
|
Answer» |
|
| 1698. |
State true or false .The region enclosed by a chord and the major arc is major segment |
|
Answer» |
|
| 1699. |
Construct a quadrilateral ABCD in which AB=4.2 cm, angleA=80^(@), BC=2.4 cm, CD=3.3 cm and AD=2.4 cm. |
|
Answer» Solution :Step 1: Draw a LINE segment AB=4.2 cm. Step 2: Draw `angleBAX=80^(@)`. Step 3: Mark D on `bar(AX)`, such that AD=2.4 cm. Step 4: Taking D as the center and 3.3 cm as the radius, draw an arc, and taking B as the centre and 2.4 cm as radius, draw another arc to intersect the PREVIOUS arc at C. step 5: Join CD and BD. ABCD is the REQUIRED quadrilateral. 
|
|