InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
A road roller of 200 kg wt slides on ground when pushed by a lever AB of length 1m, as shown in the figure. The force required to slide the roller acts at a distance of 5cmfrom the fulcrum. If the coefficient of friction between the roller and the ground is sqrt(2) find the effort required to move the roller. (Takeg= 10 m s^(-2)) |
|
Answer» Solution :The VARIOUS forces acting on the road roller are shown below in figure. Let the force required to slide the roller be F. The component of the force F, to overcomethe force of friction `f_(s)` is `F cos theta = F cos theta 45^(@)=(F)/(sqrt(2)) " " (1)` 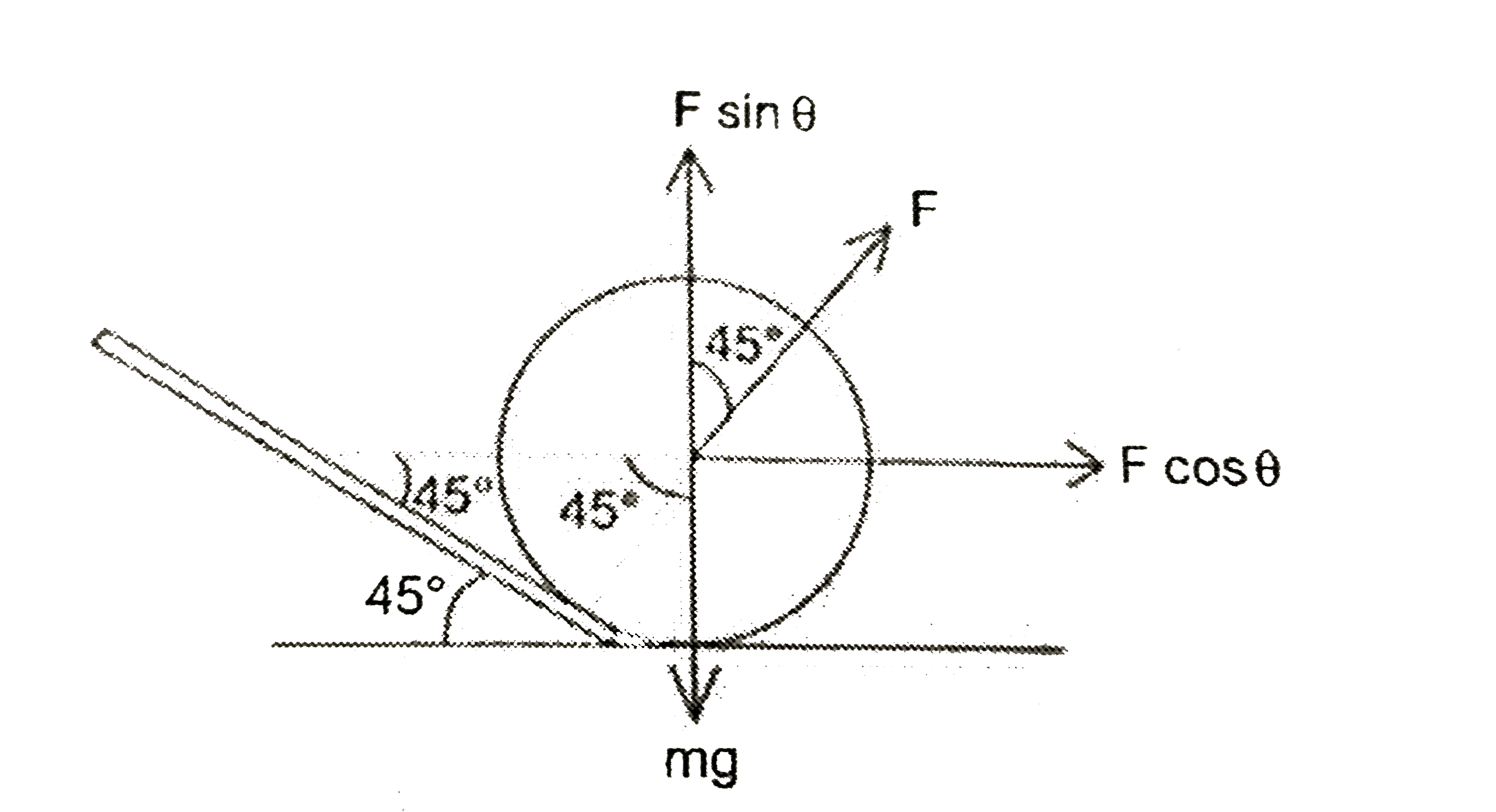 The force of friction `f_(s)= mu N ` where` N = mg - F sin theta` substituting mg`=200xx10=2000 N` ` sin theta = sin = 45^(@)` `N= 2000 -(F)/(sqrt(2))` The frictionalforce `f_(s)` `f_(s)= mu N = sqrt(2)xx(200-(F)/(sqrt(2)))` `f_(s)=2000 sqrt(2)-F "" (2)` Equationg (1) and (2) `(F)/(sqrt(2))=2000 sqrt(2)-F` `F=4000-sqrt(2)F` `F=(4000)/(sqrt(2)+1)=(4000)/(sqrt(2)+1)xx(sqrt(2)-1)/(sqrt(2)-1)` `=4xx414=1656N` Applyingthe lawof MOMENTS to the lever, E `xx` EFFORT arm = load `xx` load arm `Exx1= 1656 xx 0.05` `E=82.8 N ~= 83 N` (approximately) |
|