InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
A tailor stiches trousers and shirts and each piece is completed by two machine I and II. To complete each trousers, machines I and IImust work 3/2 hours and 2 hours respectively, and to complete each shirt, machines I and II must work 2 hours and 1 hours respectively Machine I may not operate for more than 12 hours ped day and machine II not more than 11 hours per day. If the profit on each trouser and eachshirt is Rs. 150 and Rs. 100 repectively, then the maximum profit is _______ |
|
Answer» RS. 900 Let the number of shirts=y 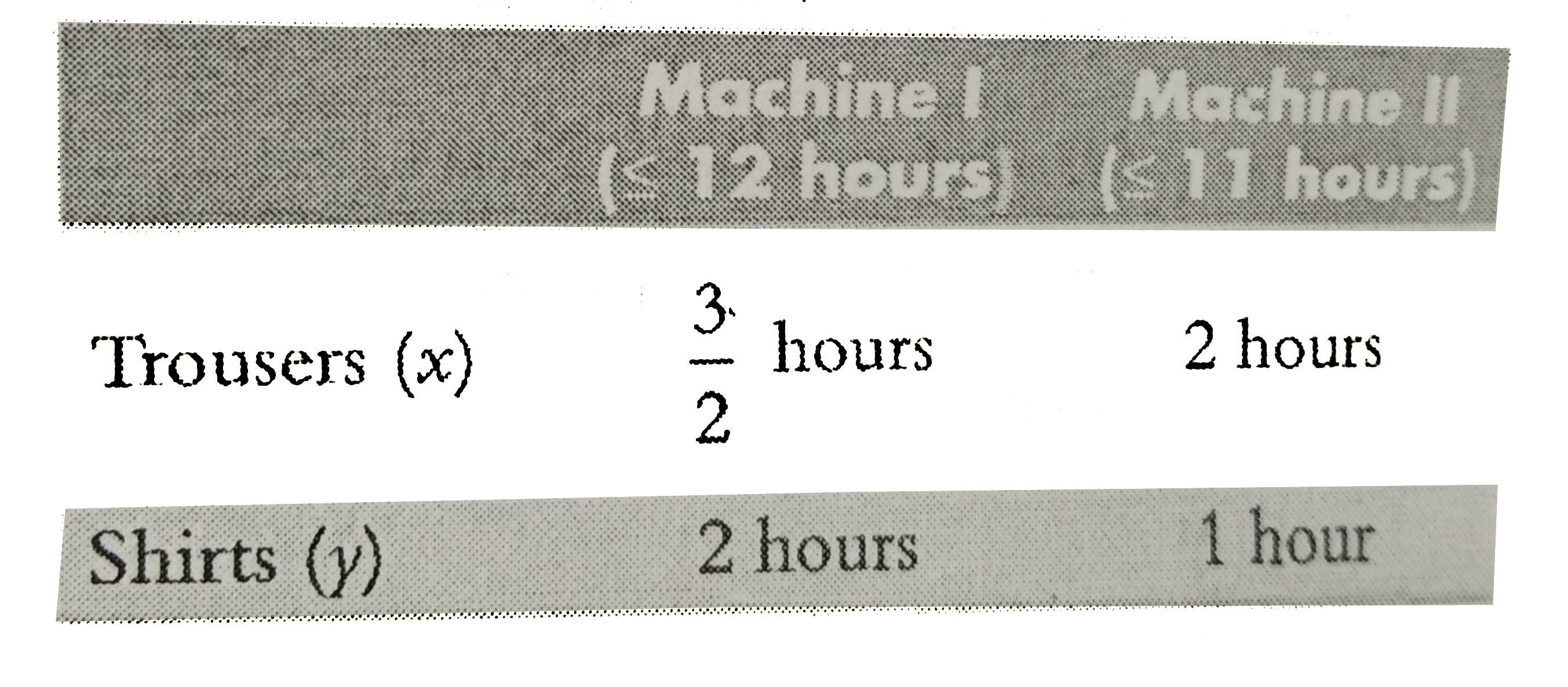 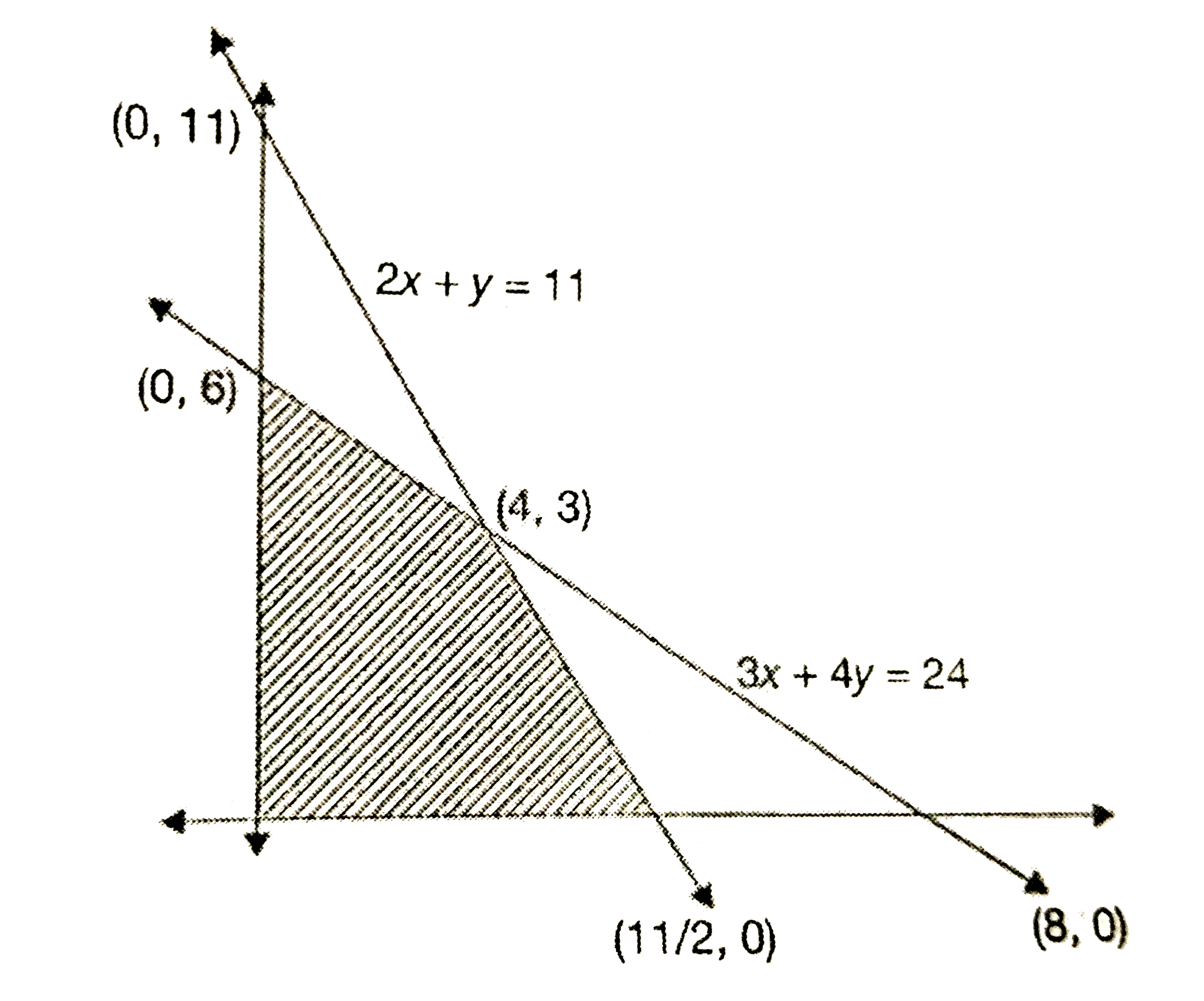 According to the given condition : `implies (3x)/(2)+2y LE 12 and 2x+y le 11` `implies 3x+4y le24 and 2x+y le 11` `x ge 0, y ge 0` The profit function , p=15x+10y The shaded region is a closed- convex polygon with vertices `((11)/(2),0),(4,3),(0,6),(0,0).` `:.` ABCD is the feasible reason. `:.` THe maximum profit is at C(4,3), i.e., `P=150xx4+100xx3=900.` |
|