Saved Bookmarks
| 1. |
An object is kept on the principal axis of a concave mirror of focal length 12 cm. If the object is at a distance of 18 cm from the mirror, calculate the image distance. Determine the nature of the image formed by calculating the magnification produced by the mirror. |
|
Answer» Solution :Concave mirrorf = 12 cm focal length = 12 cm Object distance = 18 cm Nature of image = ? Formula : `(1)/(f) = (1)/(U) + (1)/(v)` `(1)/(v) = (1)/(f) - (1)/(u)` `(1)/(v) = (1)/(-12) - (1)/(18)` `(1)/(v) = -(1)/(12) + (1)/(18)` `(1)/(v) = - (1)/(36)` v = - 36 (real image in front of mirror ) magnification = - `(1)/(v)` = - `((-36))/(18)` = + 2 (upright ) Nature of iimage : Real and upright image OR Power = -0.5 D nagetive sign means : MYOPIA or short sightedness Power = `(1)/(f)` f = `(1)/(-0.5) = - (10)/(5) = -2.0 m xx 100` = - 200 cm Concave lens (diverging lens) In myopia, eye is unable to view long distance objects. The image in this case falls before the retina. For every myopic eye, there exists a far point beyond which clear image cannot be seen. The short-sightedness(myopia) is corrected by using a concave lens which diverges and shifts the image to the retina. 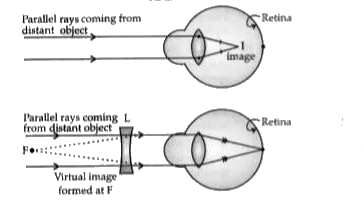
|
|
Discussion
No Comment Found
Related InterviewSolutions
- What is the name given to a pure substance with only one kind of atoms?
- What is the difference between pure gold and 22 carat gold? Which type of gold is used for making ornaments ?
- The term pH was coined by ______
- Write the formula of the product formed when the element A (atomic number 19) combines with the element B (atomic number 17). Draw its electronic dot structure. What is the nature of the bond formed?
- Which of the following metal is not found in a free state ?
- Why are alcohols poor conductors of electricity ?
- Which one of the following element is used as the standard for measuring the relativeatomic mass of an element in now a days?
- The thickness of _______ increases in the electrorefming of copper
- What do you think would happen when a mixture of iron filings and sulphur powder is heated ?
- What is the formula of the next homologue of propene (C_3H_6)?