Construct a Delta ABC whose perimeter is 12 cm and the base angles are 60^(@) and 70^(@). Justify the construction.

Construct a Delta ABC whose perimeter is 12 cm and the base angles are

1.	Construct a Delta ABC whose perimeter is 12 cm and the base angles are 60^(@) and 70^(@). Justify the construction.
Answer» Solution :STEPS OF CONSTRUCTION (i) Draw a line segment `PQ=12` CM. (II) Make `angleQPR=60^(@)` and `anglePQS=70^(@)`. (iii) Draw the bisectors of `angleQPR` and `anglePQS` to meet at`A`. (iv) Draw the perpendicular bisectors of `PA` and `QA` to meet `PQ` at `B` and `C` respectively. (v) JOIN `AB` and `AC`. Then, `Delta ABC` is the required triangle. 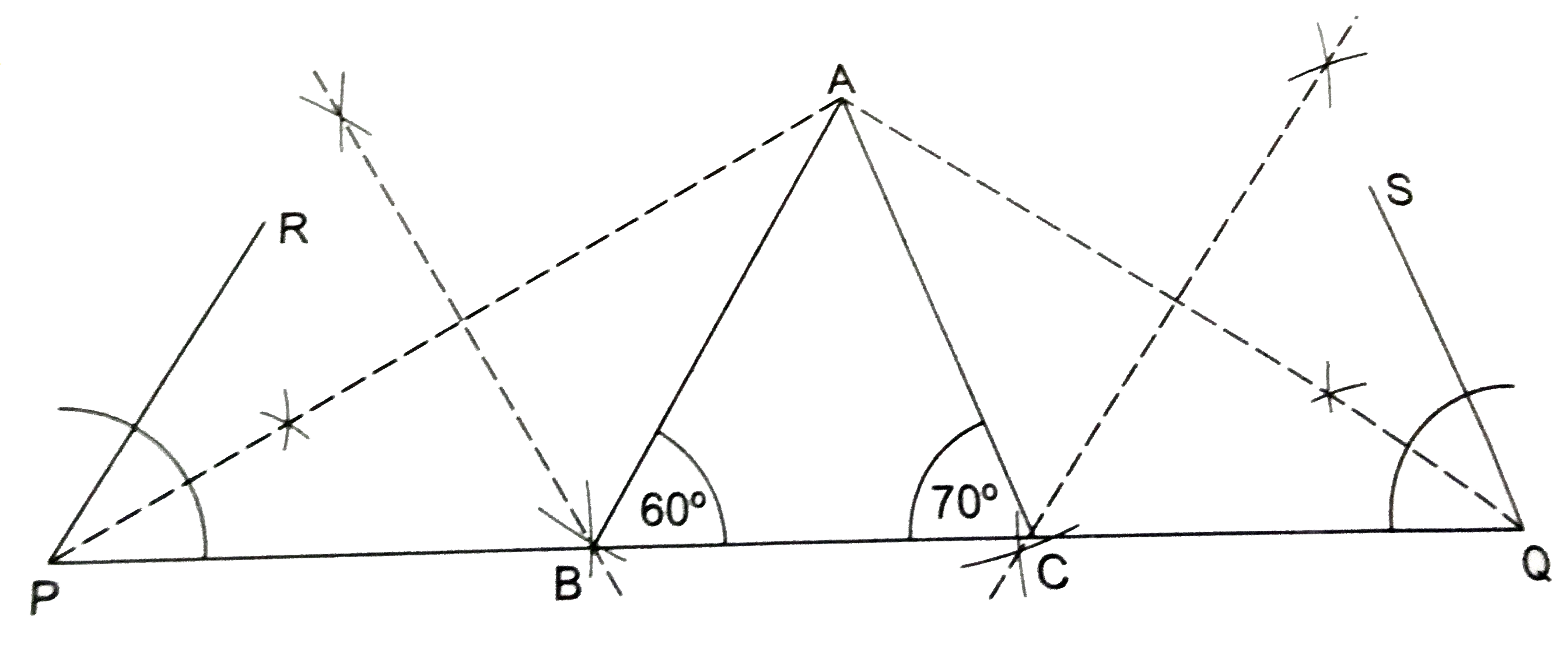Justification : Since `B` lies on the perpendicular bisector of `AP`, we have `BA=BP`. Since `C` lies on the perpendicular bisector of `AQ`, we have `CA=CQ`. Thus, `AB=PB` and `AC=CQ`. `:. AB+BC+AC=PB+BC+CQ=PQ=12` cm. Now, `BA=BP implies angleBPA=angleBAP` `implies angleABC=angleBPA+angleBAP=2 angleBPA` `=2xx1/2xx60^(@)=60^(@)`.And, `CA=CQ implies angleCQA=angle CAQ` `implies angleACB=angleCQA+angleCAQ=2angleCQA` `=2xx1/2xx70^(@)=70^(@)`. Verification : On measurement, we find that `AB+BC+CA=(4.4+3.5+4.1) cm =12` cm. `angleB=60^(@)` and `angleC=70^(@)`.