InterviewSolution
Saved Bookmarks
| 1. |
Construct an isosceles triangle whose base in 8 cm and altitude 4 cm and then another triangle whose sides are 1(1)/(2) times the corresponding sides of the isosceles triangle. |
|
Answer» Solution :Setps of Construction : 1. Draw line segment BC = 8 CM. 2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P. 3. Along PO cut off PA = 4 cm. 4. Join BA and CA. So, `DeltaABC` is the required isosceles triangle. 5. From B, draw any ray BX making an acute `ANGLECBX`. 6. Locate three points `B_(1),B_(2)and B_(3)` on BX such that `BB_(1)=B_(1)B_(2)=B_(2)B_(3).` 7. Join `B_(2)C` and from `B_(3)` draw a line `B_(3)N"||"B_(2)C` intersecting the extended line segment BC at N. 8. From point N, draw `NM"||"CA` meeting MA produced at M. Then, `DeltaMBN` is the required triangle. Justification : `because""B_(3)N"||"B_(2)C""("by construction")` `therefore""(BN)/(BC)=2/1` `Now,""(BN)/(BC)=(BC+CN)/(BC)=1+(CN)/(BC)=1+1/2=1(1)/(2)` 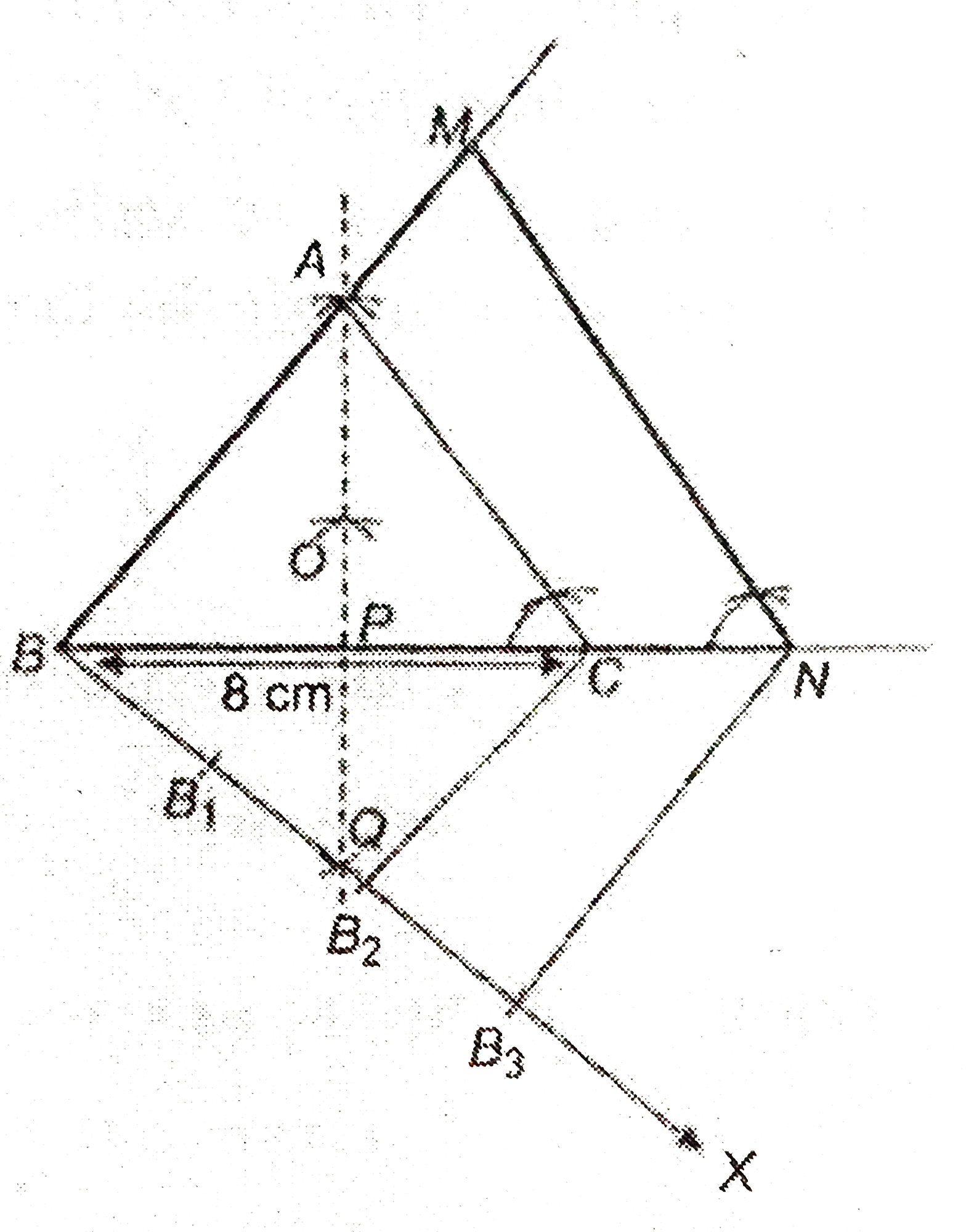
|
|