"Derive"(1)/(R)=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3)).

1.	"Derive"(1)/(R)=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3)).
Answer» Solution :Parallel CONNECTION : In Parallel connection of resistors there is same potential difference at the ends of the resistors. Hence the voltage in the CIRCUIT is equal to V. Let `I_(1),I_(2)andI_(3)` be the currents flowing through `R_(1),R_(2)andR_(3)` resistors respectively. Hence, we can write `I=I_(1)+I_(2)+I_(3).` According to the Ohm's law. `V_(1)=1_(1)R_(1),V_(2)=I_(2)R_(2),V_(3)=I_(3)R_(3)` here,`V=V_(1)=V_(2)=V_(3)` `thereforeV=I_(1)R_(1),V=I_(2)R_(2),V=I_(3)R_(3)` `rArrI_(1)=(V)/(R_(1)),I_(2)=(V)/(R_(2))andI_(3)=(V)/(R_(3))` `thereforeI=I_(1)+I_(2)+L_(3)` `rArr(V)/(R_(eq))=(V)/(R_(1))+(V)/(R_(2))+(V)/(R_(3))` `rArrcancel(V)xx(1)/(R_(eq))=cancel(V)[(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))]` `rArr(1)/(R_(eq))=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))(" here " R_(eq)" is the equivalent resistance ")` `therefore` The equivalent resistance of a parallel combination is LESS than the resistance of each of the resistors.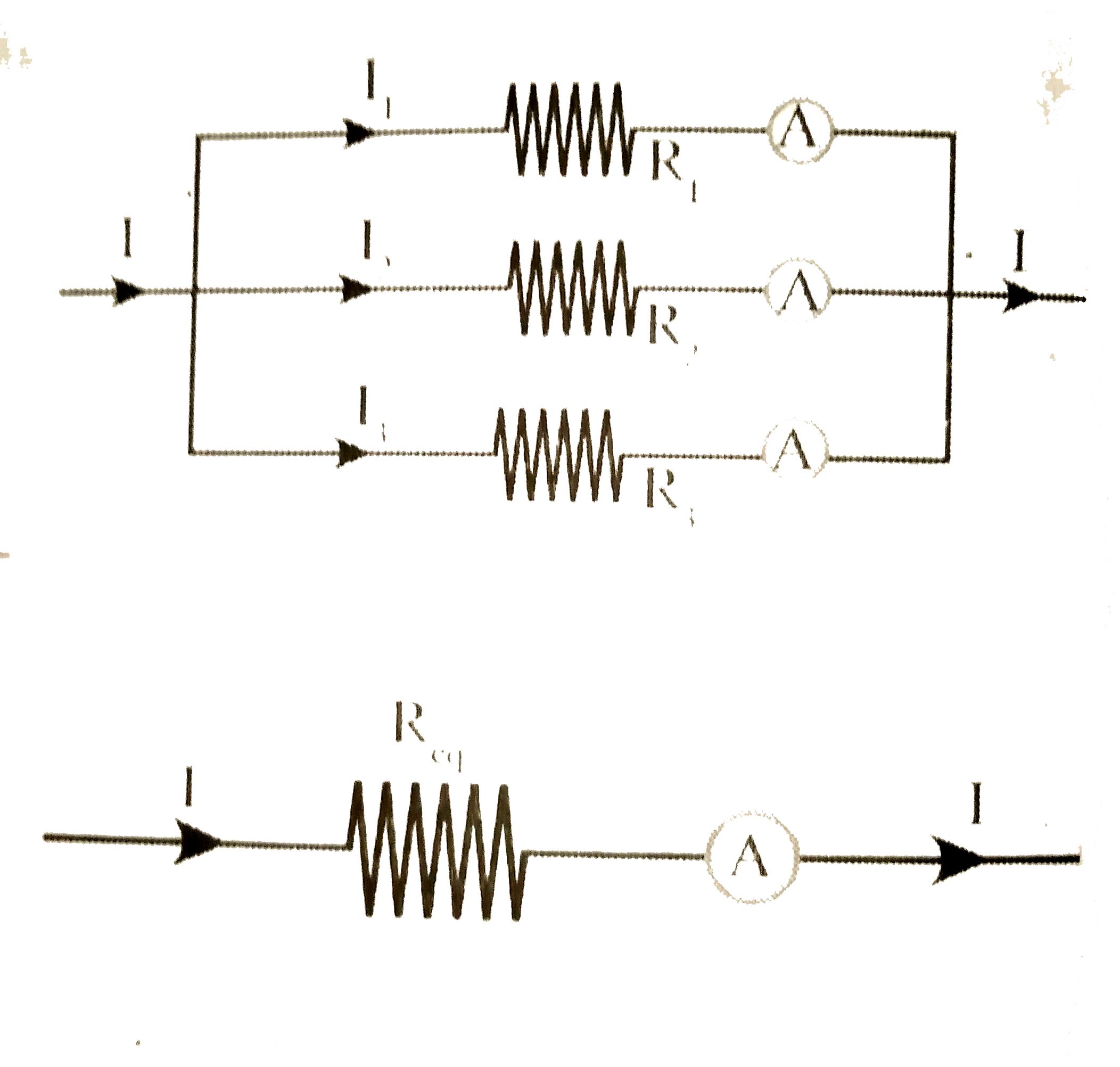

Discussion