Derive an expression for the effective resistance when three resistors are connected in (i) series (ii) parallel.

Derive an expression for the effective resistance when three resistors

1.	Derive an expression for the effective resistance when three resistors are connected in (i) series (ii) parallel.
Answer» Solution :PARALLEL Connection : In Parallel connection of resistors there is same potential difference at the ends of the resistors. HENCE the voltage in the circuit is EQUAL to V. Let `I_(1),I_(2)andI_(3)` be the currents flowing through `R_(1),R_(2)andR_(3)` resistors respectively. Hence, we can write `I=I_(1)+I_(2)+I_(3).` According to the Ohm's law. `V_(1)=1_(1)R_(1),V_(2)=I_(2)R_(2),V_(3)=I_(3)R_(3)` here,`V=V_(1)=V_(2)=V_(3)` `thereforeV=I_(1)R_(1),V=I_(2)R_(2),V=I_(3)R_(3)` `rArrI_(1)=(V)/(R_(1)),I_(2)=(V)/(R_(2))andI_(3)=(V)/(R_(3))` `thereforeI=I_(1)+I_(2)+L_(3)` `rArr(V)/(R_(eq))=(V)/(R_(1))+(V)/(R_(2))+(V)/(R_(3))` `rArrcancel(V)xx(1)/(R_(eq))=cancel(V)[(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))]` `rArr(1)/(R_(eq))=(1)/(R_(1))+(1)/(R_(2))+(1)/(R_(3))(" here " R_(eq)" is the equivalent resistance ")` `therefore` The equivalent resistance of a parallel combination is less than the resistance of each of the resistors.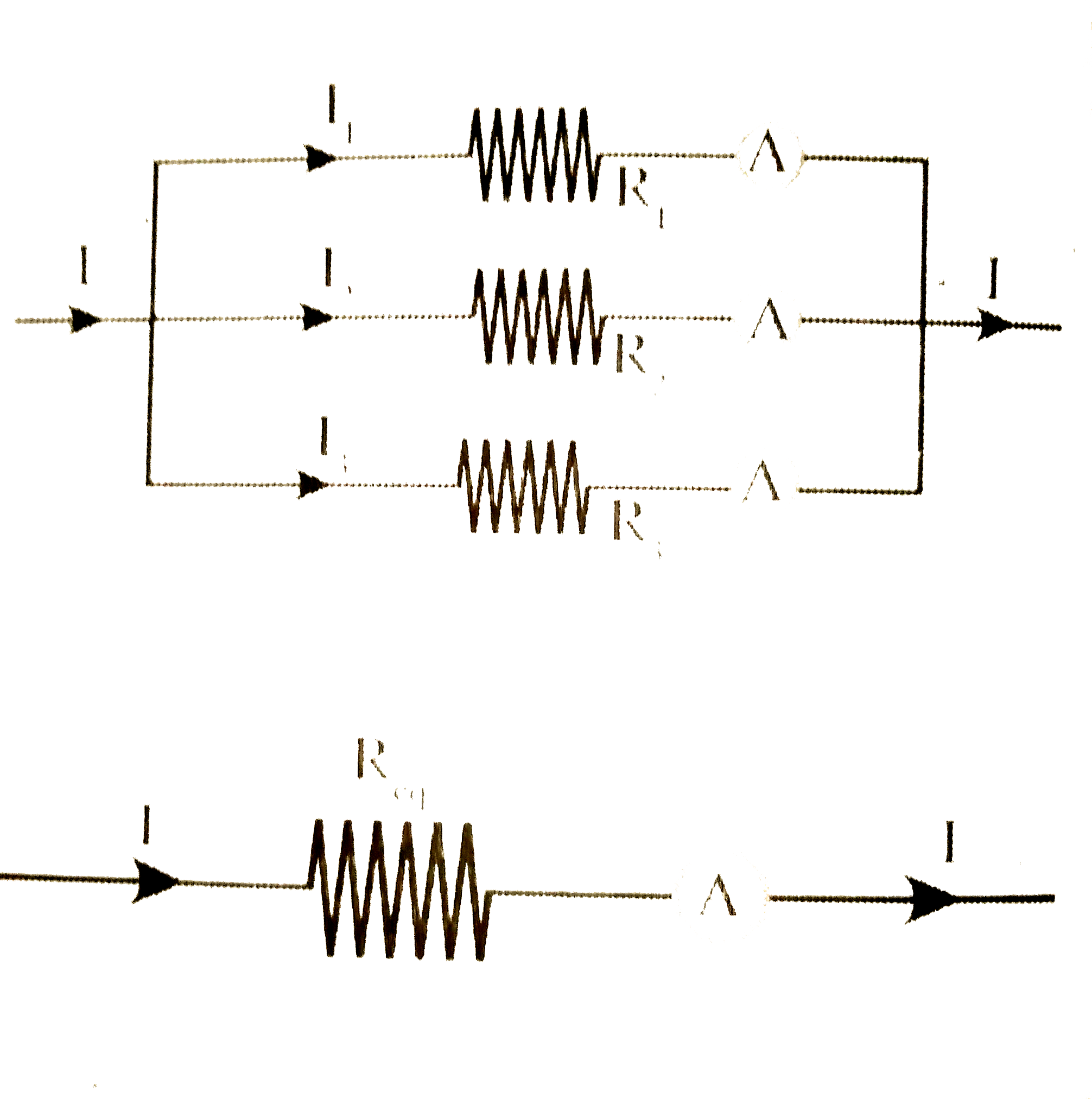