InterviewSolution
Saved Bookmarks
| 1. |
Derive an expression for the pressure of an ideal gas in a container from Kinetic Theory and hence give Kinetic Interpretation of Temperature. |
Answer» Solution :Consider a cube of side .l. and an ideal GAS is filled in it. Let the co-ordinates, X, Y and Z will coincide with the sides of the cube. Let velocities of gas molecules along these directions are `V_(x), V_(y) and V_(z)`. Consider a gas molecule moving along X-axis with a velocity `V_(x)`. Its motion is perpendicular to Y-Zplane. Let the gas molecule SUFFERED elastic collision with Y-Z planeand bounced back. In this case the velocities `V_(y) and V_(z)` are not considered because collision is along X-direction only. 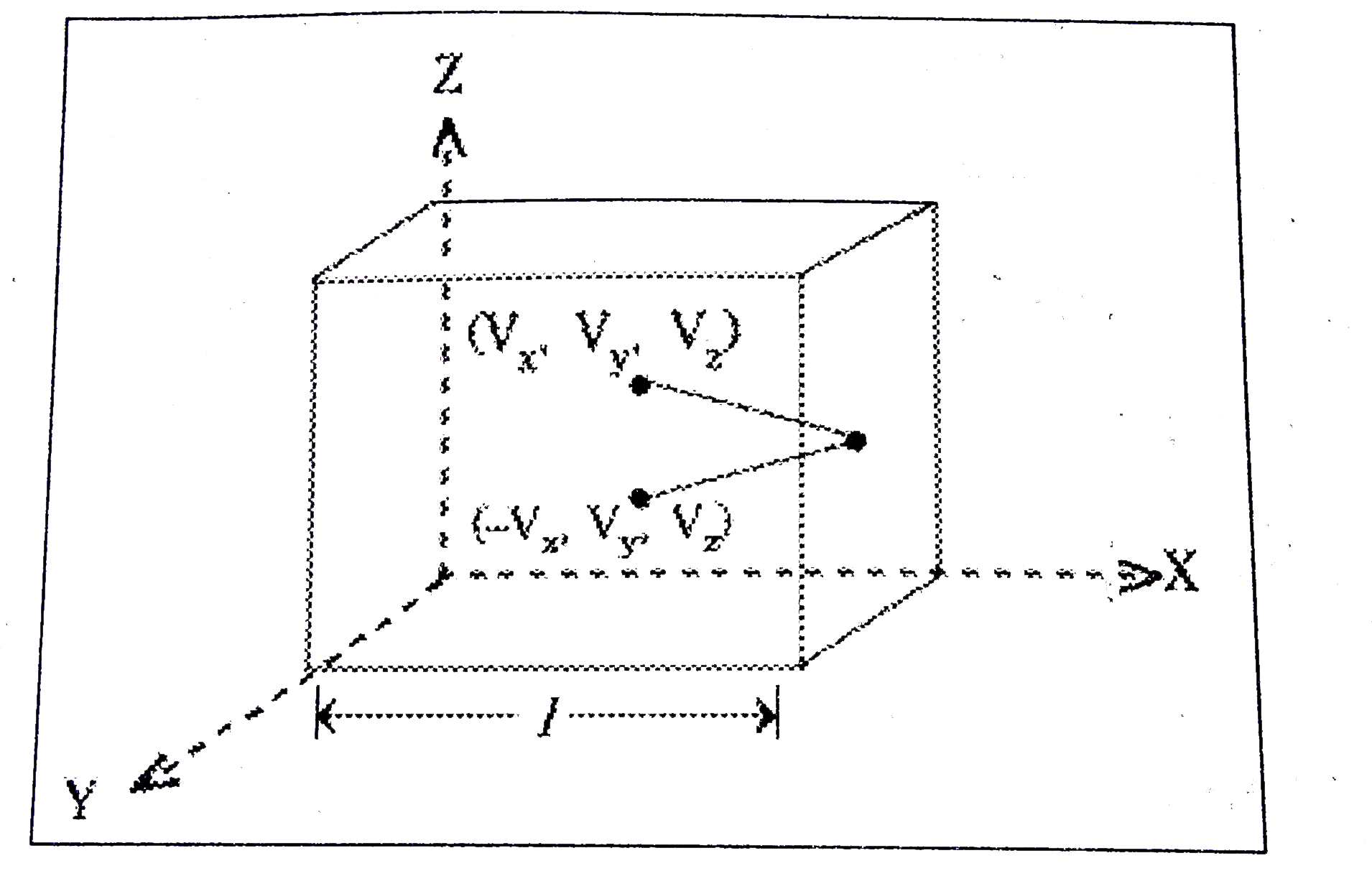 Change in MOMENTUM along X-direction is final momentum `(-mV_x)` - initial momentum `(mV_x) = -2mV_(x)` ...........(1) Let area of one side of the cube is A. Then during the time `Delta t` only the molecules at a distance of `V_(x) Delta t` will collide with the walls. Let number of gas molecules in the volume `AVDelta t` are say.n.. In these molecules half of the molecules will move towards the wall and remaining will move away from the wall. `:.` Amount of momentum transferred to the wall = Q `= 2mV_(x) xx` number of molecules collided with wall `:. Q = 2mV_(x) (1/2 nAV_(x)Delta t)` Pressure on Y - Z plane = `P_(x) = ("Rate of change in momentum")/("Area")` `:. P = ("Force")/("Area") = (Q//Delta t)/(A)` `= (2mV_(x).1/2 nAV_(x)Deltat)/(A Delta t) = nmV_(x)^(2)` If behaviour of gas is isotropic that is equal in all directions then `V_(x) = V_(y) = V_(z)` `:.` Root mean square velocity of gas `=(V_(x)^(2)+V_(y)^(2)+V_(z)^(2))/(3) = 1/3 bar(V)^(2)` Where `bar(V)^(2) = V_(x)^(2) + V_(y)^(2) + V_(z)^(2)` `:.` Pressure of gas `P = 1/3 nmbar(V)^(2)` From Pascal.s law pressure is same throught the container so pressure in any direaction (say x,y or z) is same. Kinetic interpretation of temperature : From gas equation `PV = 1/3 nmbar(V)^(2) . V = 2/3 N (1/2) mbar(V)^(2))` Where `N = nV` and `1/2 mbar(V)^(2)` = kinetic energy for ideal gas internal energy is purely kinetic energy. `:. E = n 1/2 mbar(V)^(2) :. PV = 3/2 E` But `P = K_(B)NT` `:. E = 3/2 PV = 3/2 K_(B)N.T` But `E/N = 1/2 mV^(2) and E/N = 3/2 K_(B)T` `:. E/N alpha T` is the average kinetic energy of gas molecule is proportional to absolute temperature of gas. But it does not DEPEND on volume of container. 
|
|