InterviewSolution
Saved Bookmarks
| 1. |
Draw a neat labelled diagram of Hope's apparatus. Explain how this apparatus can be used to demonstrate anomalous behaviour of water.Drawa graph of temperatureof water against time. |
|
Answer» Solution :Figure shows Hope's apparatus. Initially, the cylindrical container in Hope'sapparatus is filled with water at about `12^(@)C `and the flat bowl is filled with a freezing mixture of ice and salt. The temperature of water in the upperpart of the container `( T_(2))` is recorded by thermometer `T_(2)`and that of water in the lower part of the container `( T_(1))` is recorded by thermometer `T_(1)`. Figure shows variation of temperature of water with time. Initially, both the thermometers show the same temperature(say,`12^(@)C)`. In a short time, the temperature shown by the lower thermometer starts decreasing, while the temperature shown by the upper thermometer does not change very much. This process continues till the temperature till the temperature shown by the lower thermometer falls to `4^(@)C ` and remains CONSTANT THEREAFTER . This shows that in the temperature range `12^(@)C ` to `4^(@)C`, density of the water in the central part of the container goes on increasing and hence the water sinks to the bottom.It means that water contracts, i.e., its volume decreases as its temperature falls from `12^(@)C ` to `4^(@)C`. 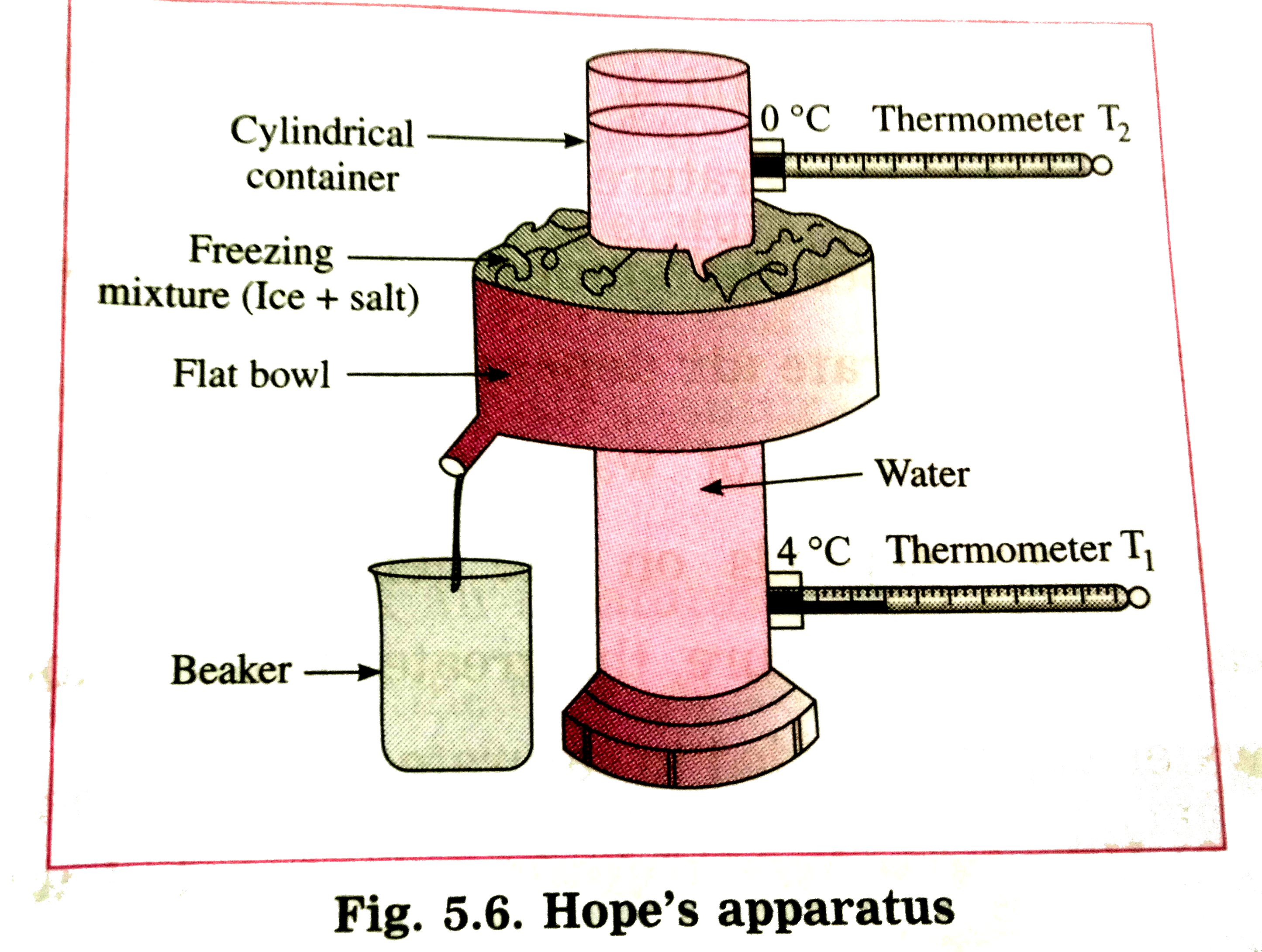 Asthe temperature of the water in the central part of the container becomes less than `4^(@)C `, the temeprature shown by the upper thermometer beings to fall rapidelyto `0^(@)C`. But the temperature shown by the lower the thermometer remains constant `( 4^(@)C)` . Later, the reading shown by the lower thermometer decreases to `0^(@)C `. In the temperature range `4^(@)C ` to `0^(@)C ` , the water moves upward. This shows that the denisty of water goes on decreasing in this range. It means that water expands, i.e., its volume increasesas its temperature falls from `4^(@)C ` to `0^(@)C`. Thus, the volume of a given mass of water is minimum at `4^(@)C ` , i.e., the density of water is maximum at `4^(@)C `.  In figure, the POINT of INTERSECTION of the two curves shows the temperature at which the density of water is maximum .This temperature is `4^(@)C`. |
|