InterviewSolution
Saved Bookmarks
| 1. |
Draw an isosceles triangle ABC in which AB=AC= 6 cm and BC=5 cm. Construction a triangle POR similar to DeltaABC in which PQ=8 cm. Also justify the construction. |
|
Answer» Solution :Let `DeltaPQR` and `DeltaABC` are similar triangles, the its scale factor between the corresponding sides is `(PQ)/(AB)=(8)/(6)=(4)/(3)`. STEPS of construction 1. Draw a LINE segment BC=5cm. 2. Construct OQ the perpendicular bisector of line segment BC meeting BC at P'. 3. Taking B and C as centre draw TWO arcs of equal radius 6 cm intersecting each other at A Join BA and CA. So., `DeltaABC` is the required isosceles triangle 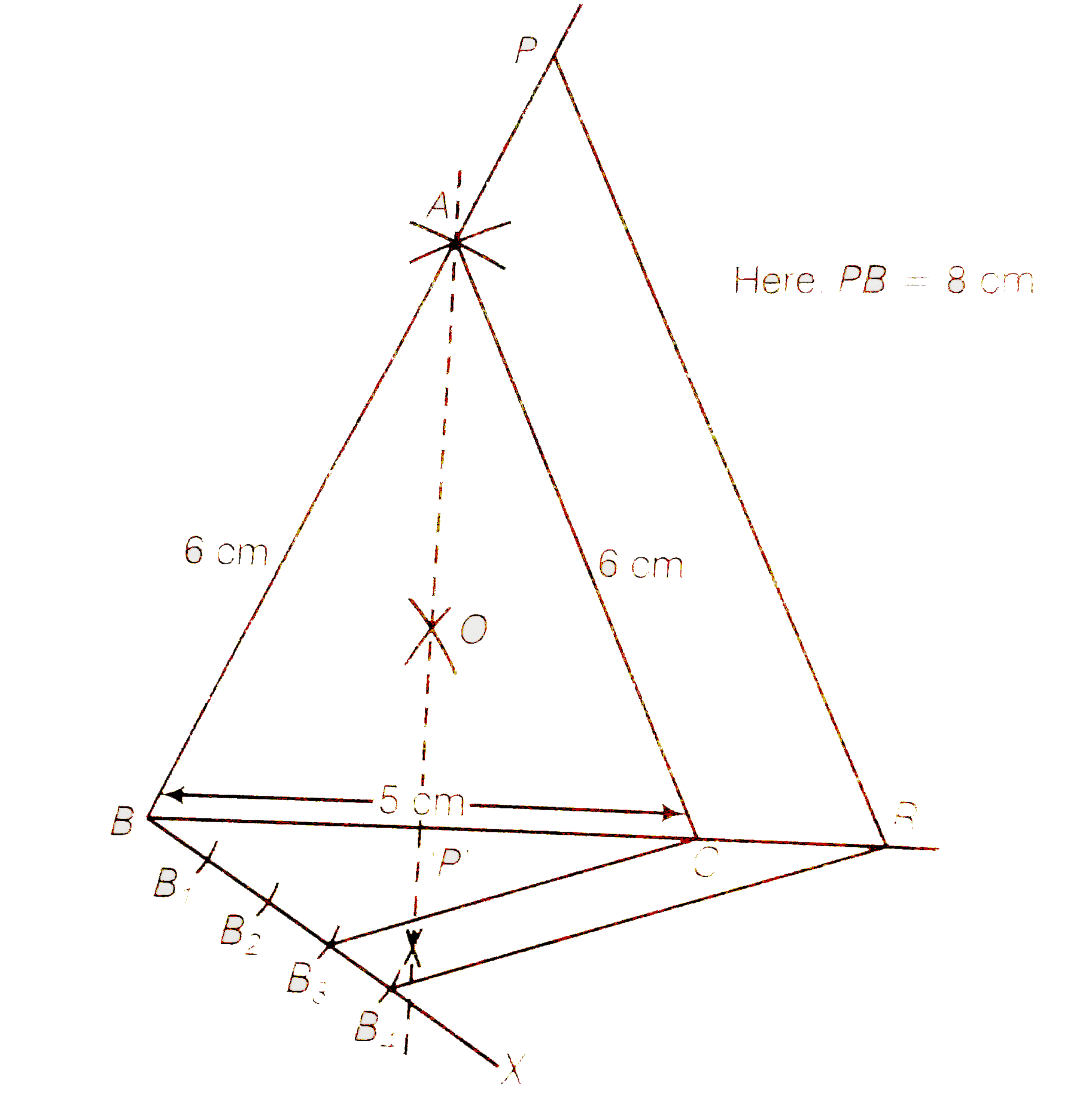 5 From, draw any ray BX making an acute `angleCBX`. 6. Locate four points `B_(1),B_(2),B_(3) " and " B_(4)` on BX such that `BB_(1)=B_(1)B_(2)=B_(2)B_(3)=B_(3)B_(4)`. Join `B_(3)C` and from `B_(4)` draw a line `B_(4)R||B_(3)C` intersecting the extended line segment BC at R. 8. From point R, draw `RP||CA` meeting BA produced at P. Then `DeltaPBR` is the required triangle. Justification `:. B_(4)R||B_(3)C` ( by construction ) `:. (BC)/(CR)=(3)/(1)` `Now, (BR)/(BC)=(BC+CR)/(BC)` `=1+(CR)/(BC)=1+(1)/(3)=(4)/(3)` Also, RP||CA `:. DeltaABC ~ DeltaPBR` and `(PB)/(AB)=(RP)/(CA)=(BR)/(BC)=(4)/(3)` Hence, the new triangle is similar to the given triangle whose sides are `(4)/(3)` times of the corresponding sides of the isosceles `DeltaABC`. |
|