Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R_(1), R_(2) and R_(3) connected In series. Calculate the equivalent resistance of the combination of three resistors of 2 Omega, 3 Omega and 6Omega joined in parallel.

Establish a relationship to determine the equivalent resistance R of a

1.	Establish a relationship to determine the equivalent resistance R of a combination of three resistors having resistances R_(1), R_(2) and R_(3) connected In series. Calculate the equivalent resistance of the combination of three resistors of 2 Omega, 3 Omega and 6Omega joined in parallel.
Answer» Solution :An applied potential V PRODUCES current I in the resistors `R_(1),R_(2)`and `R_(3)`, causing a potential drop `V_(1)V_(2)` and `V_(3)` respectively through each resistor.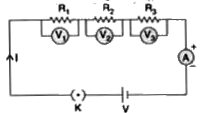 Total Potential `, V = V_(1) +V_(2) +V_(3)` By Ohm.s Law `V_(1) =IR_(1)` `V_(2)= IR_(2)` `V_(3)=IR_(3)` THUS `V=IR_(1)+IR_(2)+IR_(3)` `=I(R_(1)+R_(2)+R_(3))` IF R is the equivalent resistance `V=IR ` Hence `IR = I(R_(1)+R_(2)+R_(3))` `R=R_(1)+R_(2)+R_(3)` This proves that overall resistance increases when resistors are connected in series. Three resistors `2 OMEGA, 3 Omega`and `Omega`, are joined in parallel combination. Equivalent resistance `(1)/(R_(p))=(1)/(2)+(1)/(3)+(1)/(6)` `= (2+2+1)/(6) =(6)/(6)` `R_(p)= 1Omega`