InterviewSolution
Saved Bookmarks
| 1. |
Find k so that x^(2)+2x+k is a factor of 2x^(4)+x^(3)-14x^(2)+5x6. Also find all zeroes of two polynomials. |
|
Answer» <P> and `"" g(x)=x^(2)+2x+k` 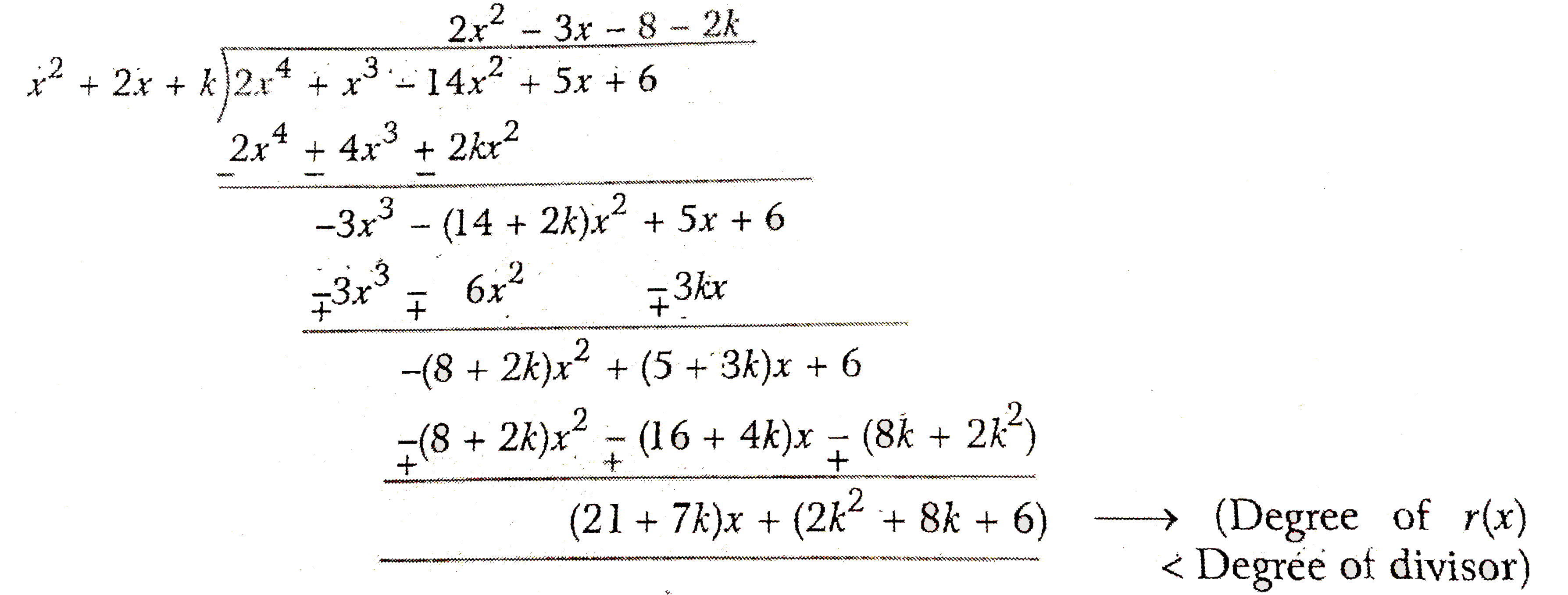 But remainder =0 `IMPLIES""(21+7k)x+(2k^(2)+8k+6)=0` `implies ""21+7k=0 ""and ""2k^(2)+8k+=0` `implies "" 7k=-21 "" and "" k^(2)+4k+3=0` `implies "" k=-3"" and ""(k+3)(k+1)=0` `implies "" k=-3 ""and ""k=-3 or k=-1` `:. "" k=-3` Now, `q(x)=2x^(2)-3x-8-2k=2x^(2)-3x-8+6=2x^(2)-3x-2` `=2x^(2)-4x+x-2=2x(x-2)+1(x-2)=(x-2)(2x+1)` Its zeroes are given by x-2=0 and 2x+1=0 `implies ""x=2 andx=-(1)/(2)` and `"" g(x)=x^(2)+2x+k=x^(2)+2x-3=x^(2)+3x-x-3` `=x(x+3)-1(x+3)=(x+3)(x-1)` Its zeroes are given by x+3=0 and x-1=0 `implies"" `x=-3 and x=1 `:.` Zeroes of g(x) are-3and 1 and zeroes of p(x) are -3, 1, 2 and `-(1)/(2) ""` Ans. |
|