InterviewSolution
Saved Bookmarks
| 1. |
From a point on the ground40 m away from the foot of a tower, the angle of elevation of the top of thetower is 30^(@). The angle of elevation of |
|
Answer» A be the towerpoint of observation. Then, `angleBAC = 30^(@), ANGLEBAD = 45^(@)`and `AB = 40 m`. From right `DeltaABD `, we have `(BD)/(AB) = tan 45^(@) = 1 RARR (BD)/(40 m) = 1 rArr BD = 40 m`. From right `DeltaABC`,we have `(BC)/(AB) = tan 30^(@) = 1/(sqrt(3)) rArr (BC)/(40 m)=1/(sqrt(3))`. `rArr BC = (40 m)/(sqrt(3)) rArr BC = (40 m)/(sqrt(3)) xx (sqrt(3))/(sqrt(3))= (40sqrt(3))/(3) m`. (i) HEIGHT of the tower `= BC = (40sqrt(3))/(3) m = 23.1 m` (ii) Deapth of tank`= CD = (BD - BC) = (40-23.1) m = 16.9 m`. 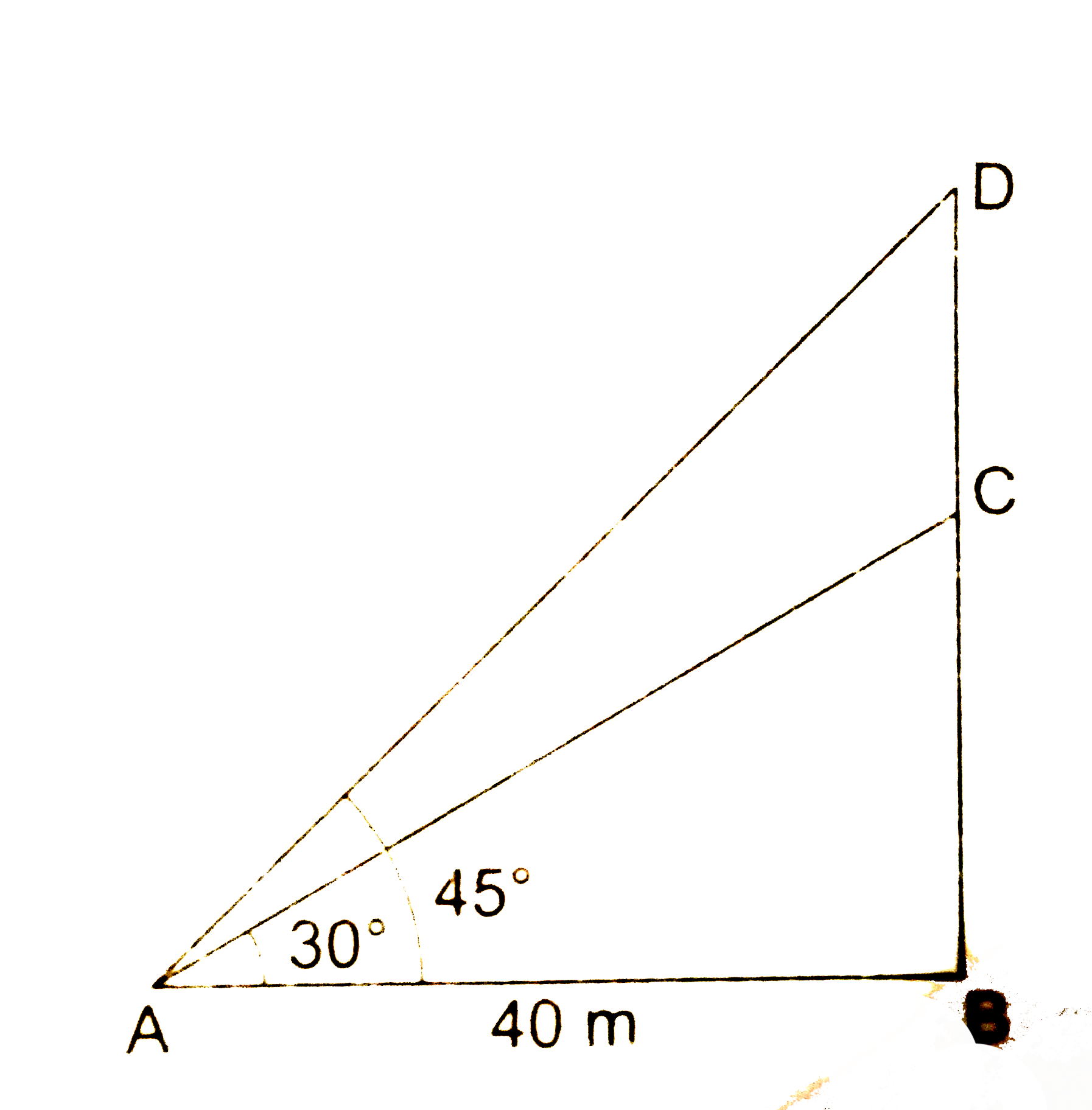
|
|