InterviewSolution
Saved Bookmarks
| 1. |
Point P (h,k) divides a line segment between the exes in the ratio 1:2 Find the lengths (intercepts) on the axes made by this segment. Also find the area of triangle formed by the line segment and the axes. |
|
Answer» Solution :Let AB be the line segment joining A (0.y) and B (x,0) between the axes. P (h,k) divides the line segment in the ratio `1:2.` Now, question arises that whether `PA:PB=1:2` or `PB:PA=1:2` or `PB:PA = 1:2` The answer of this is that always we take the FORMER part of ratio towards the X-axis and latter part of ratio towards the Y-axis. 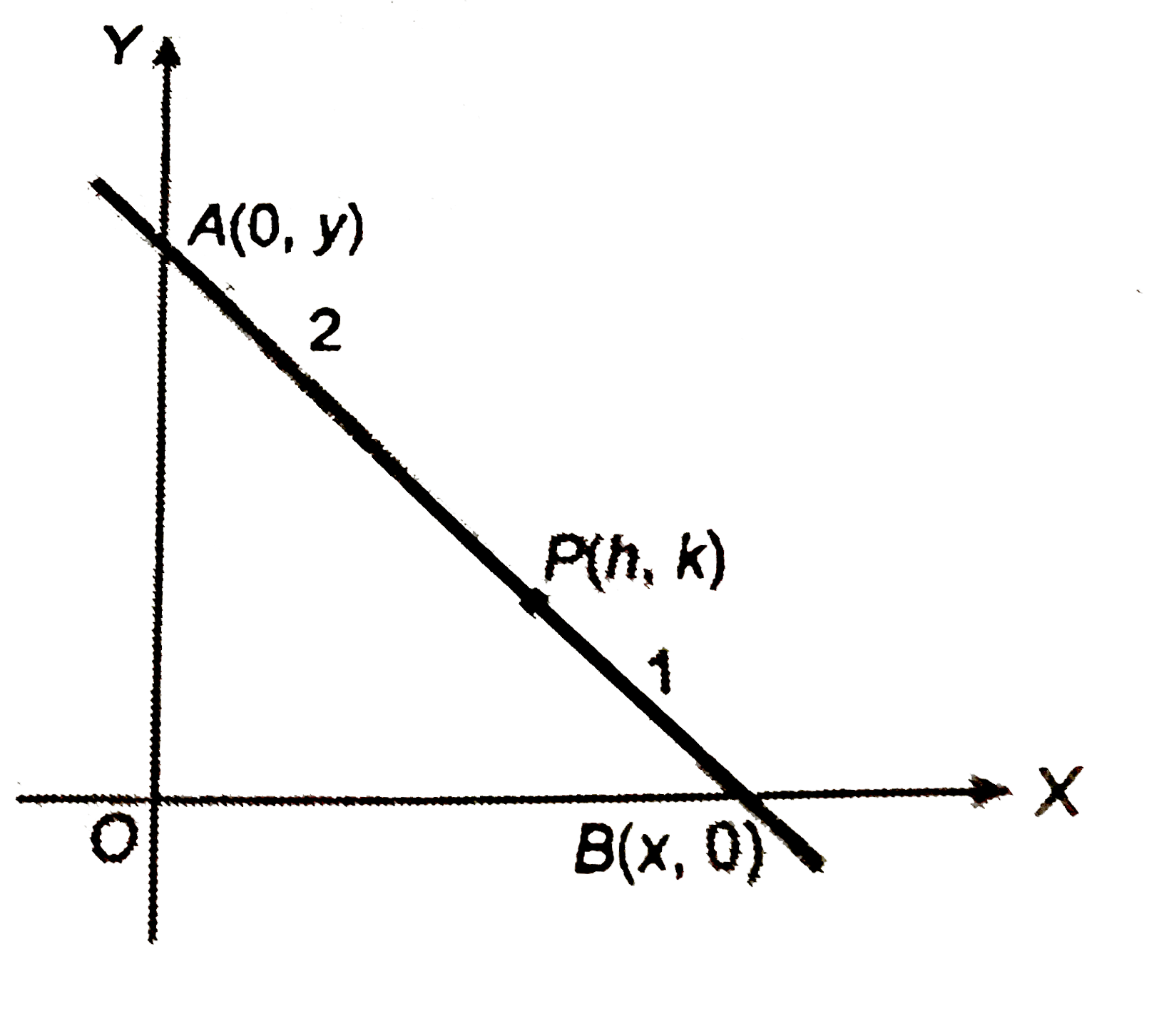 So, here we will take `""PB,PA=1:2` `THEREFORE` By using section FORMULA, `h=(1(0)+2(x))/(1+2)implies""h=(2x)/(3)impliesx=(3H)/(2)` and `k=(1(y)+2(0))/(1+2)implies""k=(y)/(3)impliesy=3k` So, length of intercept on the X-axis `=OB=x=(3h)/(2)` and the length of intercept on the Y-axis =OA = y = 3k. `therefore` Area of `DeltaAOB=1/2xxOBxxOA=1/2(3h)/(2)xx3k=9/4hk` SQUARE units |
|