InterviewSolution
Saved Bookmarks
| 1. |
Rahul an engieering student, prepared a model shaped like a cylinder with two cones attached at its ens. The diameter of the model is 3 cm and its length is 12 cm .If each conical part has a model (assume the oute and inner dimensions of the model to be nearly the same ),(ii) cost of painting the outer surface of the model at ₹ 12. 50 per cm^2 |
|
Answer» SOLUTION :Radius of each conical part `r = 3//2 cm ` Radius of CYLINDRICAL part , `r = 3//2 cm ` 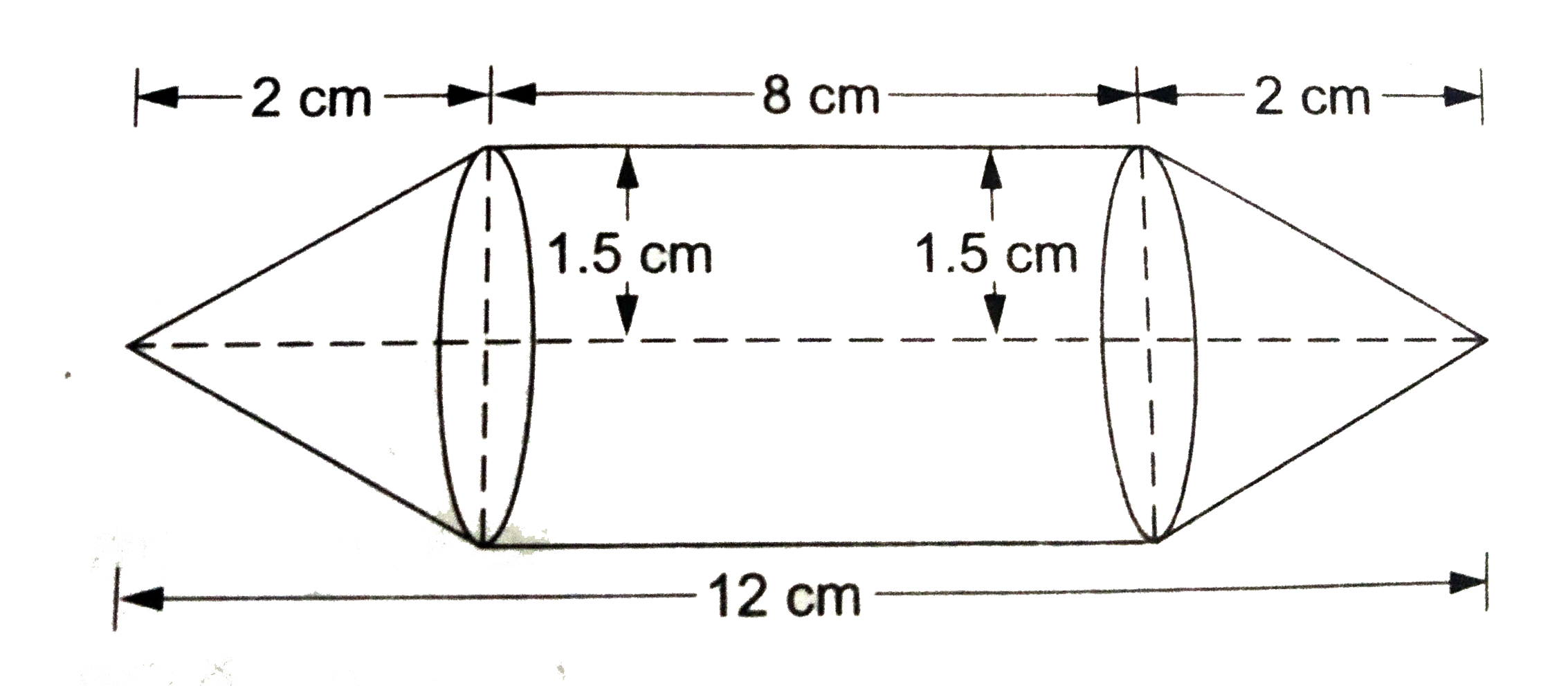 Height of each conical part, h=2cm Length of the cylinder part, `H= (12-2 xx 2 ) cm = 8 cm ` SLANT height of each conical part, `l= sqrt(r^2+ h^2)= sqrt((3/2)^2+2^2 cm = sqrt(9/4 + 4 ) cm ` `= sqrt(25/4) ` cm = 5/2 cm (i) Volume of air CONTAINED in the model = volume of 2 conical parts + volume of the cylindrical part `= 2 xx 1/3 pi r^2 h+ pi r^2H = pi r^2 (2/3 h+H)` `= [ 22/7 xx 3/2 xx 3/2 xx (2/3 xx 2 + 8 )] cm^3` `= (22/7 xx 3/2xx 3/2 xx 28/3)cm^2= 66 cm ^3` (ii) Total surface area of the model = curved SUFACE area of 2 conical parts + curved surface area of the cylindrical part `= 2 xx pirl + 2 pi r H = 2 pi rl (l+H)` `[2xx 22/7xx 3/2 xx (2.5 + 8)] cm^2` `= (2xx 22/7 xx 3/2 xx 10.5 ) cm^2 = 99 cm^2` `therefore` cost of painting the model = ₹` (99 xx 12.50) ` = ₹ 1237. 50 . |
|