InterviewSolution
Saved Bookmarks
| 1. |
Show that the following system of equations have unique solution :{:((i),7x-2y=3,(ii),3x+y=17,(iii),2x+5y=17,),(,22x-3y=16,,8x+11y = 37,,5x+3y=14,):}and also solve the system of equations in each case. |
|
Answer» Solution :(i) GIVEN equations are7x - 2y = 3 ….(1) 22x - 3y = 16 ….(2) Here, `a_(1) = 7, b_(1) = - 2`and `c_(1) = 3` [from (1)] `a_(22) = 22, b_(2) = - 3` and `c_(2) = 16`[from (2)] Now,`(a_(1))/(a_(2)) = (7)/(22)` and `(b_(1))/(b_(2)) = (-2)/(-3)=(2)/(3)` Since `(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`. HENCE, the given system has a unique solution. By cross multiplication method, we have 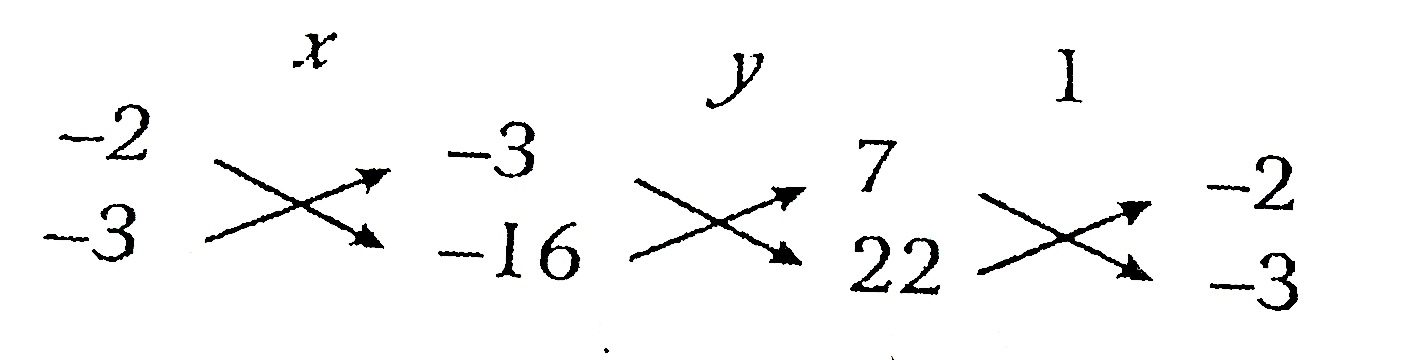 `(x)/((-2)xx(-16)-(-3)xx(-3))=(y)/((-3)xx22-(-16) xx7)=(1)/(7xx (-3) - 22 xx (-2))` `implies (x)/(32-9) = (y)/(-66 + 112) = (1)/(-21+44)` implies`(x)/(23) = (y)/(46) = (1)/(23)` When`(x)/(23) = (1)/(23) implies x = 1` and`(y)/(46) = (1)/(23) implies y = 2` Hence, `{:(x=1),(y=2):}}` is the required solution. (ii) The given system of equations is 3x + y = 17 ....(1) 8x + 11y = 37 ....(2) Here `a_(1) = 3, b_(1) = 1`and `c_(1) = 17`[from (1)] `a_(2) = 8, b_(2) = 11` and `c_(2) = 37` [from(2)] Now`(a_(1))/(a_(2)) = (3)/(8), (b_(1))/(b_(2)) = (1)/(11)` Since`(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`.Hence, the given system has a unique solution. We can write the equations as `3x + y - 17 = 0 and 8x + 11y - 37 = 0` By cross multiplication method, we have 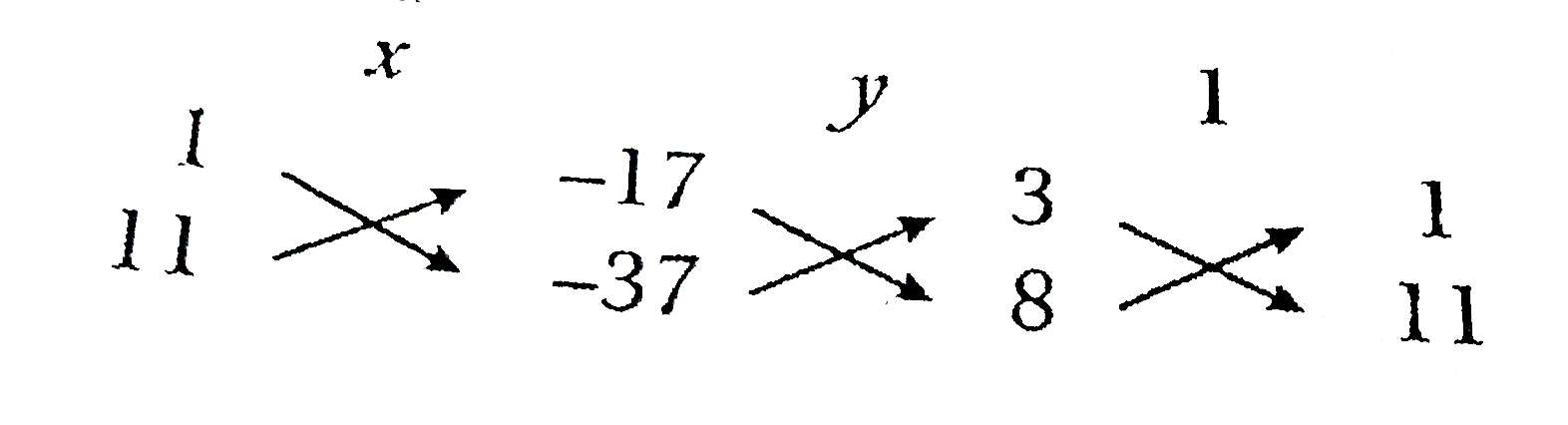 `(x)/(1xx(-37)-11xx(-17))=(y)/((-17)xx8-(-37)xx3)=(1)/(3xx11-8xx1)` implies`(x)/(150) = (y)/(-25) = (1)/(25)`When `(x)/(150) = (1)/(25) implies x = 6` and`(y)/(-25) = (1)/(25) implies y = - 1` Hence,`{:(x = 6),(y = -1):}}`is the required solution. (iii) The given system of equations is 2x + 5y - 17 = 0....(1) 5x + 3y - 14 = 0....(2) Here,`a_(1) = 2,b_(1) = 5` and `c_(1) = - 17`[from (1)] `a_(2) = 5, b_(2) = 3` and `c_(2) =- 14`[from (2)] Now,`(a_(1))/(a_(2))=(2)/(5), (b_(1))/(b_(2)) = (5)/(3)` Since`(a_(1))/(a_(2)) ne (b_(1))/(b_(2))`.Hence, the given systemof equations has a unique solution. By cross multiplication method, we have  `(x)/(5xx (-14)-3xx(-17))=(y)/((-17)xx5-(-14)xx2)=(1)/(2xx3-5xx5)` implies`(x)/(-70 + 51) = (y)/(-85 + 28) = (1)/(6-25)` implies`(x)/(-19) = (y)/(-57) = (1)/(-19)` impliesWhen`(x)/(-19) = (1)/(-19) implies x = 1` and`(y)/(-57) = (1)/(-19) implies y = 3` Hence,`{:(x = 1),(y = 3):}}` is the required solution. |
|