InterviewSolution
Saved Bookmarks
InterviewSolution
| 1. |
The radii of two concentric circles are 13cm and 8cm, AB is a diameter of bigger circle. BD is a tangent to the smaller circle touching it at D. Find the length AD. |
|
Answer» Solution :Produce BD to E which CUTS the circle at E. Join AE and OD. Since AB is the diameter of bigger circle. `:.""angleAEB=90^(@)""`(angle in a semicircle is right angle) ALSO, `angleODB=90^(@)""`(radius through point of contact is `_|_` to the tangent) Now, in `triangleBOD` and `triangleBAE` `angleB=ANGLEB""`(common) `angleODB=angleAEB""`(EACH `90^(@)`) `:.""triangleBOD~triangleBAE""`(AA corollary) `:.""(OD)/(AE)=(OB)/(AB)""`(corresponding sind of similar triangles are proportional) `implies""(8)/(AE)=(r)/(2r)""implies""AE=16cm` Since, `OD_|_EB` `:.""DE=DB""`(`_|_` drawn from the centre to the CHORD BISECTS the chord) In right `triangleODB,` `DB^(2)=OB^(2)-OD^(2)` `= (13)^(2)-(8)^(2)=169-64=105` `:.""DB=sqrt(105)cm=ED` Now, in right `triangleAED,` by Pythagoras theorem `AD^(2)=AE^(2)+ED^(2) ` `implies""AD^(2)=(16)^(2)+105=256+105=361` `implies""AD=sqrt(361)` i.e., `19 cm` Hence, `""AD=19cm.`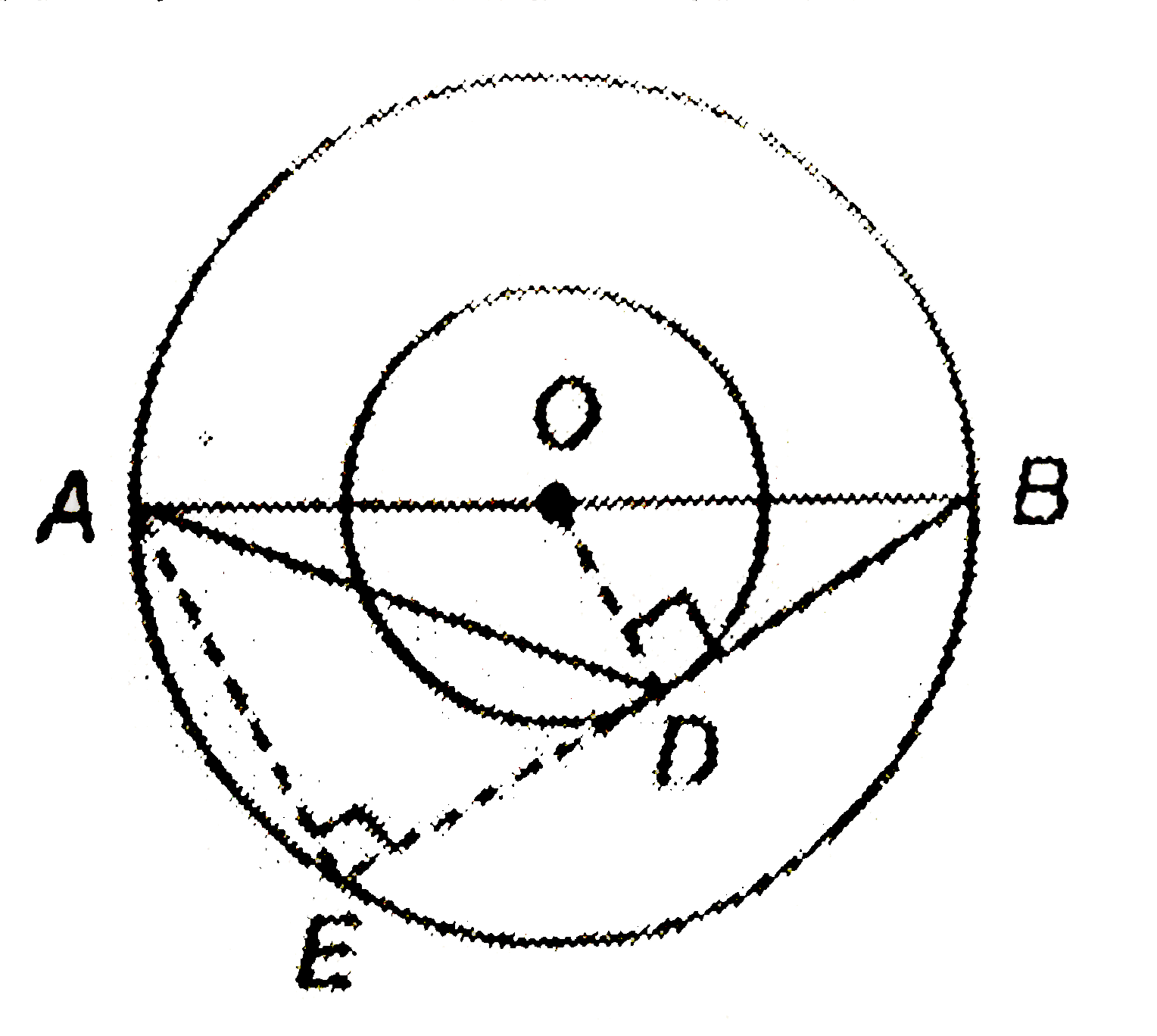 
|
|