Three mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?

Three mass points each of mass m are placed at the vertices of an equi

1.	Three mass points each of mass m are placed at the vertices of an equilateral tringale of side l. What is the gravitational field and potential due to three masses at the centroid of the triangle ?
Answer» Solution :`E_1= (GM)/((OA)^2)` `E_2= (GM)/((OB)^2)` `E_3= (GM)/((OC)^2)` 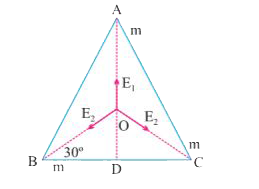From `triangleOBD, ""cos 30^(@)= (BD)/(OB)=(l"/"2)/(OB)` `OB= (l"/"2)/(cos 30^(@))= (BD)/(OB)= (l"/"2)/(2sqrt(3))= l"/"sqrt(3)` Gravitational field at O due to m at A, B and C is say `vec(E_1), vec(E_2)" and " vec(E_3)`. `E= sqrt(E_(2)^(2)+E_(3)^(2)+2E_(2)E_(3) cos 120^(@))` `=sqrt(((GM3)^2)/(I^2)+((3Gm)/(I))^2+2((3GM)/(I))(-(1)/(2)))` `=(3GM)/(I)=` along OD `vecE` is equal and opposite to `vec(E_1)` net gravitational field = zero As gravitational potential is scalar `V ""=V_(1)+V_(2)+V_(3)` `=(GM)/(OA)-(GM)/(OB)-(GM)/(OC)` `V""= -(3GM)/(I"/"sqrt(3))= -3sqrt(3)(Gm)/(I)`.