InterviewSolution
Saved Bookmarks
| 1. |
trianglePQR~trianglePMN."In" trianglePQR,PQ= 4 cm , QR = 5 cm and PR = 6 cm. Construct trianglePQR and trianglePMN such that (PR)/(PN)=5/3 |
|
Answer» Solution :Analysis : The length of three sides of `TRIANGLEPQR` are known `therefore trianglePQR`can be constructed. `triangle PQR~trianglePMN" such that "(PR)/(PN)=5/3` `therefore` sides of trianglePMN are smaller than the corresponding sides of `trianglePQR and angleQRP~=angleMPN""...("Corresponding angles of similar triangles")` `therefore trianglePQR and trianglePMN` can have common angle P.  Consider the given ANALYTICAL figure If we divide Pr into 5 equal parts, then PN would be equal to three equal parts. Thus POINT N can be located on seg PR. As, `anglePRQ~=anglePNM""...("Corresponding angles of similar triangles")` `therefore` at point N, we draw line NM || side QR intersectiong side PQ at M. Thus we obtain `trianglePMN` Stepas of construction : (1) CONSTRUCT `trianglePQR` such that PQ = 4 cm , PR = 6 cm and QR = 5cm (2) Divide segment PR in 5 equal parts Name the endpoint of the third part as N. (4) Now, draw a line parallel to QR through N. Mark the point of intersection of the parallel line with PQ as M. (5) `triangle PMN` is required triangle similar to `trianglePQR` construction : 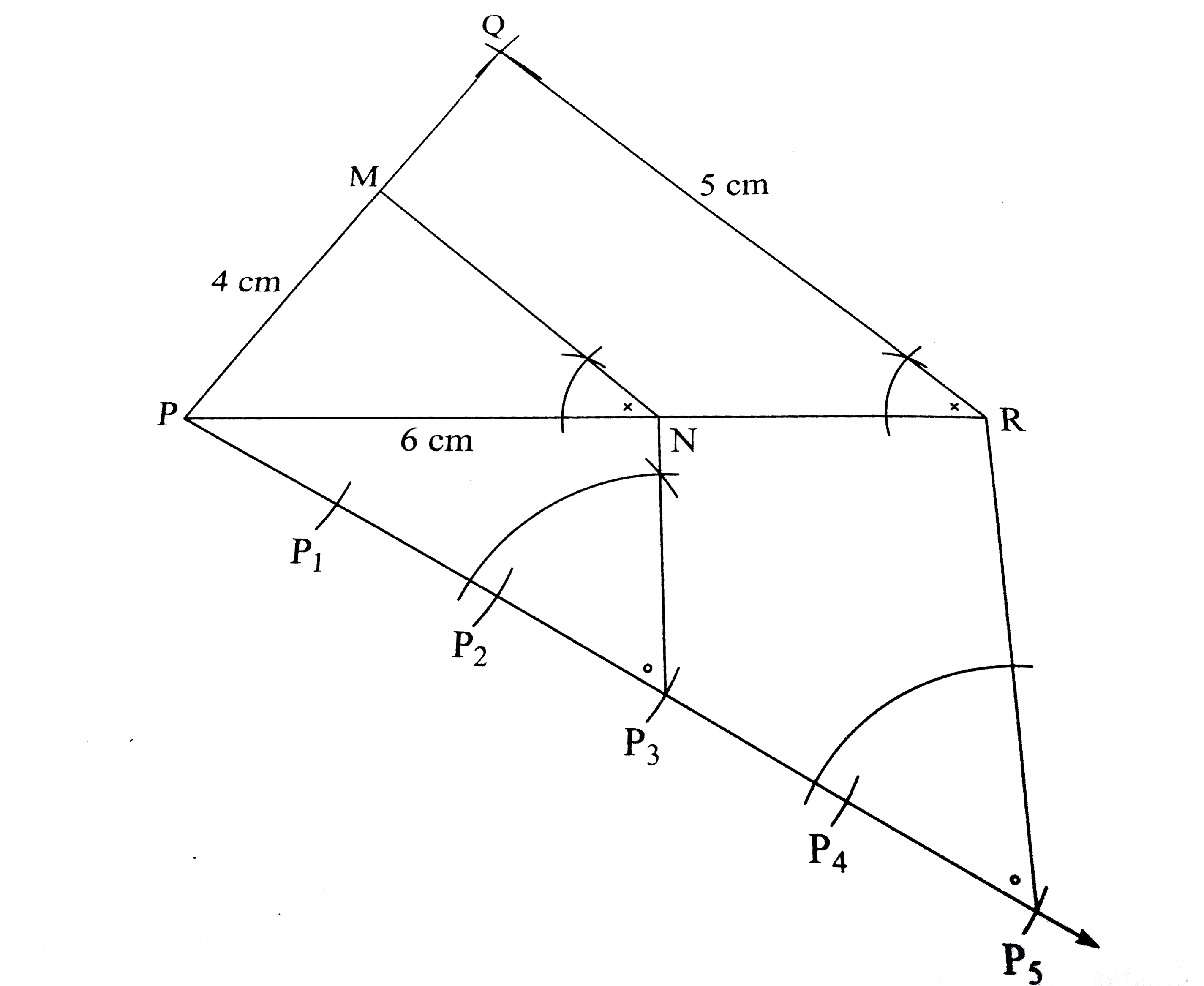
|
|